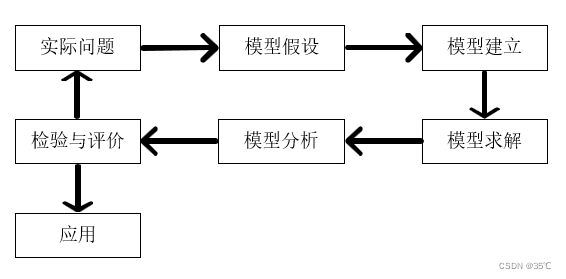
当需要从定量的角度分析和研究一个实际问题时，就要在深入调查研究、了解对象信息、做出简化假设、分析内在规律等工作的基础上，用数学的符号和语言进行表述来建立数学模型。数学建模就是通过计算得到的结果来解释实际问题，并接受实际的检验，来建立数学模型的过程。

通常数学建模的定义为：关于部分现实世界和为一种特殊目的而做的一个抽象的、简化的结构。

具体来说。数学模型就是为了某种目的，用字母、数学及其他数学符号建立起来的等式或不等式以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式。

数学是在实际应用的需求中产生的，要解决实际问题就必须建立数学模型，从此意义上讲数学建模和数学一样有古老的历史。

数学以空前的广度和深度向其他科学技术领域渗透，以往较少应用数学的领域现在也迅速走向定量化、数量化，需要建立大量数学模型。特别是新技术、新工艺蓬勃兴起，计算机的普及和广泛应用，数学在许多高新技术上起着十分关键的作用。

关注公众号，学习数模，领取免费资源。