第二章SCAAR机器人的机械结构设计
近年来，工业机器人有一个发展趋势:机械结构模块化和可重构化。例如关节模块中的伺服电机、减速机、检测系统三位一体化;由关节模块、连杆模块用重组方式构造机器人整机;国外己有模块化装配机器人产品问市。本章介绍模块化的设计方法在SCARA机器人的结构设计中的应用。

2.1 SCARA机器人的总体设计
2.1.1 SCARA机器人的技术参数
(1) 抓重：≤1kg
(2) 自由度：4
(3) 运动参数：
大臂：±100。(回转角度)，角速度≤1.8rad/s
小臂：±50。(回转角度)，角速度≤1.8rad /s
手腕回转：±100。(回转角度)，角速度≤1.8rad。/s
手腕升降：100mm(升降距离)，线速度≤0.01m/s
2.1.2 SCARA机器人外形尺寸与工作空间
依据设计要求，SCARA机器人的外形尺寸如图2一1所示，工作空间如图2一2。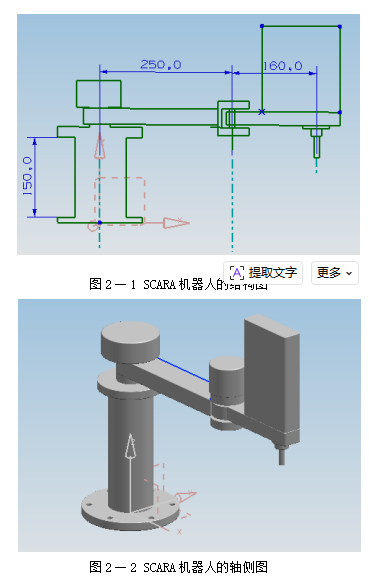
2.1.3 SCARA机器人的总体传动方案
目前，机器人的传动系统中主要是使用VR减速器或谐波减速器。VR减速器是近几年发展起来的以两级减速和中心圆盘支撑为主的全封闭式摆线针轮减速器，与其它减速方式相比，VR减速器具有减速比大、同轴线传动、传动精度高、刚度大、结构紧凑等优点，适用于重载、高速和高精度场合。谐波减速器也具有传动比大，承载能力大，传动精度高，传动平稳，传动效率高，结构简单、体积小，重量轻等优点，而且相对于VR减速器而一言，其制造成本要低很多，所以在本设计中采用谐波减速机。SCARA机器人大小臂均要承受轴向压力和倾覆力矩，所以大臂和小臂均采用谐波减速机加推力向心交叉短圆柱滚子轴承结构。而推力向心交叉短圆柱滚子轴承刚度高，能承受轴向压力与径向扭矩，与谐波减速机配合正符合SCAAR机器人大小臂高刚性及高的抗倾覆力矩的要求。这样有利于缩短传动链，简化结构设计〔伙，。由于主轴处于机器人小臂末端，相对线速度大，对重量与惯量特别敏感，所以传动方式要求同时实现Z轴方向直线运动和绕Z轴的回转运动，并要求结构紧凑、重量轻。经过比较，选择同步齿形带加滚珠丝杠来实现Z轴上下运动，而用同步齿形带加带键的滑动轴套来实现Z轴旋转运动。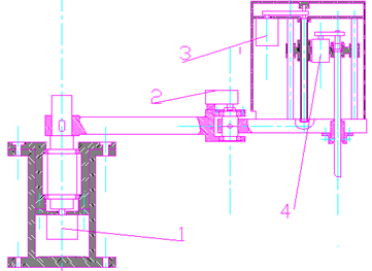

大臂回转:步进电机1一>谐波减速器一>大臂
小臂回转:步进电机2一>谐波减速器一>小臂
主轴垂直直线运动:步进电机3一>同步齿形带一>丝杠螺母一>主轴
主轴旋转:步进电机4一>同步齿形带一>花键一>主轴
2.2机器人关键零部件设计计算
2.2.1减速机的设计计算
大臂的转动速度为角速度≤1.8rad/s，电机初选四通步进电机，两相混合式86BYG250B一0402。最高转速为30OORPM，设计电机按1500RPM工作，则: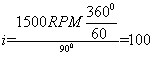
初选谐波减速器为北京中技克美谐波传动有限责任公司的机型为60的XB3扁平
型谐波减速器，其传动比可以是100(XB3一60系列组件的规格和额定数值见下表)
表2一2XB3一60一100的规格和额定数值表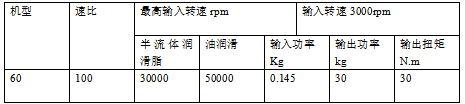

第三章SCARA机器人的位姿误差建模

设计一个开放式的机器人系统，其中关键技术之一就是对相应的机器人本体的运动学进行分析并建立相应的运动学模型。本章系统地描述了平面关节型ScARA机器人的运动学和位姿误差模型的建立。在Denavit一Hartenberg参数法建立的机器人末端位姿变换方程的基础上，利用机构通用精度算法建立了机器人末端位姿误差模型。通过矩阵运算，建立了机器人末端位姿误差与各杆件运动学参数误差之间的函数关系式。用此方法建立的误差模型进行误差标定和补偿，可以提高机器人的定位精度。这对开发开放式机器人系统有重要的参考价值。

3.1基于机构精度通用算法的机器人位姿误差建模
机器人位姿误差建模方法归纳为矩阵法和矢量法两大类型，其中矢量法又分为矢量分析及螺旋变换法和摄动法，运用精度平衡方程式和回转变换张量方法等【2】【5】机器人运动学Denvait一Hartenberg参数法坐标变换中坐标变换矩阵A，及手臂变换矩阵笋都是不考虑各运动学参数误差的理想变换，但实际应用中，无论机器人制造精度多高，都会由于各种原因引起机器人运动学参数误差，影响
机构通用精度算法是一种既不需要求导也不需要建立机构传动方程的通用算法，具有通用性广，计算量小和精确度高等优点，由于其算法模型与前面所建立的机器人位姿变换模型正好适合，因此，利用这种算法建立机器人位姿误通用精度算法基本思路是:任何具有精度要求的机构系统是一个有机联系差模型。
整体，如果系统构件中有原始误差存在，必然要影响从动件运动轨迹，从而产生机构位置误差，而任何原始误差影响均可视为构件本身坐标系产生微小转动或移动，至于机械系统精度通用数学模型可以应用空间坐标变换原理，并通过所对应的构件运动变换矩阵与位置误差矩阵连乘叠加来表达。通用精度算法的坐标变换推导过程完全类似于机器人坐标变换坐标推导过程，这里不再叙述，仅给出其结论，并将其结论进行整理变化后应用于机器人位姿误差计算，建立机器人位姿误差变换模型

3.2机构精度通用算法
设某个机构由n个运动构件和一个固定构件组成，若将起始坐标系S。建立在固定构件上，坐标系S，建立在运动构件(ii=，2l，…n)上。运动构件n的坐标系凡，为目标坐标系。坐标系又_，与s;间变换矩阵为A，，以向量价二x(，y，习)(与机器人齐次变换矩阵规定一样)表示点P在坐标系s，中位置，则由坐标间位姿变换可知目标坐标系况，中某点P在各坐标系S，中的向量乙，应有如下关系式: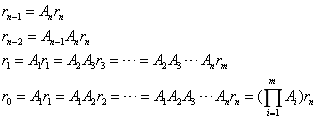
3.2.2机器人位姿误差模型的建立
用及分别代表连杆i的理想变换矩阵和实际变换矩阵，代表理想变换矩阵和实际变换矩阵之差，则考虑误差影响时相邻坐标系的真实变换矩阵为: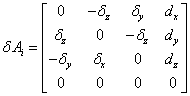

（3.2.8）
设没有误差时，杆件i坐标系变换后的坐标系为，类似公式(3.2.4)推导过程，由于存在若干种误差，坐标系又进行一次变换，变成坐标系，这时坐标系相对存在位姿误差即原点在坐标系为其三个坐标轴相对的三个坐标轴分别有偏转角由公式(.3.22)可得坐标系相对的变换矩阵为。