多目标点路径规划——蚁群+A*算法 室内旅行商问题——送餐移动机器人（从厨房出发到达多个目标点，最后返回厨房） 1，A*算法规划两两之间的路径，并计算路径长度； 2，蚁群算法依据两点之间路径长度，规划多个目标点的先后到达顺序； 3，组合最优顺序的路径，输出最后路线

最近一直在研究室内旅行商问题，也就是送餐移动机器人从厨房出发到达多个目标点，最后返回厨房的路径规划。今天就来和大家分享一下我用蚁群 + A* 算法解决这个问题的过程😃

A* 算法规划两两之间的路径，并计算路径长度

A* 算法是一种常用的启发式搜索算法，在路径规划中表现出色。它通过一个评估函数来选择下一个扩展的节点，这个评估函数结合了从起点到当前节点的实际代价 g(n) 和从当前节点到目标节点的估计代价 h(n)，即 f(n) = g(n) + h(n)。

下面是一段简化的 Python 代码来实现 A* 算法规划两点之间的路径：

import heapq

def astar(graph, start, end):
    open_set = []
    heapq.heappush(open_set, (0, start))
    came_from = {}
    g_score = {node: float('inf') for node in graph}
    g_score[start] = 0
    f_score = {node: float('inf') for node in graph}
    f_score[start] = heuristic(start, end)

    while open_set:
        _, current = heapq.heappop(open_set)

        if current == end:
            path = reconstruct_path(came_from, current)
            length = calculate_path_length(path)
            return path, length

        for neighbor in graph[current].keys():
            tentative_g_score = g_score[current] + graph[current][neighbor]

            if tentative_g_score < g_score[neighbor]:
                came_from[neighbor] = current
                g_score[neighbor] = tentative_g_score
                f_score[neighbor] = tentative_g_score + heuristic(neighbor, end)
                if neighbor not in [i[1] for i in open_set]:
                    heapq.heappush(open_set, (f_score[neighbor], neighbor))

def heuristic(a, b):
    # 这里简单用曼哈顿距离作为启发函数
    return abs(a[0] - b[0]) + abs(a[1] - b[1])

def reconstruct_path(came_from, current):
    total_path = [current]
    while current in came_from:
        current = came_from[current]
        total_path.insert(0, current)
    return total_path

def calculate_path_length(path):
    length = 0
    for i in range(len(path) - 1):
        length += graph[path[i]][path[i + 1]]
    return length

代码分析：

1. 首先定义了一些初始的数据结构，如 openset 用于存储待扩展的节点，camefrom 记录每个节点的前驱节点，gscore 记录从起点到每个节点的实际代价，fscore 记录评估函数的值。
2. 在 while 循环中，每次从 openset 中取出 fscore 最小的节点进行扩展。
3. 对于每个扩展的节点，检查其邻居节点，计算从起点经过当前节点到邻居节点的 tentativegscore，如果小于邻居节点当前的 gscore，则更新 camefrom、gscore 和 fscore，并将邻居节点加入 open_set。
4. 当扩展到目标节点时，通过 reconstruct_path 函数重建路径，并计算路径长度。

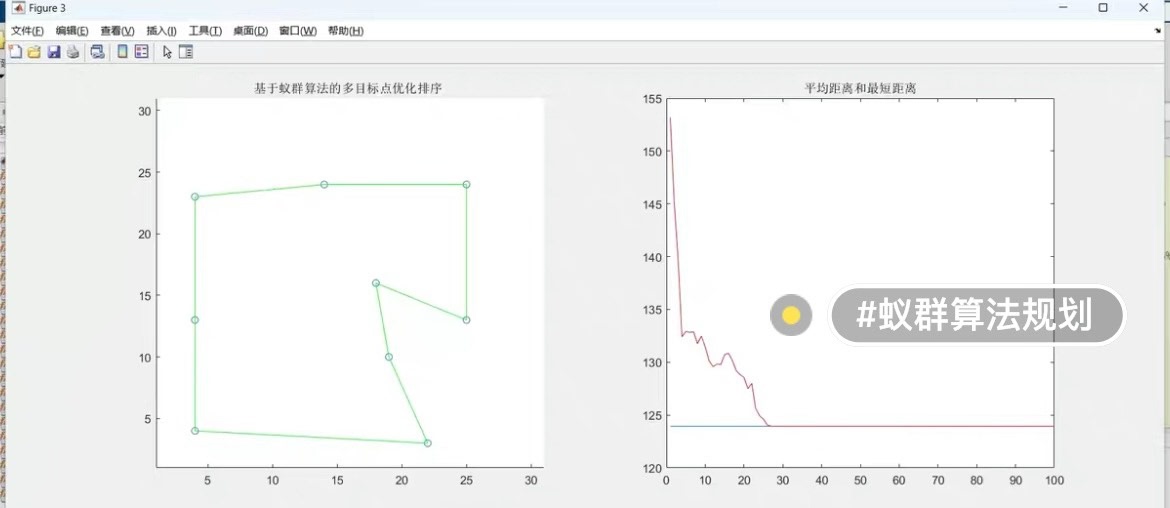
蚁群算法依据两点之间路径长度，规划多个目标点的先后到达顺序

蚁群算法是一种基于群体智能的优化算法，它模拟蚂蚁觅食的行为来寻找最优路径。在我们的问题中，蚂蚁会根据两点之间路径长度来选择下一个目标点。

import random

def ant_colony(points, num_ants, num_iterations, alpha, beta, rho):
    num_points = len(points)
    distances = [[astar(graph, points[i], points[j])[1] for j in range(num_points)] for i in range(num_points)]
    pheromone = [[1.0 for _ in range(num_points)] for _ in range(num_points)]

    best_order = None
    best_distance = float('inf')

    for _ in range(num_iterations):
        for _ in range(num_ants):
            order = [0]
            unvisited = set(range(1, num_points))
            current = 0

            while unvisited:
                next_point = select_next_point(pheromone[current], distances[current], unvisited, alpha, beta)
                order.append(next_point)
                unvisited.remove(next_point)
                current = next_point

            order.append(0)  # 回到起点
            distance = calculate_total_distance(order, distances)

            if distance < best_distance:
                best_distance = distance
                best_order = order[:]

            update_pheromone(pheromone, order, distance, rho)

    return best_order, best_distance

def select_next_point(pheromone, distances, unvisited, alpha, beta):
    numerators = [pheromone[i] ** alpha * (1.0 / distances[i]) ** beta for i in unvisited]
    denominator = sum(numerators)
    probabilities = [num / denominator for num in numerators]
    return random.choices(list(unvisited), weights=probabilities)[0]

def calculate_total_distance(order, distances):
    total_distance = 0
    for i in range(len(order) - 1):
        total_distance += distances[order[i]][order[i + 1]]
    return total_distance

def update_pheromone(pheromone, order, distance, rho):
    for i in range(len(order) - 1):
        pheromone[order[i]][order[i + 1]] = (1 - rho) * pheromone[order[i]][order[i + 1]] + 1.0 / distance
        pheromone[order[i + 1]][order[i]] = pheromone[order[i]][order[i + 1]]

代码分析：

1. 首先计算所有点之间的距离矩阵 distances 和初始的信息素矩阵 pheromone。
2. 在每次迭代中，每只蚂蚁从起点出发，根据信息素和距离选择下一个目标点，直到遍历完所有目标点后回到起点。
3. 计算每只蚂蚁走过的路径总长度，更新最优路径和最优距离。
4. 根据蚂蚁走过的路径长度更新信息素矩阵，信息素会随着时间逐渐挥发（通过 rho 参数控制），同时在走过的路径上增加信息素。

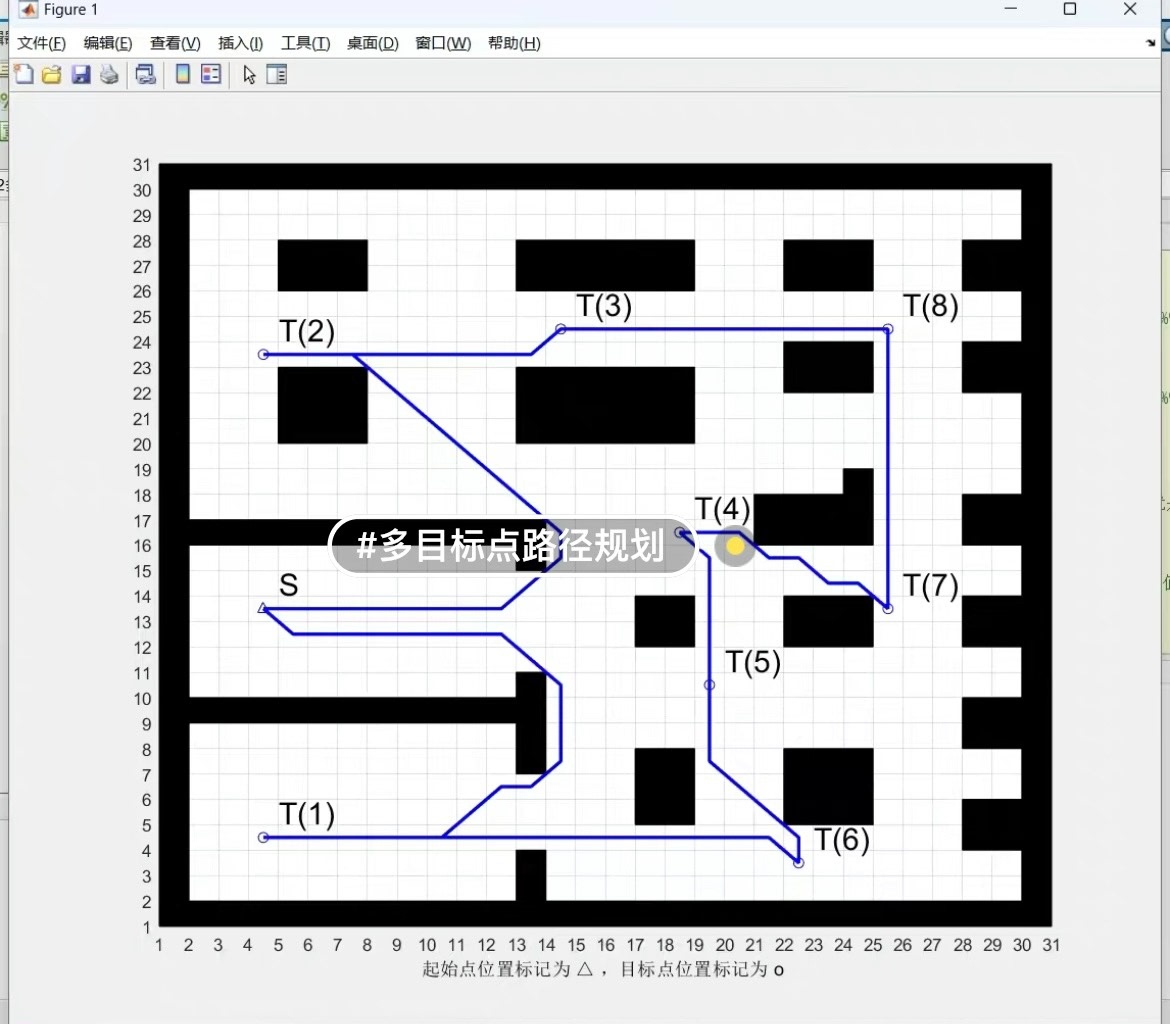
组合最优顺序的路径，输出最后路线

最后，我们将蚁群算法得到的目标点最优顺序与 A* 算法规划的两两之间路径进行组合，得到最终的路线。

def combine_paths(best_order, points):
    final_route = [points[0]]
    for i in range(len(best_order) - 1):
        start = points[best_order[i]]
        end = points[best_order[i + 1]]
        path, _ = astar(graph, start, end)
        final_route.extend(path[1:])
    final_route.append(points[0])  # 回到起点
    return final_route

代码分析：

1. 从起点开始，依次根据最优顺序，利用 A* 算法规划相邻目标点之间的路径，并将路径上的点加入最终路线，最后回到起点。

通过以上三个步骤，我们成功地用蚁群 + A* 算法解决了室内旅行商问题，为送餐移动机器人规划出了最优的路径😎。希望这篇分享对大家理解和实现类似的路径规划问题有所帮助！

这里假设 graph 是一个表示地图的邻接矩阵，存储了各个点之间的连接关系和距离信息。实际应用中需要根据具体的地图数据来构建这个 graph。

多目标点路径规划——蚁群+A*算法 室内旅行商问题——送餐移动机器人（从厨房出发到达多个目标点，最后返回厨房） 1，A*算法规划两两之间的路径，并计算路径长度； 2，蚁群算法依据两点之间路径长度，规划多个目标点的先后到达顺序； 3，组合最优顺序的路径，输出最后路线

以上代码只是一个简单的示例，实际应用中可能需要根据具体需求进行更多的优化和调整。比如，对于大规模的地图数据，可能需要考虑空间复杂度和时间复杂度的优化；对于启发函数的选择，也可以根据实际情况进行调整以提高算法的效率。

总之，多目标点路径规划是一个很有趣也很有挑战性的问题，通过蚁群算法和 A* 算法的结合，我们能够找到相对较优的解决方案。大家如果有什么想法或者问题，欢迎一起讨论呀😄

以上就是整个多目标点路径规划的实现过程啦，希望能给大家一些启发~

#路径规划 #蚁群算法 #A*算法 #室内旅行商问题