轮式移动机器人轨迹跟踪的MATHLAB程序，运用运动学和动力学模型的双闭环控制，借鉴自抗扰控制技术结合了非线性ESO，跟踪效果良好，控制和抗扰效果较优，可分享控制结构图。 这段程序主要是一个小车的动力学仿真程序，用于模拟小车在参考轨迹下的运动。下面我将对程序进行详细的分析解释。 首先，程序开始时使用`clear`、`clc`和`close all`命令来清除工作空间、命令窗口和图形窗口中的内容。 接下来，程序定义了一系列参数和变量，用于设置仿真的参数和存储仿真过程中的数据。这些参数包括小车的质量、车宽、驱动轮半径等，还有参考轨迹的振幅和频率，仿真步长，仿真时间等。 然后，程序定义了一些元胞数组，用于存储不同阶段的数据。这些数组包括参考轨迹位姿、真实运动轨迹位姿、参考轨迹一阶导数、虚拟参考轨迹速度、期望速度、真实速度、控制器输出的控制力矩、控制输入、期望速度与真实速度误差、摩擦值、外界扰动值、总扰动、位姿跟踪误差、扰动观测值等。 接下来，程序给这些变量赋初始值，包括小车的初始位姿和速度，虚拟初始速度，期望初始速度，控制器输出的控制力矩，扰动观测值等。 然后，程序进入一个循环，仿真时间从0到给定的仿真时间tf。在每个循环中，程序根据给定的参考轨迹生成圆形参考轨迹，并计算参考轨迹的一阶导数和虚拟参考轨迹速度。 接下来，程序计算位姿误差，并使用运动学控制器计算期望速度。然后，程序使用非线性ESO（Extended State Observer）估计速度扰动，并使用动力学控制器计算控制力矩。最后，程序根据控制力矩和扰动计算小车的实际速度和位姿，并计算位姿跟踪误差。 在每个循环结束时，程序更新时间和循环索引，并继续下一次循环，直到仿真时间达到设定的结束时间tf。 最后，程序绘制了多个图形来展示仿真结果。这些图形包括参考轨迹和实际运动轨迹的图像、参考轨迹角度和实际角度的图像、内环速度误差的图像、位姿跟踪误差的图像、线速度扰动和观测器估计的图像、角速度扰动和观测器估计的图像、速度曲线的图像和控制量输入的图像。 通过这些图形，可以直观地了解小车在参考轨迹下的运动情况，以及控制器的性能和位姿跟踪误差等。 这段程序涉及到的知识点包括动力学方程、参考轨迹生成、运动学控制器、非线性ESO、动力学控制器等。它主要用于解决小车在给定参考轨迹下的运动控制问题，通过控制器输出的控制力矩来控制小车的速度和位姿，以实现对参考轨迹的跟踪。

1. 系统概述

本文分析了一个轮式移动机器人轨迹跟踪控制的MATLAB仿真程序。该系统采用双闭环控制结构，结合了运动学控制器和动力学控制器，并引入了非线性扩张状态观测器（ESO） 来估计和补偿系统中的总扰动。该控制方案借鉴了自抗扰控制技术的思想，在存在摩擦力和外部扰动的情况下，实现了对参考轨迹的精确跟踪。

2. 控制系统架构

2.1 双闭环控制结构

系统采用分层控制策略：

• 外环（运动学控制层）：处理位姿跟踪误差，生成期望的速度指令
• 内环（动力学控制层）：实现速度跟踪，输出控制力矩

2.2 非线性ESO设计

系统设计了非线性扩张状态观测器，用于实时估计和补偿系统中的总扰动，包括摩擦力和外部扰动，这是保证系统鲁棒性的关键。

3. 核心算法实现

3.1 系统建模

机器人动力学方程简化为：

M_ba*V_dot + Vm_ba*V + F_ba + tau_d_ba = tau_ba

其中：

• M_ba为系统惯性矩阵
• F_ba为摩擦力项
• taudba为外部扰动
• tau_ba为控制力矩

3.2 轨迹生成模块

系统支持圆形参考轨迹生成：

q_r{1}(1:3,k) = [A*cos(omega*to); A*sin(omega*to); omega*to+pi/2];

3.3 坐标变换与误差计算

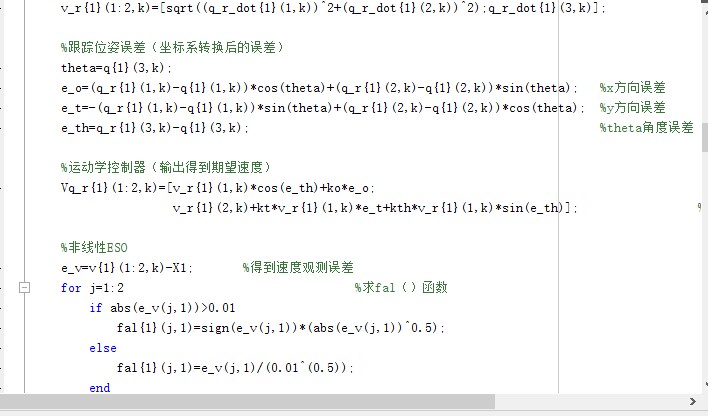
将全局坐标系下的跟踪误差转换到机器人本体坐标系：

theta = q{1}(3,k);
e_o = (q_r{1}(1,k)-q{1}(1,k))*cos(theta) + (q_r{1}(2,k)-q{1}(2,k))*sin(theta);
e_t = -(q_r{1}(1,k)-q{1}(1,k))*sin(theta) + (q_r{1}(2,k)-q{1}(2,k))*cos(theta);
e_th = q_r{1}(3,k)-q{1}(3,k);

3.4 运动学控制器

基于转换后的误差计算期望速度：

Vq_r{1}(1:2,k) = [v_r{1}(1,k)*cos(e_th) + ko*e_o;
                  v_r{1}(2,k) + kt*v_r{1}(1,k)*e_t + kth*v_r{1}(1,k)*sin(e_th)];

3.5 非线性ESO实现

ESO通过非线性函数处理观测误差，实现扰动的精确估计：

% 非线性fal函数
if abs(e_v(j,1)) > 0.01
    fal{1}(j,1) = sign(e_v(j,1))*(abs(e_v(j,1))^0.5);
else
    fal{1}(j,1) = e_v(j,1)/(0.01^(0.5));
end

% ESO状态更新
X1 = X1 + h*(X2 - zo*e_v + U{1}(1:2,k-1));
X2 = X2 - h*zt*fal{1}(1:2,1);
X3{1}(1:2,k) = -M_ba*X2;  % 扰动观测值

3.6 动力学控制器

结合ESO的扰动估计和速度误差反馈，计算控制力矩：

ec{1}(1:2,k) = Vq_r{1}(1:2,k) - v{1}(1:2,k);
tau_ba{1}(1:2,k) = X2 + Kf*ec{1}(1:2,k);
U{1}(1:2,k) = inv(M_ba)*tau_ba{1}(1:2,k);

4. 系统仿真与性能分析

程序提供了全面的可视化分析，包括：

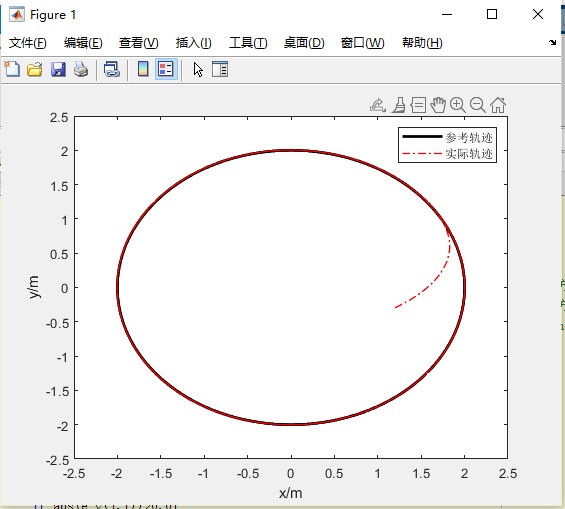
1. 轨迹跟踪效果：实际轨迹与参考轨迹的对比
2. 角度跟踪：方向角的跟踪性能
3. 速度误差：内环线速度和角速度的跟踪误差
4. 位姿误差：x、y方向和角度的跟踪误差
5. 扰动观测：ESO对系统扰动的估计效果
6. 速度曲线：虚拟、期望和实际速度的对比
7. 控制输入：控制器输出的控制量

5. 技术特点与优势

5.1 抗扰动性能

通过非线性ESO实时估计并补偿系统总扰动，显著提高了系统在存在摩擦和外部干扰情况下的鲁棒性。

5.2 双闭环设计优势

• 运动学外环：保证位姿跟踪精度
• 动力学内环：实现快速速度响应
• 解耦设计：简化控制器设计复杂度

5.3 非线性处理能力

采用非线性函数处理观测误差，增强了ESO在较大误差范围内的估计性能。

6. 应用价值

该控制方案适用于各类轮式移动机器人的轨迹跟踪任务，特别在以下场景中表现优异：

• 存在未知扰动的工作环境
• 需要高精度轨迹跟踪的应用
• 系统参数变化较大的情况

仿真结果表明，该控制策略能够有效抑制扰动影响，实现平滑、精确的轨迹跟踪，为实际轮式机器人控制系统设计提供了可靠的理论基础和实践参考。

轮式移动机器人轨迹跟踪的MATHLAB程序，运用运动学和动力学模型的双闭环控制，借鉴自抗扰控制技术结合了非线性ESO，跟踪效果良好，控制和抗扰效果较优，可分享控制结构图。 这段程序主要是一个小车的动力学仿真程序，用于模拟小车在参考轨迹下的运动。下面我将对程序进行详细的分析解释。 首先，程序开始时使用`clear`、`clc`和`close all`命令来清除工作空间、命令窗口和图形窗口中的内容。 接下来，程序定义了一系列参数和变量，用于设置仿真的参数和存储仿真过程中的数据。这些参数包括小车的质量、车宽、驱动轮半径等，还有参考轨迹的振幅和频率，仿真步长，仿真时间等。 然后，程序定义了一些元胞数组，用于存储不同阶段的数据。这些数组包括参考轨迹位姿、真实运动轨迹位姿、参考轨迹一阶导数、虚拟参考轨迹速度、期望速度、真实速度、控制器输出的控制力矩、控制输入、期望速度与真实速度误差、摩擦值、外界扰动值、总扰动、位姿跟踪误差、扰动观测值等。 接下来，程序给这些变量赋初始值，包括小车的初始位姿和速度，虚拟初始速度，期望初始速度，控制器输出的控制力矩，扰动观测值等。 然后，程序进入一个循环，仿真时间从0到给定的仿真时间tf。在每个循环中，程序根据给定的参考轨迹生成圆形参考轨迹，并计算参考轨迹的一阶导数和虚拟参考轨迹速度。 接下来，程序计算位姿误差，并使用运动学控制器计算期望速度。然后，程序使用非线性ESO（Extended State Observer）估计速度扰动，并使用动力学控制器计算控制力矩。最后，程序根据控制力矩和扰动计算小车的实际速度和位姿，并计算位姿跟踪误差。 在每个循环结束时，程序更新时间和循环索引，并继续下一次循环，直到仿真时间达到设定的结束时间tf。 最后，程序绘制了多个图形来展示仿真结果。这些图形包括参考轨迹和实际运动轨迹的图像、参考轨迹角度和实际角度的图像、内环速度误差的图像、位姿跟踪误差的图像、线速度扰动和观测器估计的图像、角速度扰动和观测器估计的图像、速度曲线的图像和控制量输入的图像。 通过这些图形，可以直观地了解小车在参考轨迹下的运动情况，以及控制器的性能和位姿跟踪误差等。 这段程序涉及到的知识点包括动力学方程、参考轨迹生成、运动学控制器、非线性ESO、动力学控制器等。它主要用于解决小车在给定参考轨迹下的运动控制问题，通过控制器输出的控制力矩来控制小车的速度和位姿，以实现对参考轨迹的跟踪。

通过调整控制器参数和观测器参数，该方案可以进一步优化以适应不同的应用需求和性能指标，展现了良好的工程应用前景。