2自由度机械臂轨迹跟踪控制，6自由度机械臂轨迹跟踪控制，基于强化学习DDPG的机械臂轨迹跟踪，控制算法，强化学习算法，将强化学习DDPG作为机械臂的轨迹跟踪控制器，simulink仿真。

在机器人领域，机械臂的轨迹跟踪控制一直是研究热点。从简单的2自由度机械臂到复杂的6自由度机械臂，如何精准控制其轨迹，关乎着各类任务的执行效果。而强化学习算法，特别是深度确定性策略梯度（DDPG），为机械臂轨迹跟踪控制带来了新的思路。

2自由度与6自由度机械臂轨迹跟踪控制基础

2自由度机械臂相对简单，通常可在平面内进行运动控制。以常见的笛卡尔坐标系下的2连杆机械臂为例，其正向运动学可通过齐次变换矩阵来描述：

import numpy as np

def forward_kinematics_2dof(theta1, theta2, l1, l2):
    T01 = np.array([[np.cos(theta1), -np.sin(theta1), 0, l1 * np.cos(theta1)],
                    [np.sin(theta1), np.cos(theta1), 0, l1 * np.sin(theta1)],
                    [0, 0, 1, 0],
                    [0, 0, 0, 1]])
    T12 = np.array([[np.cos(theta2), -np.sin(theta2), 0, l2 * np.cos(theta2)],
                    [np.sin(theta2), np.cos(theta2), 0, l2 * np.sin(theta2)],
                    [0, 0, 1, 0],
                    [0, 0, 0, 1]])
    T02 = np.dot(T01, T12)
    return T02

这段代码通过给定的关节角度 theta1、theta2 以及连杆长度 l1、l2，计算出机械臂末端在空间中的位置。对于2自由度机械臂的轨迹跟踪控制，可基于经典控制算法如PID来实现初步的位置跟踪。

然而，6自由度机械臂能在三维空间中完成更复杂的任务，其正向运动学和逆运动学的求解更为复杂。正向运动学涉及多个关节的旋转和平移变换，逆运动学则是根据目标位置和姿态求解关节角度。以常见的6R机器人（6个旋转关节）为例，其正向运动学需多次运用齐次变换矩阵的乘积来计算末端位姿。

强化学习DDPG算法

强化学习旨在通过智能体与环境的交互，让智能体学习到最优策略以最大化累积奖励。DDPG是一种基于深度神经网络的无模型强化学习算法，结合了深度Q网络（DQN）和确定性策略梯度（DPG）的思想。

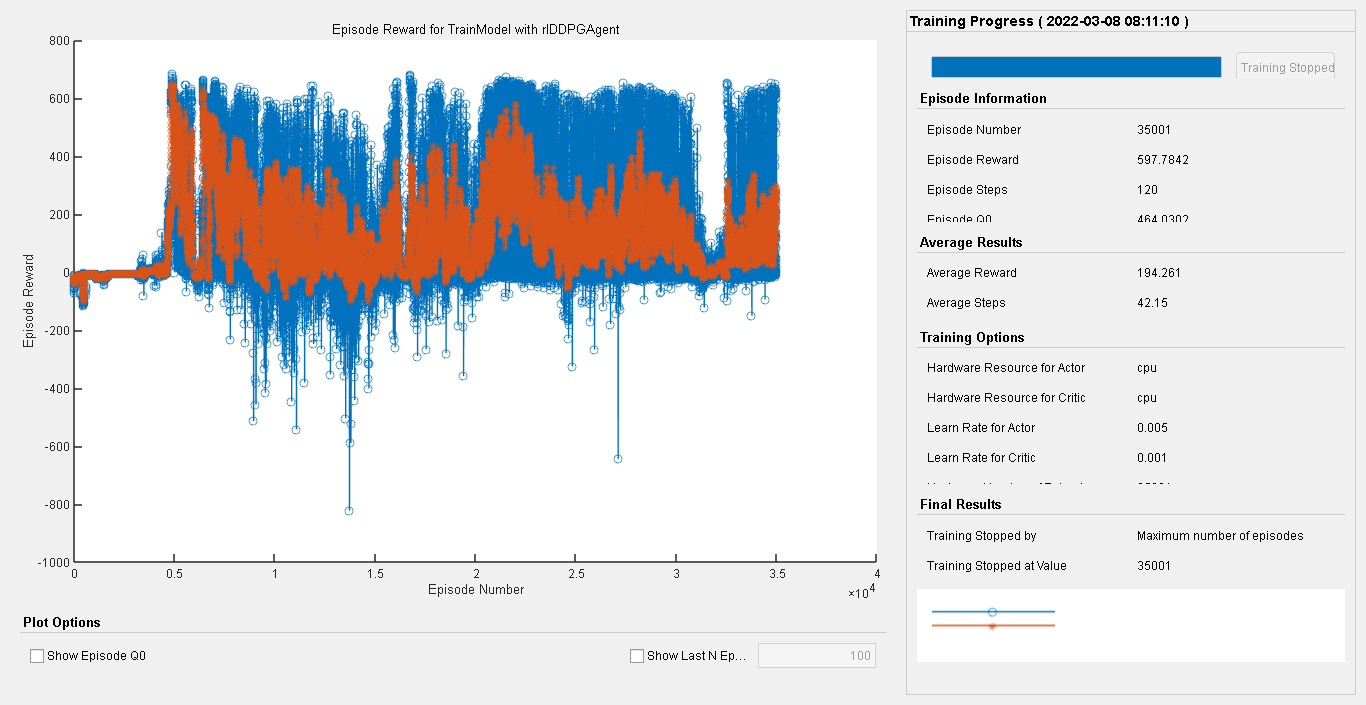
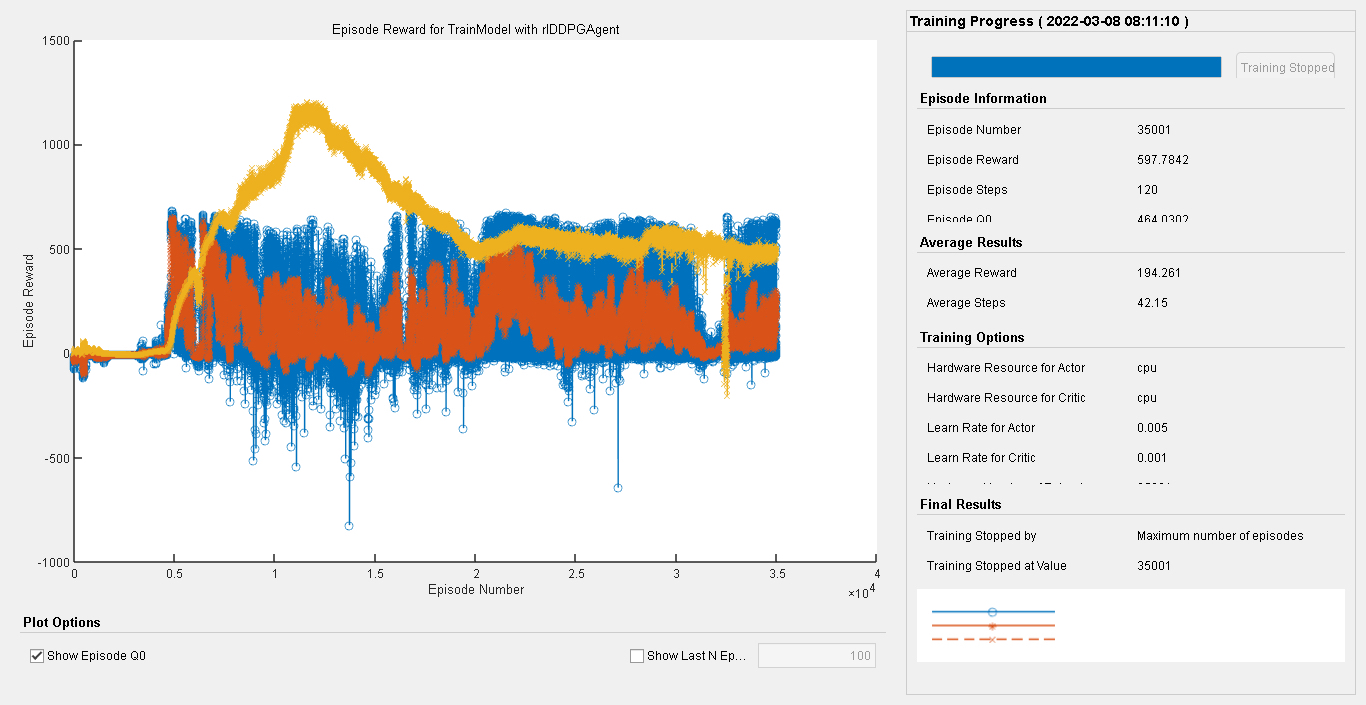
2自由度机械臂轨迹跟踪控制，6自由度机械臂轨迹跟踪控制，基于强化学习DDPG的机械臂轨迹跟踪，控制算法，强化学习算法，将强化学习DDPG作为机械臂的轨迹跟踪控制器，simulink仿真。

DDPG包含两个神经网络：策略网络（Actor）和价值网络（Critic）。策略网络输出动作，价值网络评估动作的价值。以下是一个简化的DDPG算法伪代码框架：

# 初始化Actor网络和Critic网络
actor = ActorNetwork()
critic = CriticNetwork()

# 初始化目标Actor网络和目标Critic网络
target_actor = ActorNetwork()
target_critic = CriticNetwork()

# 初始化经验回放池
replay_buffer = ReplayBuffer()

for episode in range(num_episodes):
    state = env.reset()
    for step in range(max_steps_per_episode):
        # 根据策略网络生成动作，加入噪声以增加探索
        action = actor.predict(state) + noise()
        next_state, reward, done, _ = env.step(action)
        # 将经验存储到回放池中
        replay_buffer.add(state, action, reward, next_state, done)
        state = next_state
        if done:
            break
        if len(replay_buffer) > batch_size:
            # 从回放池中采样一批经验
            batch = replay_buffer.sample(batch_size)
            states, actions, rewards, next_states, dones = batch

            # 更新Critic网络
            target_actions = target_actor.predict(next_states)
            target_q_values = target_critic.predict(next_states, target_actions)
            q_targets = rewards + (1 - dones) * gamma * target_q_values
            critic.train(states, actions, q_targets)

            # 更新Actor网络
            actor_actions = actor.predict(states)
            actor_loss = -critic.predict(states, actor_actions)
            actor.train(states, actor_loss)

            # 软更新目标网络
            target_actor.soft_update(actor)
            target_critic.soft_update(critic)

在这个框架中，智能体在环境中不断尝试不同动作，将每次交互的经验存储在回放池中。通过从回放池中采样经验数据，分别对Critic网络和Actor网络进行更新，以优化策略和评估价值。

将DDPG作为机械臂的轨迹跟踪控制器

把DDPG应用到机械臂轨迹跟踪控制中，我们可以将机械臂的状态（如关节角度、角速度等）作为状态输入给DDPG的智能体，将智能体输出的动作映射为机械臂关节的控制信号，如扭矩或速度指令。目标则是最小化机械臂末端实际位置与期望轨迹位置之间的误差，以此作为奖励信号。例如：

def get_reward(actual_position, desired_position):
    error = np.linalg.norm(actual_position - desired_position)
    # 这里简单设计奖励，误差越小奖励越大
    reward = -error
    return reward

通过不断训练，DDPG智能体可以学习到使机械臂尽可能跟踪期望轨迹的最优策略。

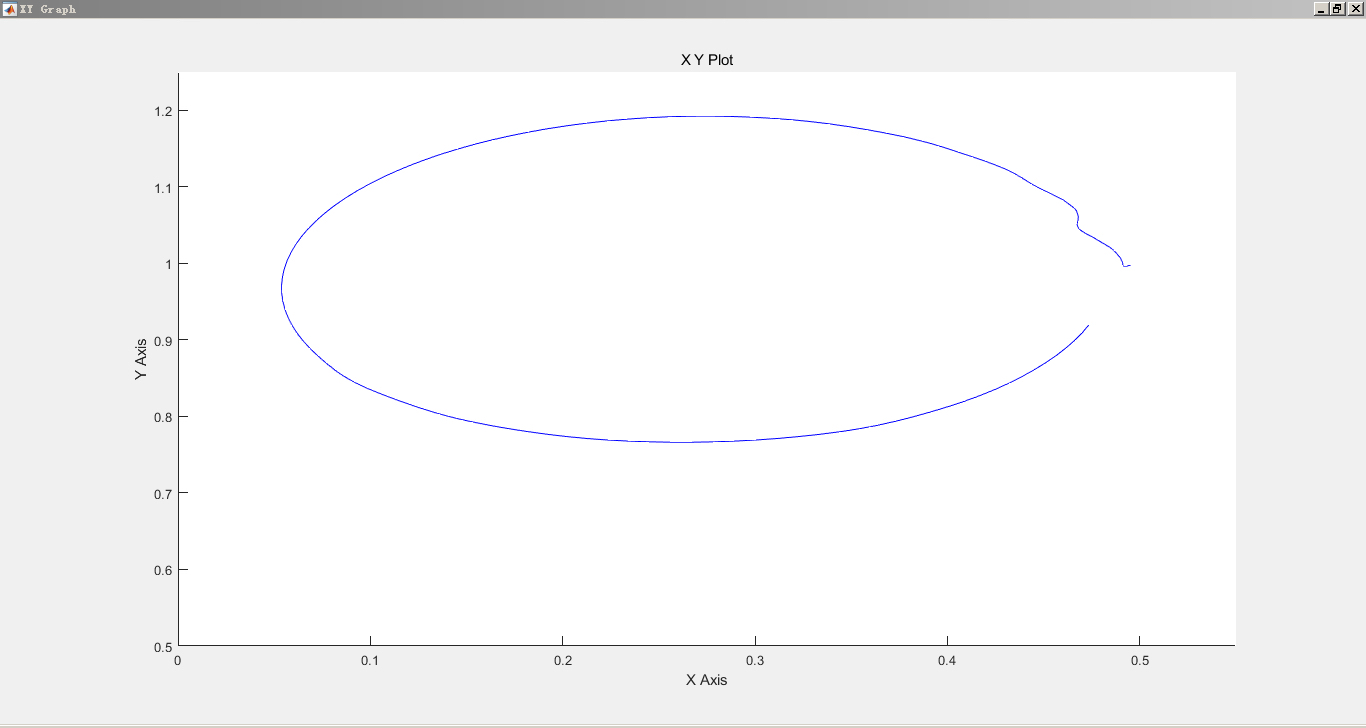
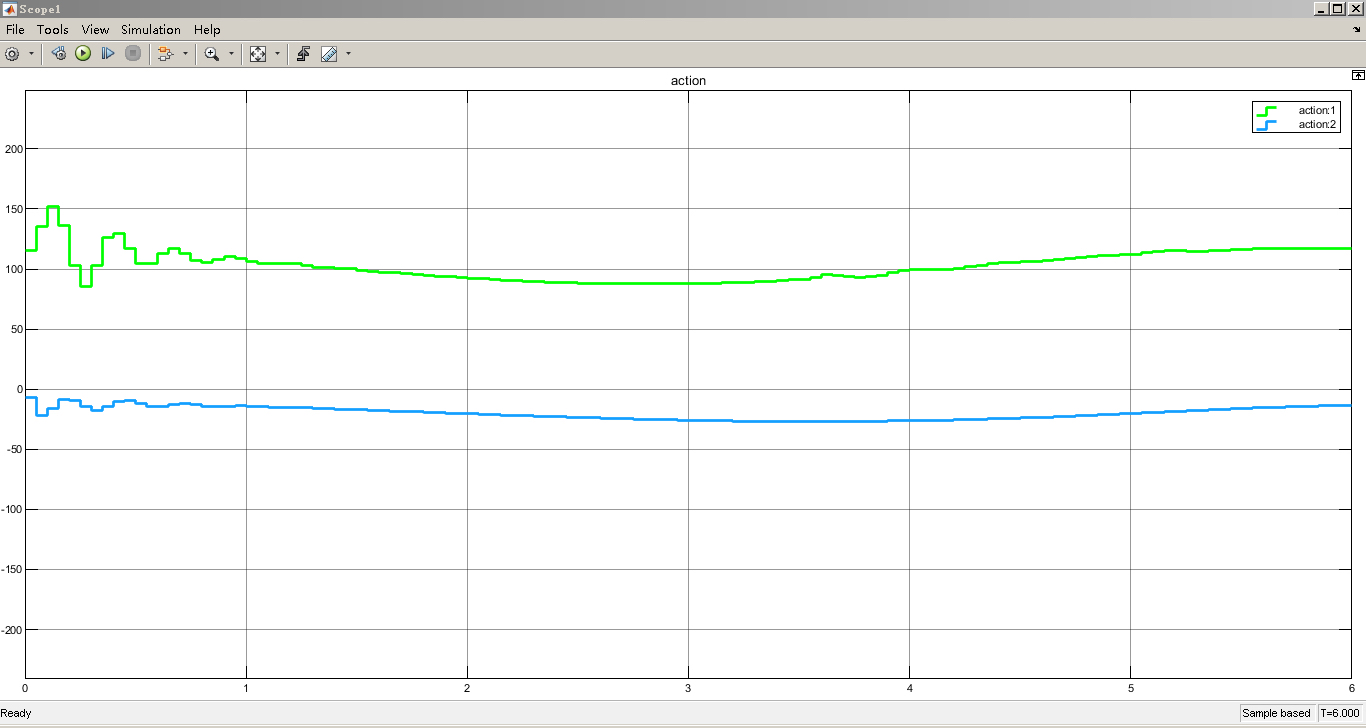
Simulink仿真

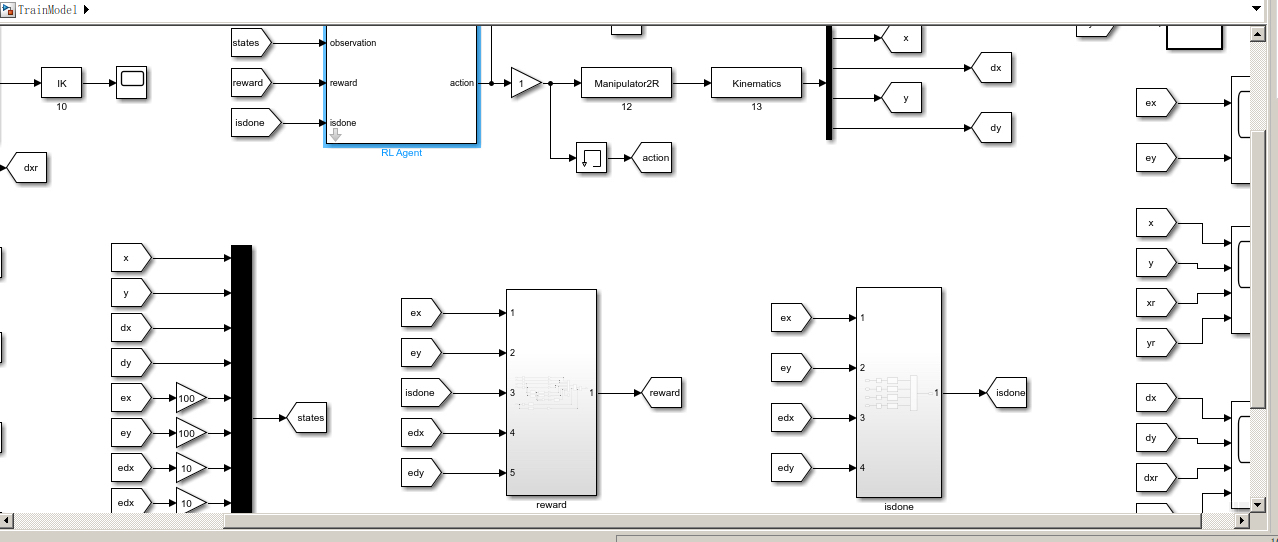
在Simulink中搭建机械臂模型进行轨迹跟踪仿真，可以直观地验证控制算法的有效性。首先，需要根据机械臂的动力学模型搭建物理模型，可使用Simscape Multibody等模块库。对于2自由度或6自由度机械臂，分别构建相应的关节和连杆结构。

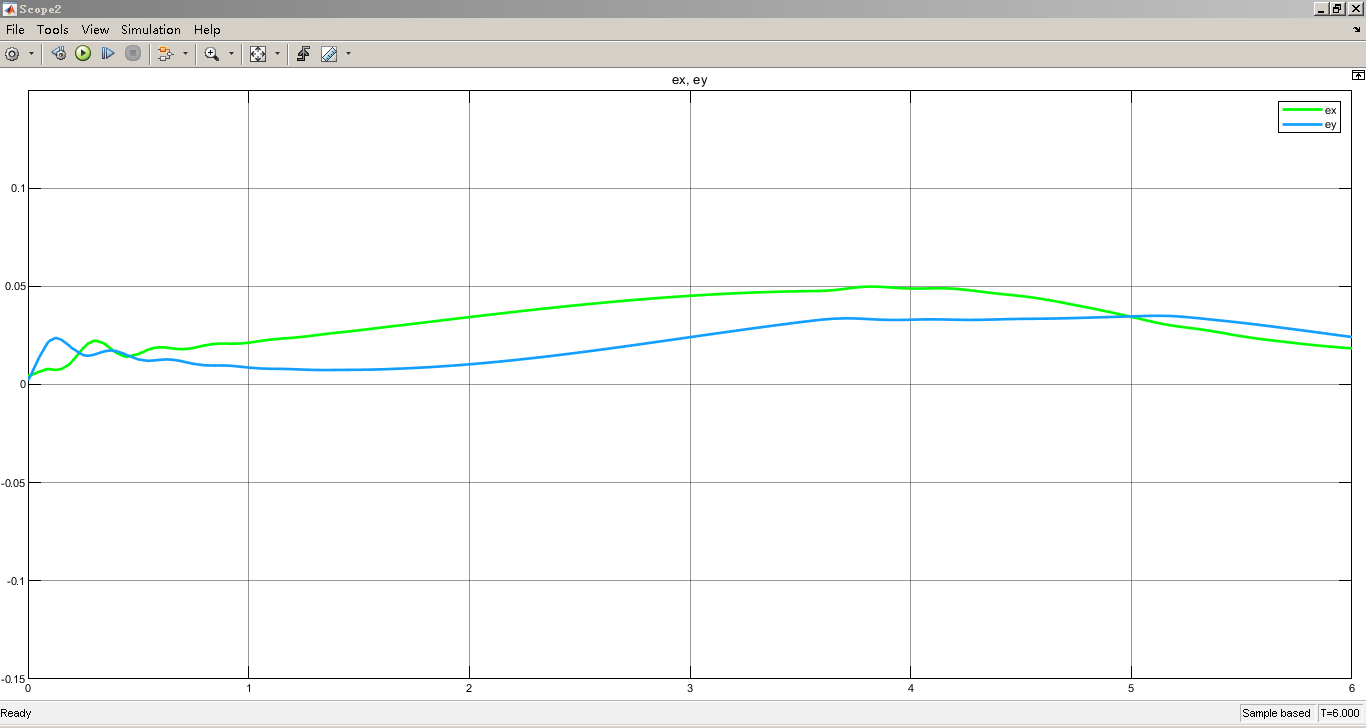
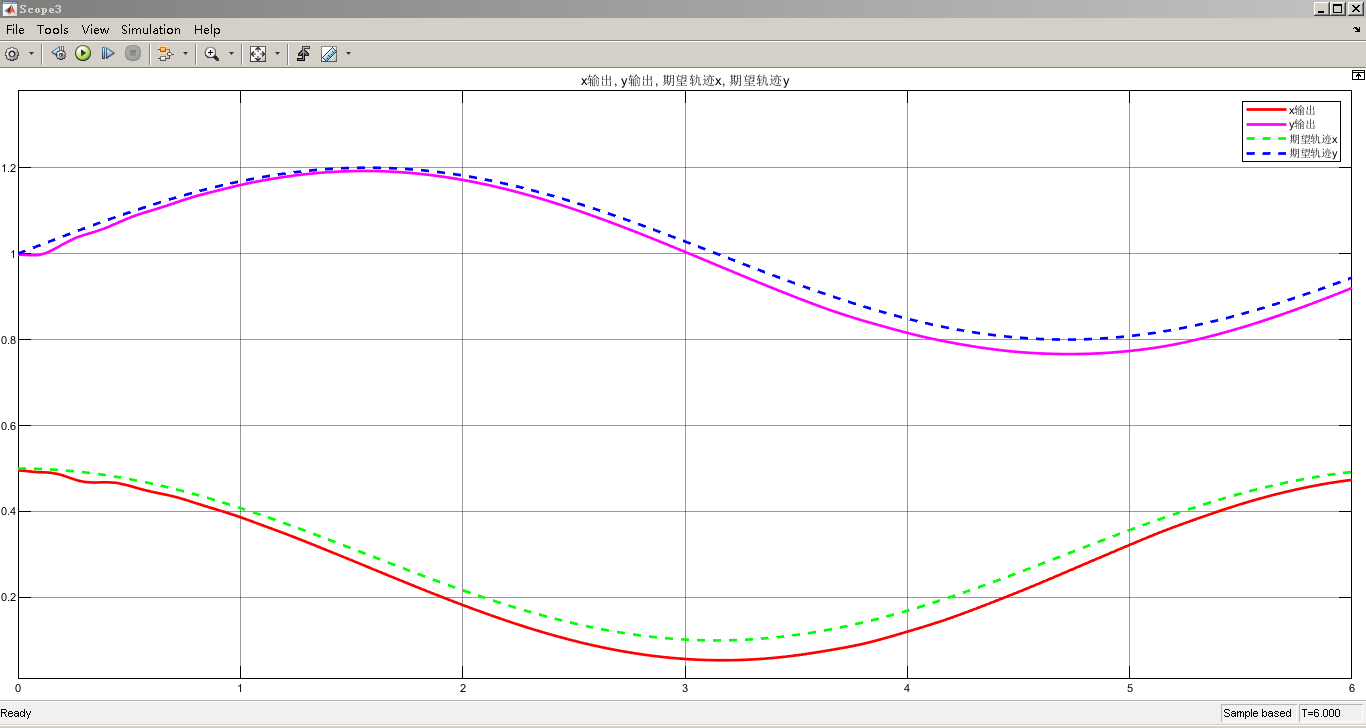
然后，将基于DDPG算法生成的控制信号输入到机械臂模型中。可以通过MATLAB Function模块编写DDPG算法代码，与Simulink模型进行交互。在仿真过程中，观察机械臂末端位置与期望轨迹的贴合程度，通过调整DDPG算法的超参数（如学习率、折扣因子等）来优化控制效果。

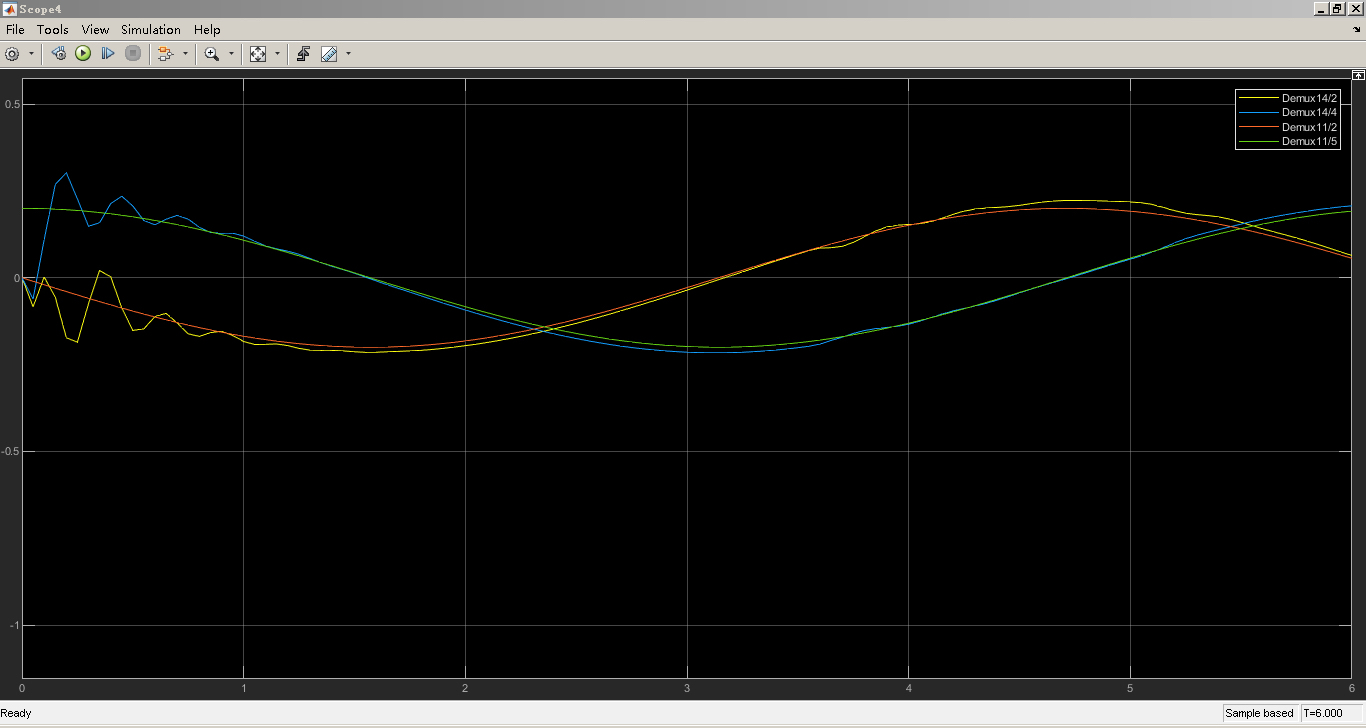
通过从2自由度到6自由度机械臂的探索，结合强化学习DDPG算法以及Simulink仿真，我们为机械臂轨迹跟踪控制提供了一套完整的研究与实践方案，不断优化算法和模型，将有助于提升机械臂在实际应用中的性能。