论文速读 Opt2Skill
Opt2Skill提出了一种结合轨迹优化与强化学习的人形机器人控制框架,通过离线生成动态可行的全身轨迹作为监督信号,训练鲁棒的RL策略。该方法利用全阶动力学优化提供精确参考轨迹,并采用非对称actor-critic架构实现从仿真到实物的迁移。实验表明,该框架能使Digit人形机器人完成爬梯、开门等复杂操作任务,在保持运动自然性的同时具备现实适应性。关键创新在于将基于模型的优化与数据驱动的学习优势相
文章目录
- Opt2Skill: Imitating Dynamically-feasible Whole-Body Trajectories for Versatile Humanoid Loco-Manipulation
- 概述
- 技术方法
- 关键实验结果
- 意义与影响
- 相关引用
-
- Deepmimic: Example-guided deep reinforcement learning of physics-based character skills
- Crocoddyl: An efficient and versatile framework for multi-contact optimal control
- Real-world humanoid locomotion with reinforcement learning
- Opt-mimic: Imitation of optimized trajectories for dynamic quadruped behaviors
Opt2Skill: Imitating Dynamically-feasible Whole-Body Trajectories for Versatile Humanoid Loco-Manipulation
- 时间:2024.9.30
- 论文:[2409.20514] Opt2Skill: Imitating Dynamically-feasible Whole-Body Trajectories for Versatile Humanoid Loco-Manipulation
概述
人形机器人在以人类为中心的环境中操作具有巨大的前景,但控制这些复杂系统以完成多功能运动操作任务仍然是一个重大挑战。传统方法面临基本限制:基于模型的优化控制方法提供精度,但面临计算复杂性和真实世界不确定性的挑战,而强化学习(RL)提供鲁棒性,但存在样本效率低下和运动不自然的问题。Opt2Skill 框架通过系统地结合这两种范式的优势来解决这些挑战,使人形机器人能够执行复杂的、接触丰富的行为。

图 1:Digit 人形机器人执行由 Opt2Skill 框架实现的多样化运动操作任务,包括爬楼梯、物体操作、开门和绘画。
技术方法
Opt2Skill 框架由三个主要组成部分构成:离线轨迹优化、基于 RL 的策略训练和直接硬件部署。
轨迹优化阶段
第一阶段使用基于全阶动力学的轨迹优化生成高质量的参考轨迹。与以往依赖简化模型或人体运动捕捉的方法不同,Opt2Skill 利用 Digit 人形机器人完整的 26-DOF 动力学(6 个未驱动的基座 DOF + 20 个驱动关节)。
优化问题表述为:
min x , u ∑ t = 0 T ∥ y t − y ^ t ∥ 2 + ∥ u t ∥ 2 \min_{x,u} \sum_{t=0}^{T} \|y_t - \hat{y}_t\|^2 + \|u_t\|^2 x,umint=0∑T∥yt−y^t∥2+∥ut∥2
受限于机器人的混合动力学、接触约束、关节限制和摩擦锥约束。其中, y t y_t yt 表示机器人的任务空间变量, y ^ t \hat{y}_t y^t 是期望的参考值, u t u_t ut 是关节扭矩。
文章使用 Crocoddyl 设定机器人运动要优化的优化函数,然后通过 DDP 求导求解出各个参数数值,进而将这些参数数值转换成机器人的动作。
求解器采用在 Crocoddyl 中实现的微分动态规划(DDP),能够高效地解决这些复杂的优化控制问题。关键的是,优化显式地包含了接触力和关节扭矩,提供动态一致的运动,尊重机器人的物理约束。
强化学习策略训练
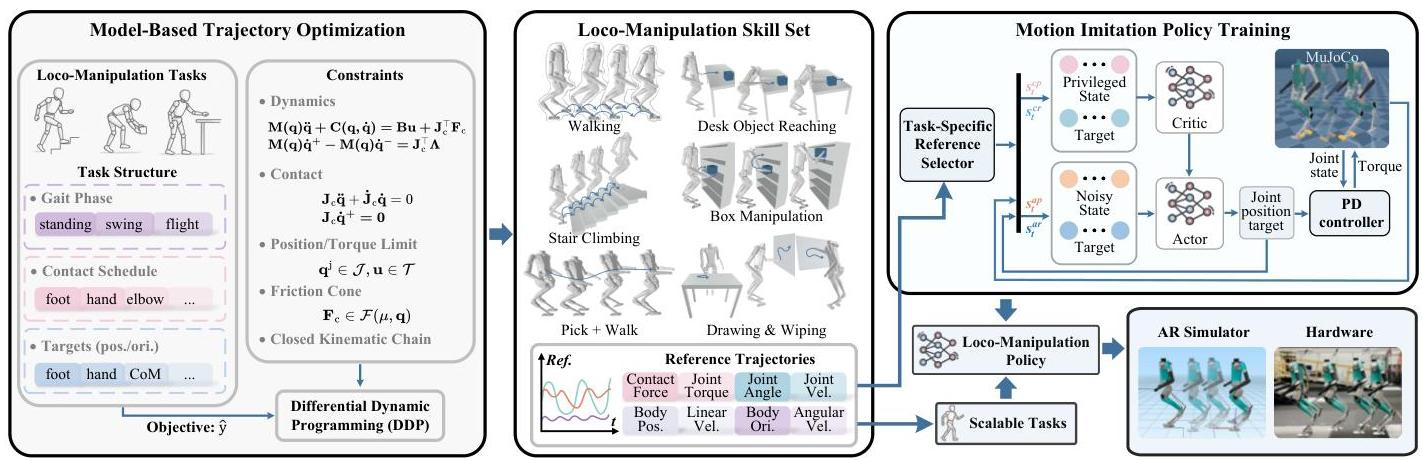
_ 图 2:Opt2Skill 框架的整体结构。 (a) 首先,我们利用轨迹优化算法生成结构化且动态上可行的参考轨迹;这些轨迹需要满足接触约束、扭矩限制以及特定任务的要求。 (b) 每条轨迹都包含了关节角度、关节速度、机体位置与方向、线速度与角速度,以及与动态行为相关的参数(如关节扭矩和相互作用力)。 © 这些参考轨迹被用作训练强化学习(RL)策略的“监督信号”;这些策略用于预测关节应达到的目标值,而这些目标值由低层的位置 - 速度(PD)控制器来实时跟踪。最终形成的强化学习策略将基于模型优化的控制策略内化为自身的行为模式,同时具备对干扰、传感器噪声以及系统动态变化的鲁棒性,从而能够直接应用于实际硬件系统中。
生成的轨迹作为监督信号,用于训练鲁棒的 RL 策略。该方法使用带有近端策略优化(PPO)的非对称 actor-critic 框架,以促进从模拟到现实的迁移:
- 评论者(Critic):可以访问特权模拟信息,包括真实状态、接触力以及完整的参考轨迹,以实现稳定的价值估计。
- 执行者(Actor):仅限于模拟真实传感器数据的噪声本体感受观测,仅接收部分参考信息(目标速度、关节位置、接触力以及扭矩)。
奖励函数结合了任务特定的跟踪目标与正则化项:
R t = R track + R torque + R force + R regularization R_t = R_{\text{track}} + R_{\text{torque}} + R_{\text{force}} + R_{\text{regularization}} Rt=Rtrack+Rtorque+Rforce+Rregularization
重要的是,该框架包括专门用于关节扭矩跟踪和接触力跟踪的奖励,利用了全阶轨迹优化中可用的独特动态信息。
在部署阶段,策略会使用根据具体测试场景新生成的离线轨迹数据作为参考;此时不会重新使用训练数据,也不会再次运行轨迹规划算法。
RL 详细设置
Tab1 :奖励设置
| 类别 | 术语;专业名词 | 表达式 | 重量 |
|---|---|---|---|
| 任务奖励 | 关节位置 | exp ( − 5 ∣ q ^ t j − q t j ∣ 2 2 ) \exp(-5|\hat{\mathbf{q}}_t^{\mathrm{j}} - \mathbf{q}_t^{\mathrm{j}}|_2^2) exp(−5∣q^tj−qtj∣22) | 0.30 |
| 基座位置 | exp ( − 20 ∣ p ^ t b − p t b ∣ 2 2 ) \exp(-20|\hat{\mathbf{p}}_t^{\mathrm{b}} - \mathbf{p}_t^{\mathrm{b}}|_2^2) exp(−20∣p^tb−ptb∣22) | 0.30 | |
| 基座方向 | exp ( − 50 ∣ θ ^ t b − θ t b ∣ 2 2 ) \exp(-50|\hat{\boldsymbol{\theta}}_t^{\mathrm{b}} - \boldsymbol{\theta}_t^{\mathrm{b}}|_2^2) exp(−50∣θ^tb−θtb∣22) | 0.30 | |
| 基座线速度 | exp ( − 2 ∣ p ˙ ^ t b − p ˙ t b ∣ 2 2 ) \exp(-2|\hat{\dot{\mathbf{p}}}_t^{\mathrm{b}} - \dot{\mathbf{p}}_t^{\mathrm{b}}|_2^2) exp(−2∣p˙^tb−p˙tb∣22) | 0.30 | |
| 基座角速度 | exp ( − 0.5 ∣ ω ^ t b − ω t b ∣ 2 2 ) \exp(-0.5|\hat{\boldsymbol{\omega}}_t^{\mathrm{b}} - \boldsymbol{\omega}_t^{\mathrm{b}}|_2^2) exp(−0.5∣ω^tb−ωtb∣22) | 0.30 | |
| 末端执行器的位置 | exp ( − 20 ∣ p ^ t e − p t e ∣ 2 2 ) \exp(-20|\hat{\mathbf{p}}_t^{\mathrm{e}} - \mathbf{p}_t^{\mathrm{e}}|_2^2) exp(−20∣p^te−pte∣22) | 0.30 | |
| 关节扭矩 | exp ( − 0.01 ∣ u ^ t − u t ∣ 2 2 ) \exp(-0.01|\hat{\mathbf{u}}_t - \mathbf{u}_t|_2^2) exp(−0.01∣u^t−ut∣22) | 0.10 | |
| 接触力 | exp ( − 0.05 ∣ F ^ t c − F t c ∣ 1 ) \exp(-0.05|\hat{\mathbf{F}}_t^{\mathrm{c}} - \mathbf{F}_t^{\mathrm{c}}|_1) exp(−0.05∣F^tc−Ftc∣1) | 0.10 | |
| 惩罚 | 动作频率(即用户每单位时间执行操作的次数) | ∣ a t − 2 a t − 1 + a t − 2 ∣ 2 2 |\mathbf{a}_t - 2\mathbf{a}_{t-1} + \mathbf{a}_{t-2}|_2^2 ∣at−2at−1+at−2∣22 | -0.05 |
| 扭矩 | ∣ u t / u l i m i t ∣ 2 2 |\mathbf{u}_t / \mathbf{u}_{\mathrm{limit}}|_2^2 ∣ut/ulimit∣22 | -0.03 | |
| 关节加速度 | ∣ d o t q t j ∣ 2 2 |dot{\mathbf{q}}_t^{\mathrm{j}}|_2^2 ∣dotqtj∣22 | − 10 − 6 -10^{-6} −10−6 |
请注意:“基座位置”奖励并不包含在“步行”任务中。
Tab2:域随机化
| 类别 | 参数 | 类型 | 范围 / 标准差 |
|---|---|---|---|
| 观测 | 关节位置 | 加性(高斯) | σ = 0.0875 \sigma = 0.0875 σ=0.0875 |
| 关节速度 | 加性(高斯) | σ = 0.075 \sigma = 0.075 σ=0.075 | |
| 基座线速度 | 加性(高斯) | σ = 0.15 \sigma = 0.15 σ=0.15 | |
| 基座角速度 | 加性(高斯) | σ = 0.15 \sigma = 0.15 σ=0.15 | |
| 重力投影 | 加性(高斯) | σ = 0.075 \sigma = 0.075 σ=0.075 | |
| 延迟 | 动作延迟 | 均匀 | [ 0.0 , 0.02 ] s [0.0, 0.02]\,\text{s} [0.0,0.02]s |
| 电机 | 电机强度 | 缩放(均匀) | [ 0.95 , 1.05 ] [0.95, 1.05] [0.95,1.05] |
| Kp/Kd 系数 | 缩放(均匀) | [ 0.9 , 1.1 ] [0.9, 1.1] [0.9,1.1] | |
| 身体 | 质量 | 缩放(均匀) | [ 0.9 , 1.1 ] [0.9, 1.1] [0.9,1.1] |
| 环境 | 重力 | 缩放(均匀) | [ 0.9 , 1.1 ] [0.9, 1.1] [0.9,1.1] |
| 摩擦 | 缩放(均匀) | [ 0.3 , 1.0 ] [0.3, 1.0] [0.3,1.0] | |
| 地形 | 离散 | flat, rough 平坦、崎岖 |
观测空间
critic:
评论器的观测空间定义为 o critic = [ s t c p ; s t c r ] \mathbf{o}_{\text{critic}} = \left[ \mathbf{s}_t^{cp};\ \mathbf{s}_t^{cr} \right] ocritic=[stcp; stcr] ,其中特权本体感知 s t c p \mathbf{s}_t^{cp} stcp 为 [ p t b , θ t b , p ˙ t b , ω t b , g t , q t j , h i s t , q ˙ t j , p t e , a h i s t , F t c , u t , K p , K d ] [\mathbf{p}_t^b,\ \boldsymbol{\theta}_t^b,\ \dot{\mathbf{p}}_t^b,\ \boldsymbol{\omega}_t^b,\ \mathbf{g}_t,\ \mathbf{q}_t^{\mathrm{j,hist}},\ \dot{\mathbf{q}}_t^{\mathrm{j}},\ \mathbf{p}_t^e,\ \mathbf{a}_{\mathrm{hist}},\ \mathbf{F}_t^c,\ \mathbf{u}_t,\ \mathbf{K}_p,\ \mathbf{K}_d] [ptb, θtb, p˙tb, ωtb, gt, qtj,hist, q˙tj, pte, ahist, Ftc, ut, Kp, Kd] ,包括人形机器人身体平移 p t b \mathbf{p}_t^b ptb 、姿态 θ t b \boldsymbol{\theta}_t^b θtb 、线速度 p ˙ t b \dot{\mathbf{p}}_t^b p˙tb 、角速度 ω t b \boldsymbol{\omega}_t^b ωtb 、投影重力 g t \mathbf{g}_t gt (作为基座姿态的代理)、以每 δ = 4 \delta = 4 δ=4 个时间步采样一次的 N = 10 N = 10 N=10 个历史电机关节位置 q t j , h i s t = [ q t j , q t − δ j , … , q t − ( N − 1 ) δ j ] \mathbf{q}_t^{\mathrm{j,hist}} = [\mathbf{q}_t^{\mathrm{j}}, \mathbf{q}_{t-\delta}^{\mathrm{j}}, \dots, \mathbf{q}_{t-(N-1)\delta}^{\mathrm{j}}] qtj,hist=[qtj,qt−δj,…,qt−(N−1)δj] (即 50 Hz 采样自 200 Hz 控制回路)、电机关节速度 q ˙ t j \dot{\mathbf{q}}_t^{\mathrm{j}} q˙tj 、末端执行器位置(相对于躯干) p t e \mathbf{p}_t^e pte 、以相同频率采样的 N N N 个历史动作 a h i s t = [ a t − 1 , a t − ( 1 + δ ) , … , a t − ( 1 + ( N − 1 ) δ ) ] \mathbf{a}_{\mathrm{hist}} = [\mathbf{a}_{t-1}, \mathbf{a}_{t-(1+\delta)}, \dots, \mathbf{a}_{t-(1+(N-1)\delta)}] ahist=[at−1,at−(1+δ),…,at−(1+(N−1)δ)] 、接触力 F t c \mathbf{F}_t^c Ftc 、关节力矩 u t \mathbf{u}_t ut 以及 PD 增益 K p \mathbf{K}_p Kp 、 K d \mathbf{K}_d Kd 。参考状态 s t c r \mathbf{s}_t^{cr} stcr 定义为 [ p ^ t b , θ ^ t b , p ˙ ^ t b , ω ^ t b , q ^ t j , q ˙ ^ t j , p ^ t e , F ^ t c , u ^ t ] [\hat{\mathbf{p}}_t^b,\ \hat{\boldsymbol{\theta}}_t^b,\ \hat{\dot{\mathbf{p}}}_t^b,\ \hat{\boldsymbol{\omega}}_t^b,\ \hat{\mathbf{q}}_t^{\mathrm{j}},\ \hat{\dot{\mathbf{q}}}_t^{\mathrm{j}},\ \hat{\mathbf{p}}_t^e,\ \hat{\mathbf{F}}_t^c,\ \hat{\mathbf{u}}_t] [p^tb, θ^tb, p˙^tb, ω^tb, q^tj, q˙^tj, p^te, F^tc, u^t] ,其中帽子 ( ^ \hat{} ^ ) 表示参考轨迹信息。
actor:
执行器的观测空间定义为 o actor = [ s t a p ; s t a r ] \mathbf{o}_{\text{actor}} = \left[ \mathbf{s}_t^{ap};\ \mathbf{s}_t^{ar} \right] oactor=[stap; star] ,其中噪声本体感知 s t a p \mathbf{s}_t^{ap} stap 为 [ p ~ t b , ω ~ t b , g ~ t , q ~ t j , h i s t , q ˙ ~ t j , a h i s t ] [\tilde{\mathbf{p}}_t^b,\ \tilde{\boldsymbol{\omega}}_t^b,\ \tilde{\mathbf{g}}_t,\ \tilde{\mathbf{q}}_t^{\mathrm{j,hist}},\ \tilde{\dot{\mathbf{q}}}_t^{\mathrm{j}},\ \mathbf{a}_{\mathrm{hist}}] [p~tb, ω~tb, g~t, q~tj,hist, q˙~tj, ahist] ,波浪号 ( ~ \tilde{} ~ ) 表示带噪传感器测量。执行器还接收部分参考信息 s t a r = [ p ^ t b , ω ^ t b , q ^ t j , F ^ t c , u ^ t ] \mathbf{s}_t^{ar} = [\hat{\mathbf{p}}_t^b,\ \hat{\boldsymbol{\omega}}_t^b,\ \hat{\mathbf{q}}_t^{\mathrm{j}},\ \hat{\mathbf{F}}_t^c,\ \hat{\mathbf{u}}_t] star=[p^tb, ω^tb, q^tj, F^tc, u^t] 。执行器仅接收部分参考,以确保泛化并避免依赖噪声或冗余输入(如全局基座状态或末端执行器姿态),而评论器则可访问完整的特权信息以实现稳定的价值估计。
控 制 策 略 的 动 作 空 间 表 示 相 对 于 默 认 站 立 姿 态 的 偏 移 量,用 于 指 定 20 个 驱 动 关 节 的 目 标 位 置。这 些 目 标 被 输 入 到 一 个 PD 关 节 扭 矩 控 制 器,其 扭 矩 计 算 为 u t = K p ( a t + q d f l t j − q t j ) − K d q ˙ t j \mathbf{u}_t = \mathbf{K}_p(\mathbf{a}_t + \mathbf{q}_{\mathrm{dflt}}^{\mathrm{j}} - \mathbf{q}_t^{\mathrm{j}}) - \mathbf{K}_d\dot{\mathbf{q}}_t^{\mathrm{j}} ut=Kp(at+qdfltj−qtj)−Kdq˙tj。其 中, q d f l t j \mathbf{q}_{\mathrm{dflt}}^{\mathrm{j}} qdfltj 表 示 默 认 站 立 时 的 关 节 位 置, q t j \mathbf{q}_t^{\mathrm{j}} qtj 和 q ˙ t j \dot{\mathbf{q}}_t^{\mathrm{j}} q˙tj 分 别 为 测 得 的 关 节 位 置 和 速 度。我 们 的 控 制 策 略 以 200 Hz 运 行,而 内 部 PD 控 制 器 在 仿 真(训 练 阶 段)中 以 1 kHz 运 行,在 硬 件(部 署 阶 段)中 以 2 kHz 运 行。策 略 输 出 与 PD 控 制 回 路 之 间 未 施 加 显 式 滤 波。在 硬 件 上,我 们 使 用 与 仿 真 相 同 的 PD 增 益,并 直 接 将 扭 矩 指 令 发 送 给 机 器 人。
关键实验结果
与替代参考数据的比较
作者将 Opt2Skill 与使用人体运动捕捉数据和基于逆运动学(IK)参考的基线进行了比较。在多项指标上,Opt2Skill 表现出卓越的性能:
- 手部跟踪误差:2.00 厘米 (Opt2Skill) vs 4.25 厘米 (Human) vs 5.47 厘米 (IK)
- 基础位置漂移:1.14% (Opt2Skill) vs 替代方案显著更高
- 全局稳定性:更低的侧向漂移 (0.06 毫米/帧) 和偏航漂移 (0.02 毫弧度/帧)
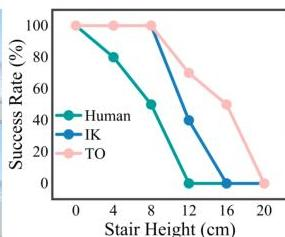
图 3:在挑战性地形上的成功率,显示了 Opt2Skill 在楼梯(左)和斜坡(右)上比人类动作捕捉和基于 IK 的参考方案具有更优异的鲁棒性。
动态信息的重要性
一项关于接触密集擦拭任务的消融研究揭示了关节力矩信息的关键作用。使用位置和力矩参考(Pos+T)训练的策略显著优于仅使用位置(Pos)的策略,而同时结合力矩和力参考(Pos+F+T)则实现了最佳的接触力跟踪性能。
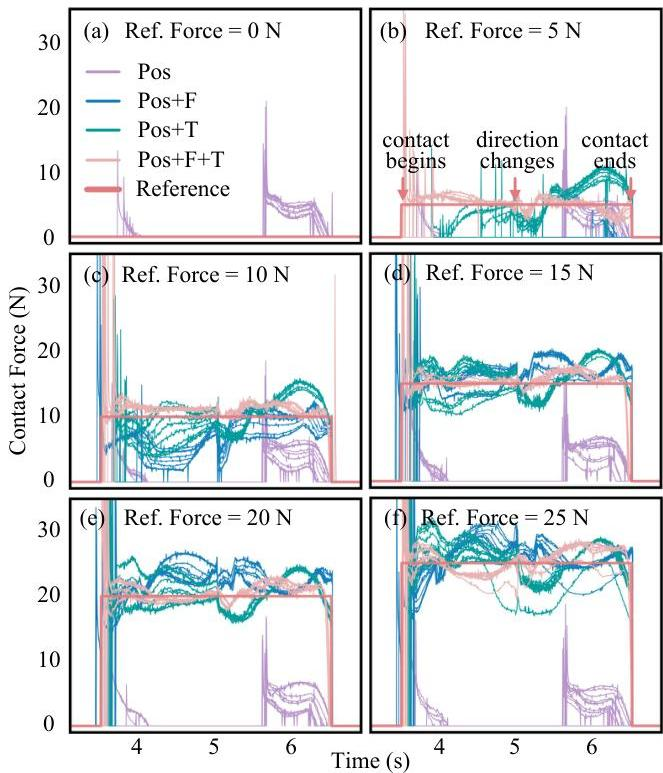
图 4:不同参考力水平下的接触力跟踪,表明结合力矩信息(Pos+T,Pos+F+T)可以实现更准确和一致的力施加。
硬件验证
该框架成功转移到真实的 Digit 机器人上,无需任何在线适应或硬件特定调整。演示的能力包括:
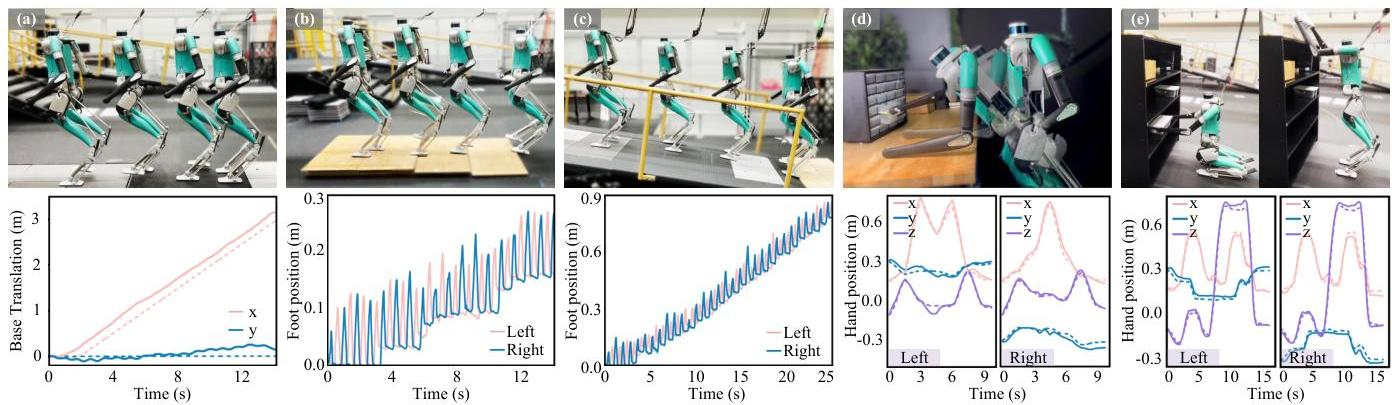
图 5:硬件实验显示 (a) 平地行走,基座跟踪准确;(b) 爬楼梯;© 斜坡穿越;(d) 桌面物体抓取,具有多接触稳定性;以及 (e) 盒子操作任务。
- 运动能力:准确的平地行走,成功爬上高达 12 厘米的楼梯,以及穿越高达 19.5° 的斜坡
- 多接触操作:桌面物体抓取,平均手部跟踪误差为 3.7-3.8 厘米,盒子拾取和放置的平均误差为 3.6 厘米
- 复杂行为:举起重箱 (4.9 公斤),拾取 - 行走序列,开门,以及同时绘画和擦拭

图 6:扩展的硬件演示,包括拾取 - 行走序列、开门、重箱操作以及双臂绘画和擦拭任务。
意义与影响
Opt2Skill 通过有效连接基于模型的优化和强化学习,代表了类人机器人控制领域的重大进展。其主要贡献包括:
方法论创新:该框架提供了一种生成高保真参考数据的原则性方法,消除了人类动作捕捉中存在的具身化差距,同时全程保持了动态可行性。
动态一致性:通过整合全阶动力学、关节力矩和接触力,该方法生成了物理上基础牢固的参考运动,从而实现更准确的跟踪和更稳健的接触交互。
多功能能力:所展示的运动 - 操作技能范围——从精确的运动到复杂的物体操作——展示了该框架在实现真正多功能类人机器人行为方面的潜力。
实际部署:在没有大量硬件调优的情况下成功实现了模拟到现实的迁移,证明了该方法在实际应用中的可行性。
Opt2Skill 框架为类人机器人在需要与人类环境进行复杂物理交互的应用中开辟了新的可能性,从物流和辅助机器人到灾难响应场景。通过提供一种可扩展的方法来生成多样化、动态可行的技能,它推动了该领域向更强大、更稳健的类人机器人系统发展。
相关引用
Deepmimic: Example-guided deep reinforcement learning of physics-based character skills
本文为 Opt2Skill 的强化学习方面奠定了基础。它引入了“DeepMimic”框架,用于通过模仿参考动作来学习技能,这是 Opt2Skill 训练其人形控制策略并设计其奖励函数所采纳的核心原则。
X. B. Peng, P. Abbeel, S. Levine, and M. Van de Panne, “Deepmimic: Example-guided deep reinforcement learning of physics-based character skills,” ACM Transactions On Graphics, vol. 37, no. 4, pp. 1–14, 2018.
Crocoddyl: An efficient and versatile framework for multi-contact optimal control
这篇引用至关重要,因为它提供了 Opt2Skill 流程中 ‘Opt’ 阶段所使用的特定轨迹优化框架 Crocoddyl。主论文依赖于这个基于 DDP 的求解器来生成高质量、动态可行的参考轨迹,这些轨迹是其方法论的核心。
C. Mastalli, R. Budhiraja, W. Merkt, G. Saurel, B. Hammoud, M. Naveau, J. Carpentier, L. Righetti, S. Vijayakumar, and N. Mansard, “Crocoddyl: An efficient and versatile framework for multi-contact optimal control,” in IEEE International Conference on Robotics and Automation, 2020, pp. 2536–2542.
Real-world humanoid locomotion with reinforcement learning
本文在人形机器人平台 Digit 上的模拟到真实 (sim-to-real) 强化学习方面确立了最先进水平。它是至关重要的参考,且 Opt2Skill 论文借鉴了其 sim-to-real 技术,例如域随机化,使其对于验证硬件部署具有高度相关性。
I. Radosavovic, T. Xiao, B. Zhang, T. Darrell, J. Malik, and K. Sreenath, “Real-world humanoid locomotion with reinforcement learning,” Science Robotics, vol. 9, no. 89, p. eadi9579, 2024.
Opt-mimic: Imitation of optimized trajectories for dynamic quadruped behaviors
作者认为这是一项“密切相关的研究”,该研究同样结合了轨迹优化、模仿学习和扭矩监督。将其纳入讨论很重要,因为它突出了 Opt2Skill 的具体贡献,例如将这一概念应用于使用全阶动力学模型的高自由度双足人形机器人,而非四足机器人。
Y. Fuchioka, Z. Xie, and M. Van de Panne, “Opt-mimic: Imitation of optimized trajectories for dynamic quadruped behaviors,” in International Conference on Robotics and Automation, 2023, pp. 5092–5098.

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)