运动控制先导课（一）——微分方程与拉普拉斯变换

运动控制先导课（一）——搓机器人就要涉及运动控制系统，描述控制系统就要用微分方程，那么微分方程如何建立？为什么要用拉氏变换解微分方程，又如何进行拉氏变换？

2301_80226956

1300人浏览 · 2025-05-14 08:30:00

2301_80226956 · 2025-05-14 08:30:00 发布

引言

设计或选择机器人运动控制系统时，不可避免地要对这个系统进行分析，看看这个系统响应快不快，精度如何？可调范围大不大？输入输出关系如何？等等。此外我们还希望知道多个子系统耦合的复杂系统是否也满足这些要求。
因此，这门课程将从单个环节分析走向多个系统的复杂分析，通过动态结构图和传递函数描述和分析系统。

这往往需要一些不那么简单的手段比如拉氏变换、梅森公式、bode图等工具，以及一些前导理论，本课程希望低开高走，看完直接可以进入运动控制系统的学习。

这门课是机器人运动控制学的先导课，尽可能完课后再学机器人运动控制学，这门课将在同一文件夹下可以找到，欢迎食用。（已构建完成，正在润色）

主食来源：BILIBILI @小葵花自控课堂 @俗人Carp
本课程是两位大佬课程的对应笔记以及个人理解。

这门课可以放心追，已经码完字了，基本是排排版就可以发。

系统分析

这个部分只是希望能给你留个印象，知道接下来系统分析会如何展开，一旦哪一步不知道为什么要这么干了，就可以回来看一看为什么这么做。

不用担心，在最后我们收束的时候还会再次更细地捋一次思路。

分析系统的核心就是研究其输入输出关系。

这种关系可以通过以下几种形式描述：

微分方程：直接描述系统的动态行为。
传递函数：在频域中描述输入和输出的关系。
时域响应：输入信号（如阶跃信号）下系统的输出信号y(t)。一般用阶跃响应图呈现。

快速入门：

我们的目的是研究系统的输入与输出关系，而一个系统的输入输出关系可以用微分方程表示。

这是一个微分方程：

$\frac{d^2 y(t)}{dt^2} + 3 \frac{dy(t)}{dt} + 2 y(t) = u(t)$

微分方程由于具有高阶导，很难求解，但理解很直观。

拉普拉斯变换是一种可逆函数，可以简化微分方程为普通代数方程。

这是由上面微分方程拉氏变换的代数方程：

$G(s) = \frac{Y(s)}{U(s)} = \frac{1}{s^2 + 3s + 2}$

拉氏变换后的代数方程方便计算，但抽象，不直观。

微分方程在拉普拉斯变换后计算完，可以进行反拉氏变换得到在微分形式下的解。

零初始条件是指系统启动t=0时的状态，

在零初始条件下，这个代数方程可以化简为一种便于分析的传递函数。

为了直观展示输入输出的关系，我们采用阶跃响应图直观展示输出与时间的关系。

一个系统由若干典型环节构成，描绘和分析复杂的系统需要动态结构图。

动态结构图可以由典型环节通过串联、并联、反馈耦合构成，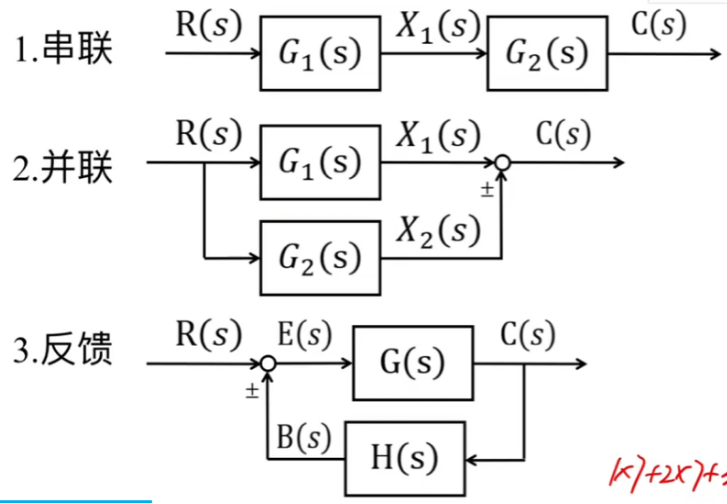

通过动态结构图可以得到传递函数，通过梅森公式也可以得到传递函数。

由此就可以进入开环系统和闭环系统的学习。

以上就是本课程的逻辑。

因此，为了直观展示输入输出关系，并分析系统特性，

①我们首先要写出系统的微分方程，直观描绘输入输出关系，但由于难求解，

②因此需要在零初始条件下进行拉普拉斯变换，得到传递函数，求解。

③传递函数由于比较抽象，且不含时间参数，无法绘图（响应图的参数含时间t），

④因此反拉氏变换得到解y(t)的显式表达式，

⑤最后绘出阶跃响应图。

对应接下来几节我们会回应：

有哪些常见系统？如何判断系统类型？

（一）如何研究一个系统：

数学模型的建立

如何写系统的微分方程？

（一）拉普拉斯变换是什么？性质？定理？

如何用拉普拉斯变换求解微分方程？

零初始条件是什么？

反拉普拉斯变换？

（二）拉普拉斯变换与传递函数

传递函数如何得到的？

传递函数的性质？

（三）传递函数的零点极点与模态？

（四）典型环节系统的传递函数及性质

从环节到系统

（五）动态结构图为何建立？如何建立？

（六）如何化简一个动态结构图？

如何通过动态结构图得到传递函数？

（七）如何用梅森公式得到传递函数？

（八）基本的开环与闭环函数

这个up更到哪这就同步到哪，兴许还会补充？

控制系统的分类：

根据是否可以通过线性微分方程描述可以分为线性系统非线性系统。

根据系统的参数是否随时间变化可以分为定常（时不变）系统时变系统，也就是说，系统的响应是否仅取决于输入和系统的初态。

我们这门课主要研究线性时不变系统。

线性系统：

由线性微分方程、差分方程描述的系统。

线性系统自然和线性代数一样，满足叠加性齐次性（倍数关系）。

判断系统是否满足线性：

定理：微分积分由于可叠加性和齐次性，因此在方程中并不影响线性性

若方程
含微分（高阶微分）、积分、原函数，一般是线性系统，
但凡含常数项、原函数高次项，都是非线性系统。
例如：
$u(x) = {5 + r^2(x)} + t \frac{d^2 r(t)}{dt^2}$ —— 非线性时变系统（包含常数了）
$\frac{d^3 u(t)}{dt^3} + 3 \frac{d^2 u(t)}{dt^2} + 6 \frac{du(t)}{dt} = r(t)$ —— 线性时不变系统

注意：高阶导仍是线性的！

（以上依照是否能满足线性系统的“叠加性”和“齐次性”即可证明。）

定常（时不变）系统：

微分方程的系数不是时间的函数，则称为定常系统，此时系统的响应仅取决于输入和系统的初态。

还有一种较为特殊的系统，

线性延迟系统，在某一时刻前输出为0，此后为线性，相当于输出延迟了一段时间才跟上。

了解完常见的系统类型后我们开始尝试描述这个系统，

控制系统的数学模型：

数学模型就是对现实系统或过程的抽象描述，比如方程 F=ma 。

建立数学模型的方法：

我们通常使用微分方程来建立数学模型（方程），有两种方式：

Ⅰ 分析法：依托物理定律建立。

Ⅱ 系统辨识法（实验法）：由规律得到的。

微分方程的构建

步骤：

① 明确输入输出。

② 根据物理定律或实验规律建立微分方程组。

③ 消去中间变量，化成标准形式：输出在左，输入在右，降幂排列。

比如，

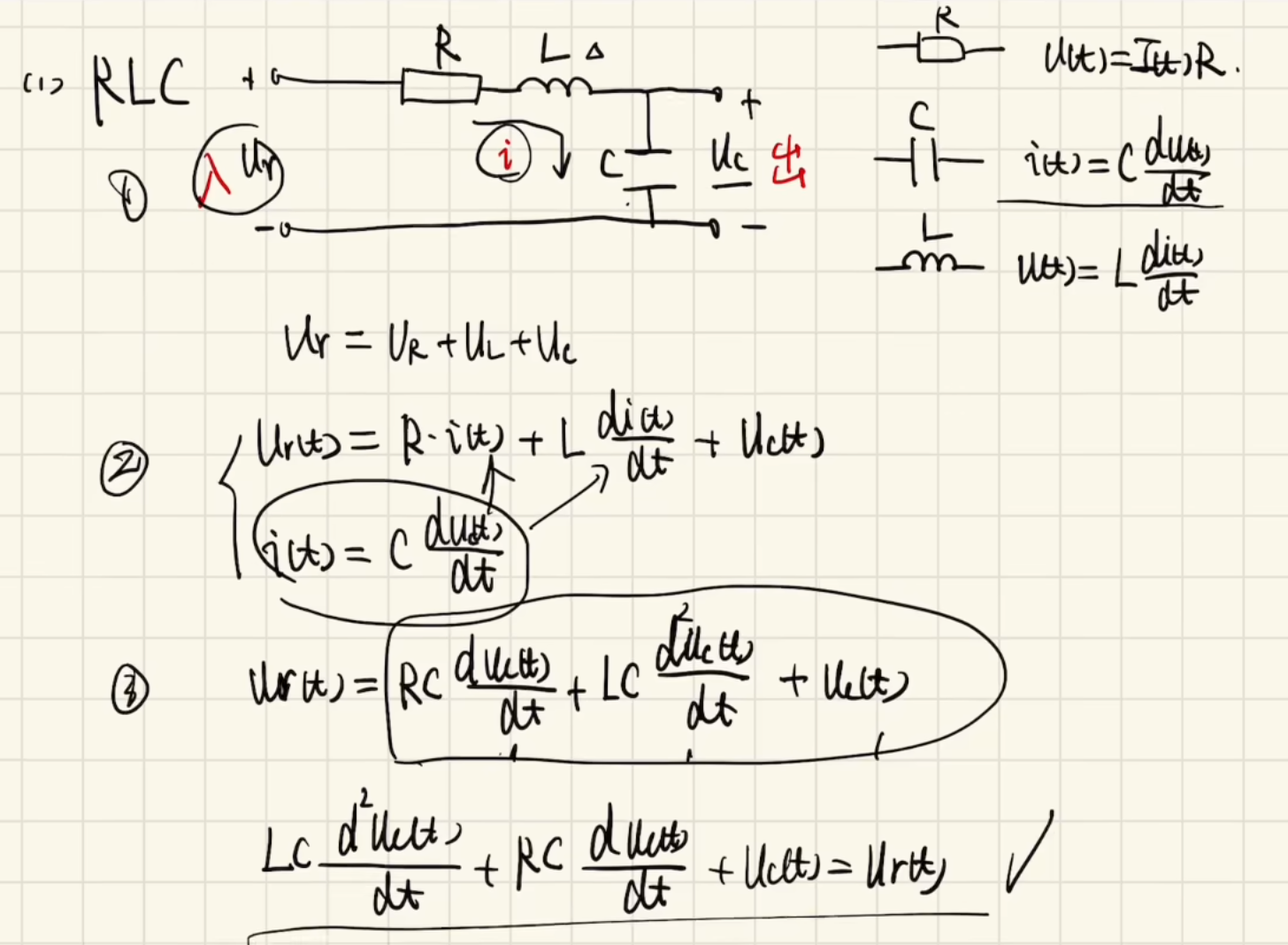
RLC模型：

描述由电阻（R）电感（L）和电容（C）组成的电路模型，其中输入是电压Ur，输出是电压Uc。

分析：
Ⅰ 输入输出非常明显是Ur和Uc
Ⅱ 寻找电压之间的分压关系，显然是总压分配给了RL和C，因此 $U_{r}=U_{R}+U_{L}+U_{C}$ ；
接着，由电容的电流-电压关系得到 $i(t) = C \frac{d u_C(t)}{dt}$ ；
由电感的电压-电流关系得到 $u_L(t) = L \frac{d i_L(t)}{dt}$ 。
Ⅲ 为了得到Ur与Uc的关系，要将中间变量 $U_{R}$ $U_{L}$ 利用Ⅱ的式子消去，最终得到③式。
最后整理为输出在左，输入在右，降幂排列的标准式。

机械-位移模型：

描述在力的作用下，物体的位移随时间变化关系的模型，其中输入是电压F(t)，输出是位移x。

分析：
Ⅰ 输入输出明显是F(t)、x(t)。
Ⅱ 通过力的作用效果对施加的力进行分配，分别起到影响加速度、影响阻尼、影响弹力的效果，因此 $F(t) = m \ddot{x}(t) + f \dot{x}(t) + k x(t)$ 。
Ⅲ 最后整理为输出在左，输入在右，降幂排列的标准式。

这两个例子给我们一个建立方程的思想——
分配思想：
例一，输入电压分配给了电容电阻和电感；
例二，力的效果引起了了加速度变换、阻尼和弹力；
将输入按效果或物理定律分配在各物理量上，再通过研究各物理量关系完成消元。

接着提出一个非常有用的研究策略，

相似系统：

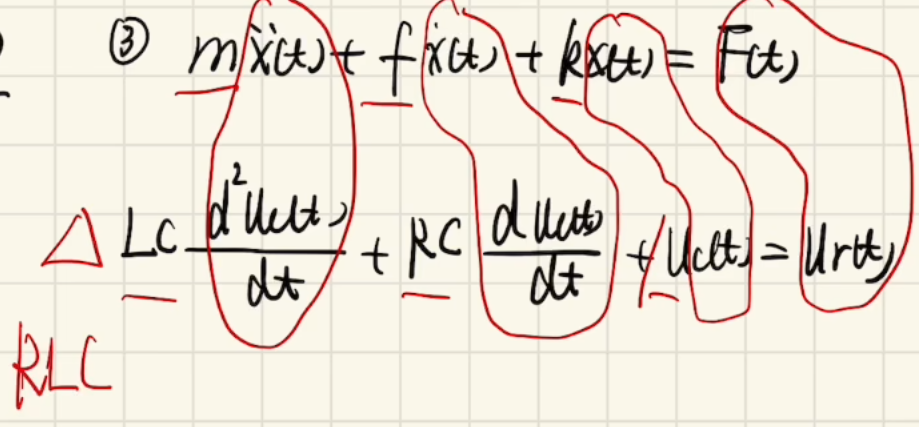
通过对比RLC模型和阻尼弹簧系统的微分方程，我们发现其每一项都一一对应。
因此我们可以通过研究RLC电路达到研究弹簧阻尼系统的规律，也就是说，可以将一个极其困难观测的模型等效为一个可观测的系统进行研究。

我们现在已经弄清楚了有哪些系统，以及如何构建一个微分方程来描述系统，并扩展了一种方程构建思想以及一种等效的系统研究方式。

我们发现，这样的微分方程虽然能直观描绘输入输出关系，但含有高次项，是极其难解的，因此我们考虑进行拉普拉斯变换，从而求解。

拉普拉斯变换

（圣经：“拉普拉斯变换是沟通时域与频域的桥梁。”）（时域频域可当作集合A、B，暂不用理解）

我们看如下两个函数

Ⅰ $\dot{f}(t)+3f(t)=0$

Ⅱ $sF(s)-F(0)+3F(s)=0$

Ⅰ式中求解f(t)显然有难度，因为其有导数项。

Ⅱ式则可以直接得到 $F(s)=\frac{F(0)}{s+3}$ ，简单好算。

其实，Ⅱ式就是Ⅰ式经过拉普拉斯变换后是式子，Ⅰ式是时域中的微分方程，Ⅱ式则是频域中的代数方程。当我们解出Ⅱ式的方程后，可以通过拉普拉斯逆变换，得到其在时域中的解。

观察得知，拉普拉斯变换最重要的一步就是解决了难处理的微分项。

拉普拉斯变换定义

那么拉氏变换具体如何实现呢？

我们引出拉普拉斯变换的定义：

$f(t)\overset{L}{\rightarrow}F(s)$

$F(s)=\int_{0}^{\infty }f(t)e^{-st}dt$

即，拉氏变换后的方程F(s)就是对原函数乘以 $e^{-st}$ 并在（0，+∞）上积分。

不如体会一下常见输入的拉氏变换的什么样的吧~

求如下输入分段函数（阶跃频率）后输出的拉氏变换：

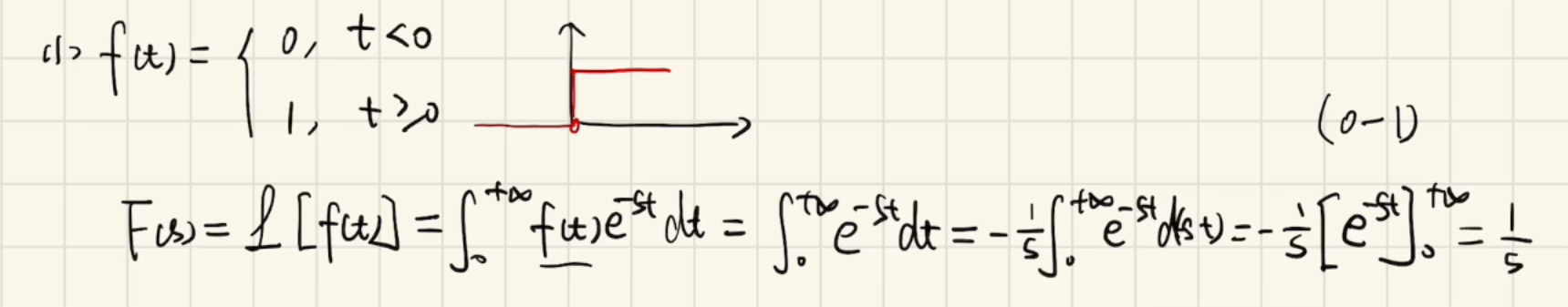
求线性输入后输出的拉氏变换：

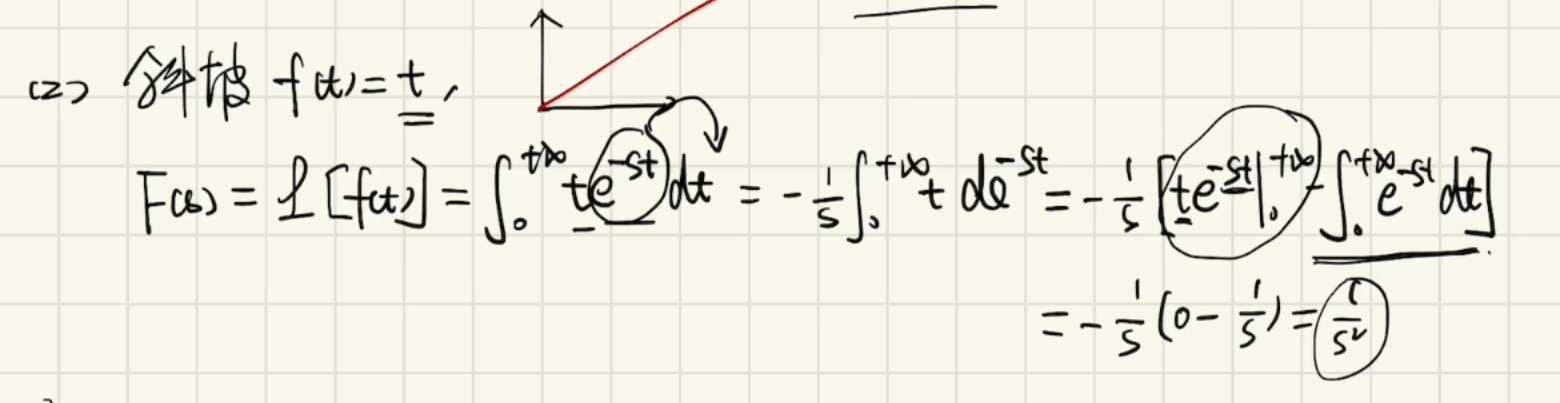
求加速度信号输入后输出的拉氏变换：

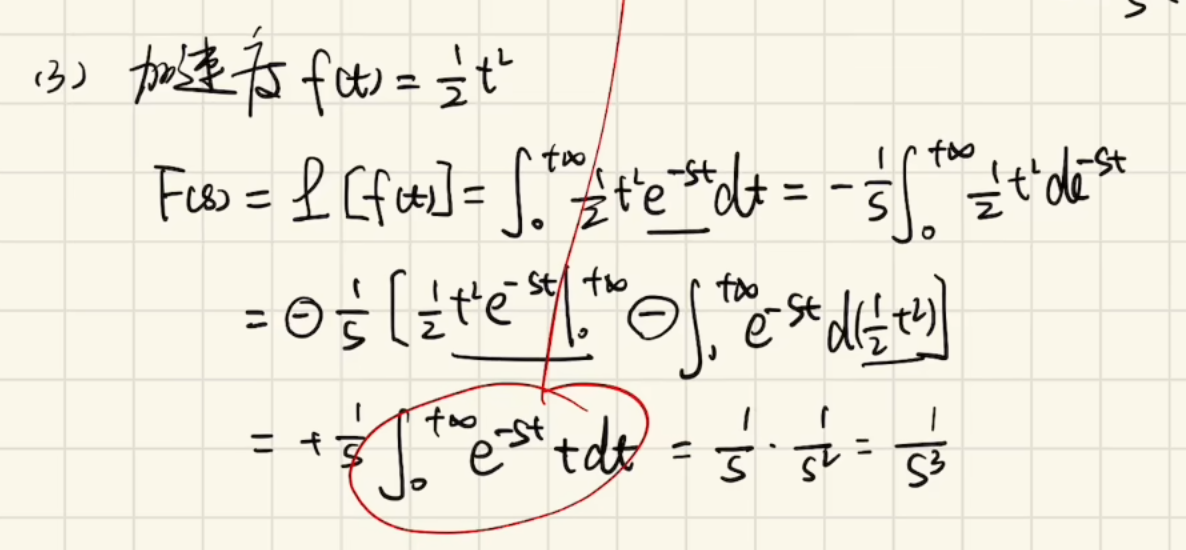
求脉冲信号输入后输出的拉氏变换：

常见拉氏变换对

我们将常用的输入进行拉氏变换，方便查表使用。

他们就像我们学微积分的常见积分表一样，需要熟记，前几个要能自行推证。

微分方程形式——时间域 f(t)	代数形式——拉普拉斯域 F(s)
δ(t)——脉冲函数	1
u(t)——阶跃函数	$\frac{1}{s}$
f(t)=t——线性函数	$\frac{1}{s^2}$
$f(t)=\frac{1}{2}at^2$ ——加速度函数	$\frac{1}{s^3}$
$f(t)=e^{-\alpha t}$	$\frac{1}{\alpha + s}$
$\frac{1}{n!} t^n e^{-\alpha t}$	$\frac{1}{(s + \alpha)^{n+1}}$
$\sin(\omega t)$	$\frac{\omega}{s^2 + \omega^2}$
$\cos(\omega t)$	$\frac{s}{s^2 + \omega^2}$
$e^{-\alpha t} \sin(\omega t)$	$\frac{\omega}{(s + \alpha)^2 + \omega^2}$
$e^{-\alpha t} \cos(\omega t)$	$\frac{s + \alpha}{(s + \alpha)^2 + \omega^2}$

拉氏变换的性质

1）线性性：

拉氏变换由于是积分运算，积分满足叠加性和成倍数性，因此具有线性性。

2）位移性质：（作用于变换量）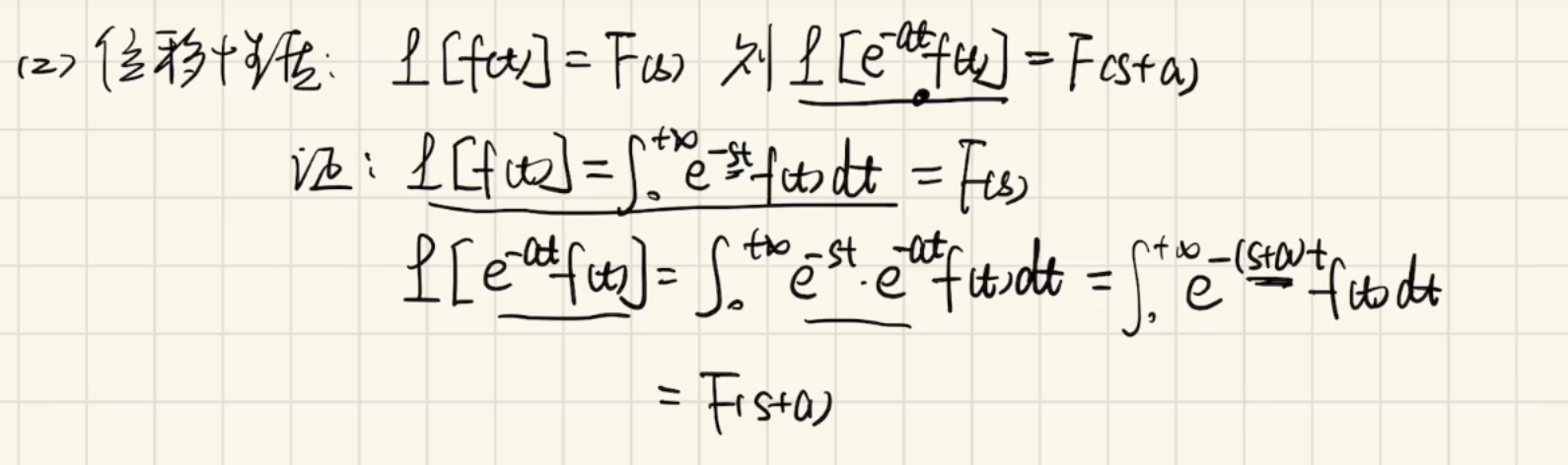

速记：内乘 $e^{-at}$ ，输出F(s+a)。

3）延时性质：(作用于自变量t-τ)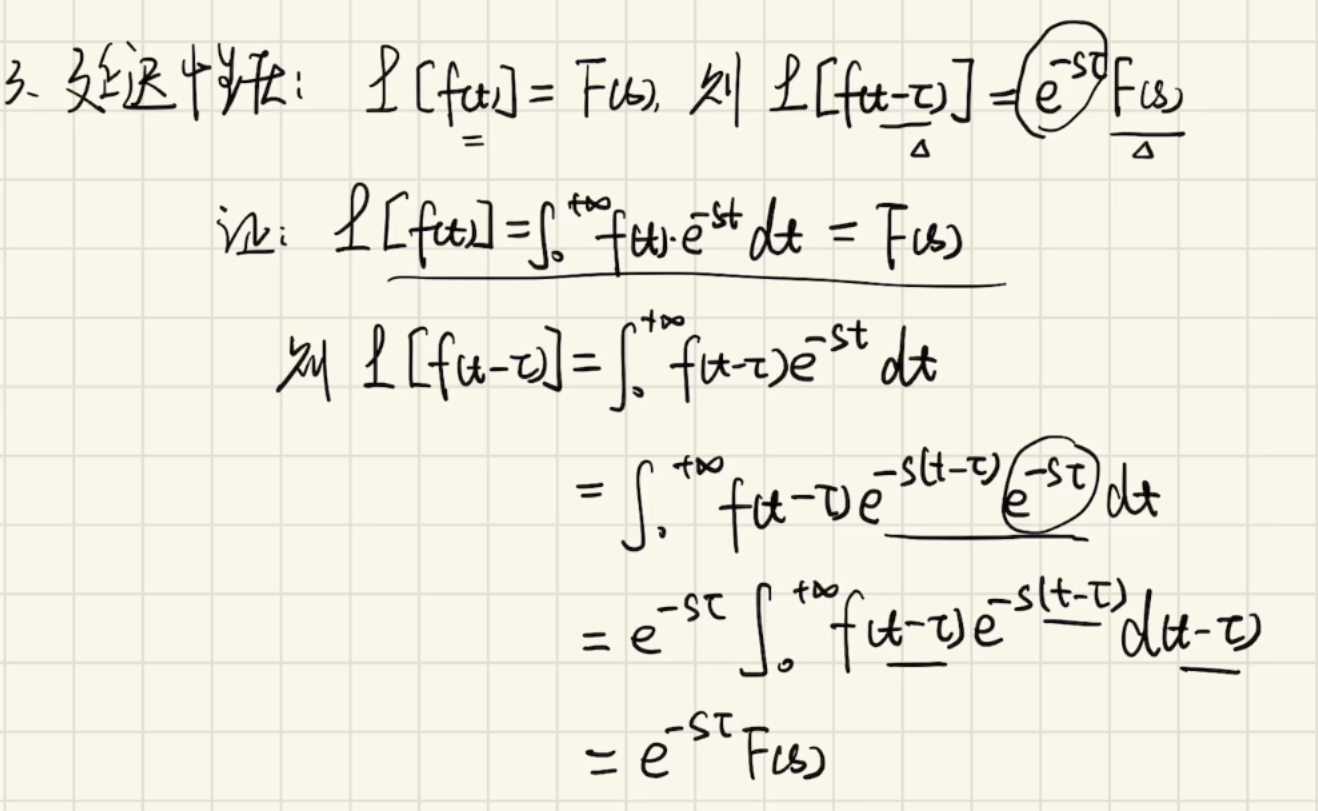

速记：比如一个阶跃信号，延迟了τ，那么利用延迟性质和阶跃信号的拉氏变换，延迟多少就乘 $e^{-s\tau}$ 。

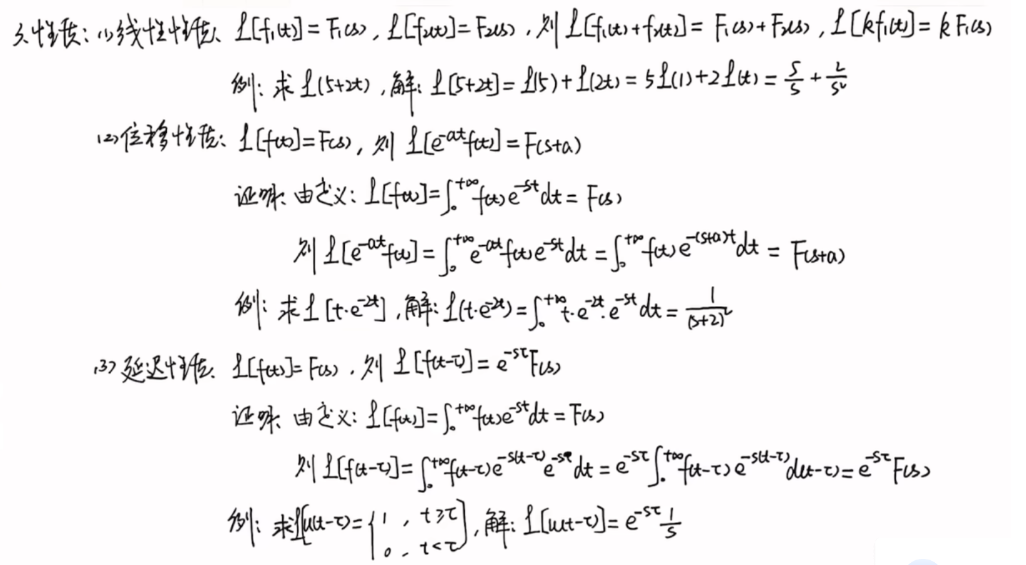
定理：

如果把刚刚的拉氏变换对比作微积分的常见积分表的话，这三大定理就好比直接积分法、换元积分法、分部积分法的作用，能帮我们解决绝大多数拉氏变换的问题。

以下定理重要程度微分》积分》终值，请自行再推导一遍微分定理，这样才能理解为什么高阶微分可以这样展开。此外，最好每个定理都能自行推证，也是个练习微积分的机会，包括分部积分法、变上限积分等。

微分定理：（解决高阶微分项）

由 $F(s) = \mathcal{L}\{f(t)\} = \int_{0}^{\infty} e^{-st} f(t) dt$ 可以得到：

$\mathcal{L}\{f'(t)\} = sF(s) - f(0)$ ，即，一阶微分的拉普拉斯变换可以化简为sF(s)-f(0)。

归纳法得到：

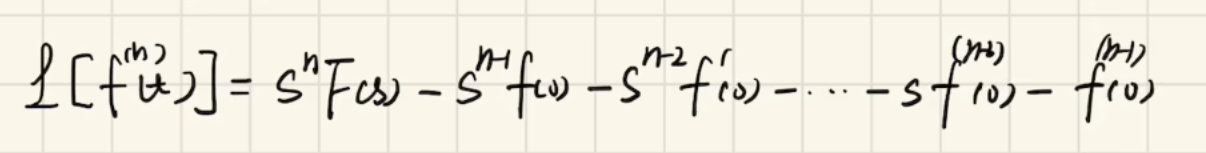
$\mathcal{L}\left[f^{(n)}(t)\right] = s^n F(s) - s^{n-1} f(0) - s^{n-2} f'(0) - \cdots - s f^{(n-2)}(0) - f^{(n-1)}(0)$

有了他，我们就可以解决所有含高阶微分项的微分方程的拉氏变换了！

积分定理：（解决积分项）

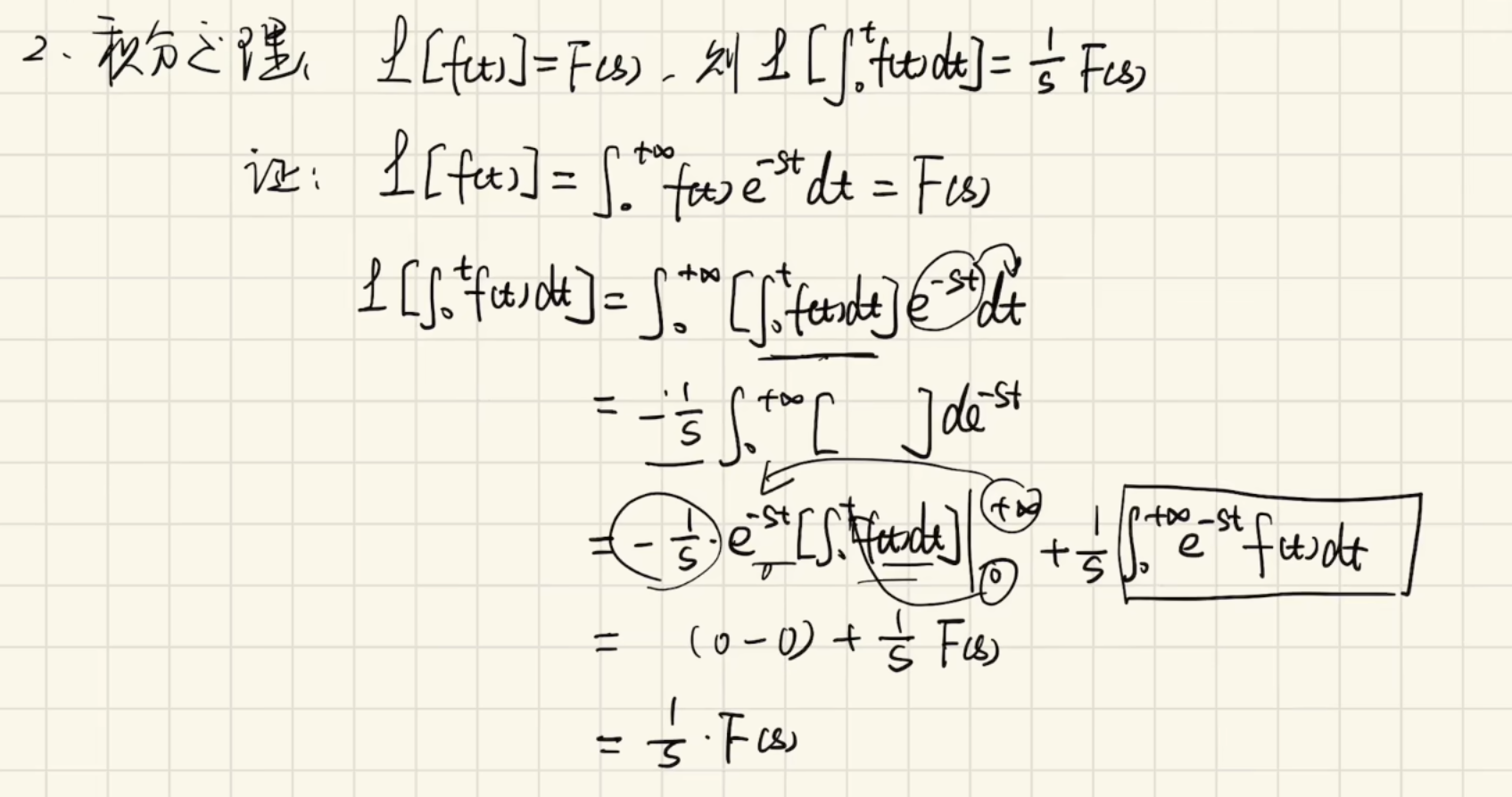
终值定理：

对于一个函数f(t)，如果它的拉普拉斯变换为 F(s)，那么根据终值定理，时域与频域同时取极限，就可以得到：

$\lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s)$

这意味着，如果我们知道 f(t) 的拉普拉斯变换 F(s)，就可以通过计算 sF(s) 在 s 趋近于 0 时的极限来找到 f(t) 在 t 趋近于无穷大时的极限值。

证明：

这个式子既包含f(t)，也包含F(s)变量，就要找前面某个也包含f(t)和F(s)的式子推导。回忆微分定理： $\mathcal{L}\{f'(t)\} = sF(s) - f(0)$

分别对左右两边取极限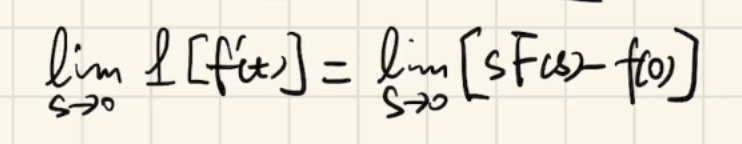

对于左边：

积分出来就是 $\left. f(t) \right|_{0}^{+\infty}=\lim_{t \to +\infty} f(t) - f(0)$

对于右边：

因此结合左右的极限有 $\lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s)$ ，即终值定理。

他们的作用：有了这三个定理，我们就可以对微分方程那些不友好的微分项、积分项进行拉氏变换了！

以上，我们掌握了如何将微分方程转化为一个代数方程的形式，大大简化了计算难度。然而，我们很难通过代数方程的解，直接观察系统的瞬态响应或稳态响应，特别是其瞬态响应特性，如上升时间、峰值时间和过冲等，也无法画出动态输出响应-时间图，因此往往我们需要将解反拉氏变换回时域进行分析。

反拉氏变换：

反拉氏变换，即将频域的代数方程转化为时域的微分方程。

我们前面得到了拉普拉斯变换对表，从上至下是拉氏变换，从下至上就是反拉氏变换了，记作 $\mathcal{L}^{-1}$

比如下例，对 $\frac{1}{s+\alpha}$ 反拉氏变换，可查表得知是 $e^{-\alpha t}$ ，一般不会考察超越这个数对表以外的反拉氏变换。

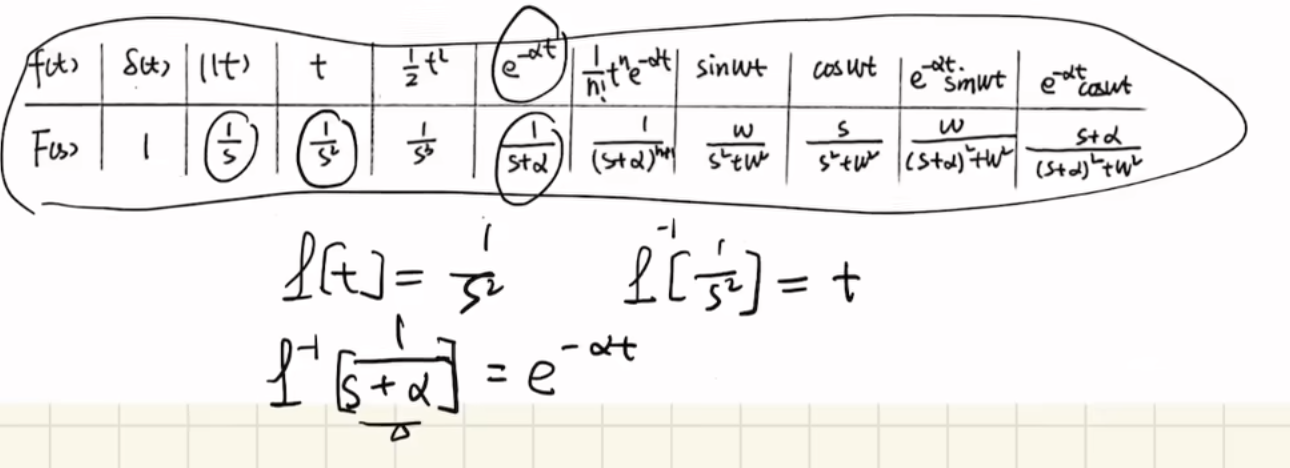
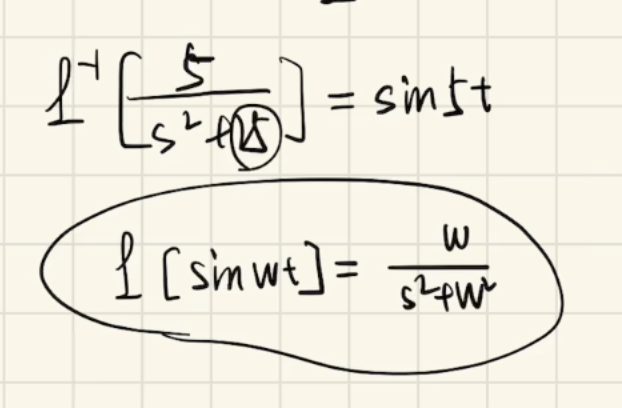
拉氏变换与反变换解线性微分方程

至此为止，如何求微分方程在微分形式的解的问题就变得通透了，先拉氏变换得到容易求解的代数方程，接着将解进行反拉氏变换得到微分形式的解，流程图如下。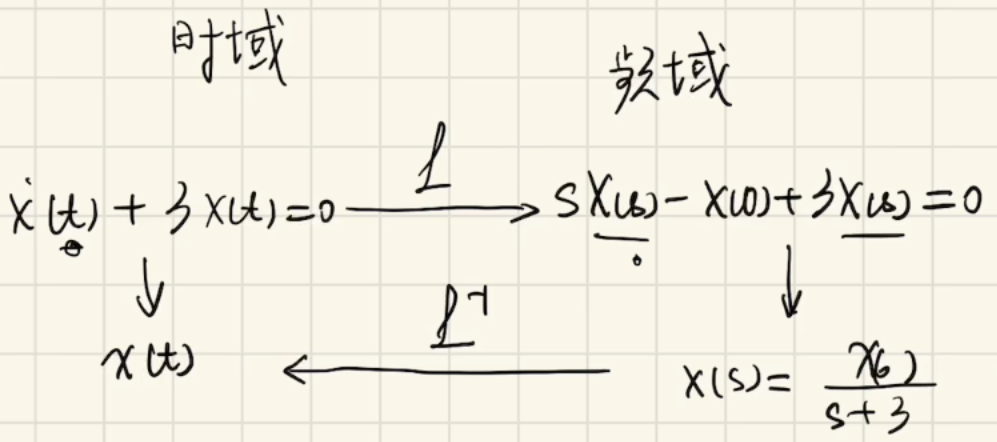

零初始条件

在完成含高阶微分的拉氏变换后，会遇到一件尴尬的事，出现了一堆消不掉的f(0)高阶导，怎么办呢？

为了简化计算，我们引入零初始条件——即在系统启动瞬间，所有高阶物理参量全为零。

这很好理解，汽车在启动前位移、速度、加速度都为零；电路中的电容电压、电感电流在电源接通瞬间也为零。

于是，这些高阶导全都归零了：

$f(0) = f'(0) = f''(0) = \cdots = f^{(n)}(0) = 0$

一般都会基于零初始条件进行分析，因为我们研究的是时不变系统，只要给定了输入，时间如何变化，输出都是固定的！

切记，只有在零处是条件时，才可以将零处的高阶导赋为0！！！

这一节介绍了系统分类、拉氏变换、如何用拉氏变换解决微分方程、反拉氏变换、如何用反拉氏变换得到微分形式的解，以及零初始条件的作用。

以上就是本节最重要的部分了，重在理解，而不是刷题。非专业课可以下一节了。
下面是在求解的时候常见的手段：

应试部分

裂项法

我们常常会获得这样的待化简方程，求其在微分形式的解/进行反拉氏变换。

$X(s) = \frac{2s + 7}{s(s + 4)(s + 1)}$

发现分子是多项式相乘，在常见拉氏变换数对表中找不到怎么办？

那就往和其最相似的形式靠——裂项

$\frac{1}{\alpha + s} ~$ ~ $f(t)=e^{-\alpha t}$ 我们总是记得的，通过裂项可以将分母化为：

$\frac{C_1}{s} + \frac{C_2}{s+4} + \frac{C_3}{s+1}$

接着就有两种常用的技巧

Ⅰ乘在一起对照系数，比较得到C1 C2 C3，显然项比较多或次数较高就麻烦了。

Ⅱ 极点带入法

$\frac{C_1}{s} + \frac{C_2}{s+4} + \frac{C_3}{s+1}= \frac{2s + 7}{s(s + 4)(s + 1)}$

假设要求C1，如果能左右同乘s，再令s=0，就可以将C2 C3全消去了，只剩下C1=右边的式子

同理这么操作也可以得到C2 C3

$C_1 = \left. \frac{2s + 7}{(s+4)(s+1)} \right|_{s=0}$

$C_2 = \left. \frac{2s + 7}{s(s+1)} \right|_{s=-4}$

$C_3 = \left. \frac{2s + 7}{s(s+4)} \right|_{s=-1}$

而我们发现，乘以Cn分母后带入的点正好是使得这个多项式为零的值，我们称为极点，这就是极点带入法。

当然，这样仍然存在一个问题——分母如果重根，那么这样就只能求得一个解了：

$X(s)=\frac{5s + 7}{s(s + 2)(s + 3)}$

如何裂项呢？

我们考虑从最高次项裂到一次项（这也是微积分上的内容）

$\frac{5s + 7}{s(s + 2)(s + 3)^2} = \frac{C_1}{s} + \frac{C_2}{s + 2} + \frac{C_{31}}{(s + 3)^{3}} + \frac{C_{32}}{(s + 3)^2} + \frac{C_{33}}{s + 3}$

由于这个时候带入x=-3这个极点无法求得C32 C33，

$\frac{5s + 7}{s(s + 2)(s + 3)^2} \cdot (s + 3)^2 =$

$\frac{C_1}{s} \cdot (s + 3)^2 + \frac{C_2}{s + 2} \cdot (s + 3)^2 + C_{31} + C_{32}(s + 3) + C_{33}(s + 3)^2$

因此我们考虑对其求导，再带入极点即可：

$C_{32} = \left. \frac{d}{ds} \left( \frac{5s + 7}{s(s + 2)} (s + 3)^2 \right) \right|_{s = -3}$

$C_{33} = \left. \frac{d^2}{ds^2} \left( \frac{5s + 7}{s(s + 2)} (s + 3)^2 \right) \right|_{s = -3}$

总结

分母不重根 Cn=乘以各项后带入极点。

分母重根，先乘以最高次，否则消不掉；
再对高次项求导，带入极点。

习题集：

写在后面：

很开心你能耐着性子读到这里，很荣幸能将我的三脚猫知识分享给大家。

星马也是小白，因此更懂小白的心思。这篇文章也还有很多不足之处，或是纰漏，希望你发现了及时在评论区提醒我呀~

（人工智能学院就是每周四五天满课的啦，最近期中考试，更新基本随缘~）

别丢收藏夹吃灰啦好嘛~

星马是刚入门的大菜比，有错望指正，有项目可以带带我。

DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

【机器人导航】基于A_Satr算法模拟网格地图多机器人导航附Matlab代码

针对多机器人在网格地图环境中导航面临的路径冲突频发、任务分配不合理、协同效率低等问题，提出一种基于改进 A算法的多机器人协同导航方案。该方案采用栅格法构建环境模型，通过改进 A算法为单机器人规划局部最优路径，引入时间窗机制与优先级分配策略解决多机器人路径冲突，结合任务距离与机器人性能实现动态任务分配，最终实现多机器人无碰撞、高效率的协同导航。