机器人运动学笔记

SDH和MDH会不一样，主要的区别在于SDH中坐标系在连杆末端，MDH中坐标系在连杆首端。虽然这里只是给出z轴，但是由于后面原点位置不同，所以二者z轴也不同。

abcd51685168

218人浏览 · 2024-06-20 05:00:00

abcd51685168 · 2024-06-20 05:00:00 发布

一、建模

参考资料：https://zhuanlan.zhihu.com/p/137960186

1、三维模型和连杆、关节定义

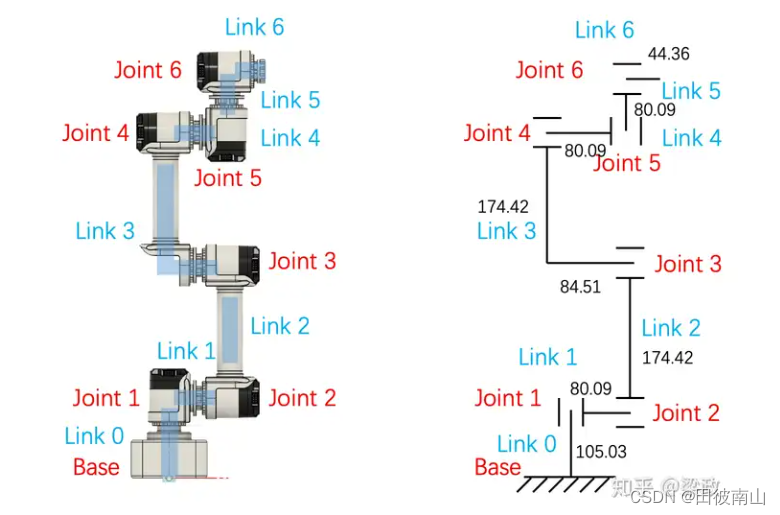
在这里插入图片描述

2、设置z轴

SDH和MDH会不一样，主要的区别在于SDH中坐标系在连杆末端，MDH中坐标系在连杆首端。虽然这里只是给出z轴，但是由于后面原点位置不同，所以二者z轴也不同。

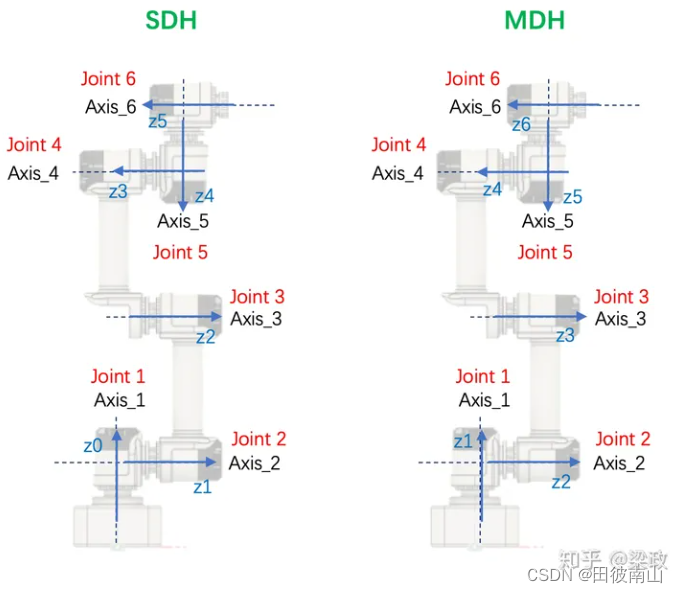
2、设置原点和x轴

方法	SDH	MDH
原点	i和i-1的交线是i原点，如果不想交用公垂线与i交点	i和i+1的交线是i原点，如果不想交用公垂线与i交点
x轴	指向i-1	指向i+1原点
添加	0坐标系	6坐标系
y轴	右手定则	右手定则

关于原点这块我的理解和资料上不同，不知道谁写错了

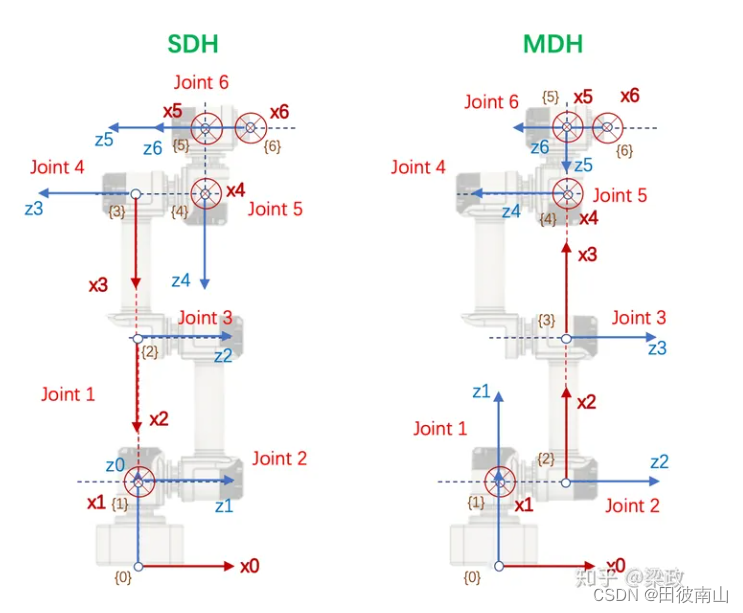
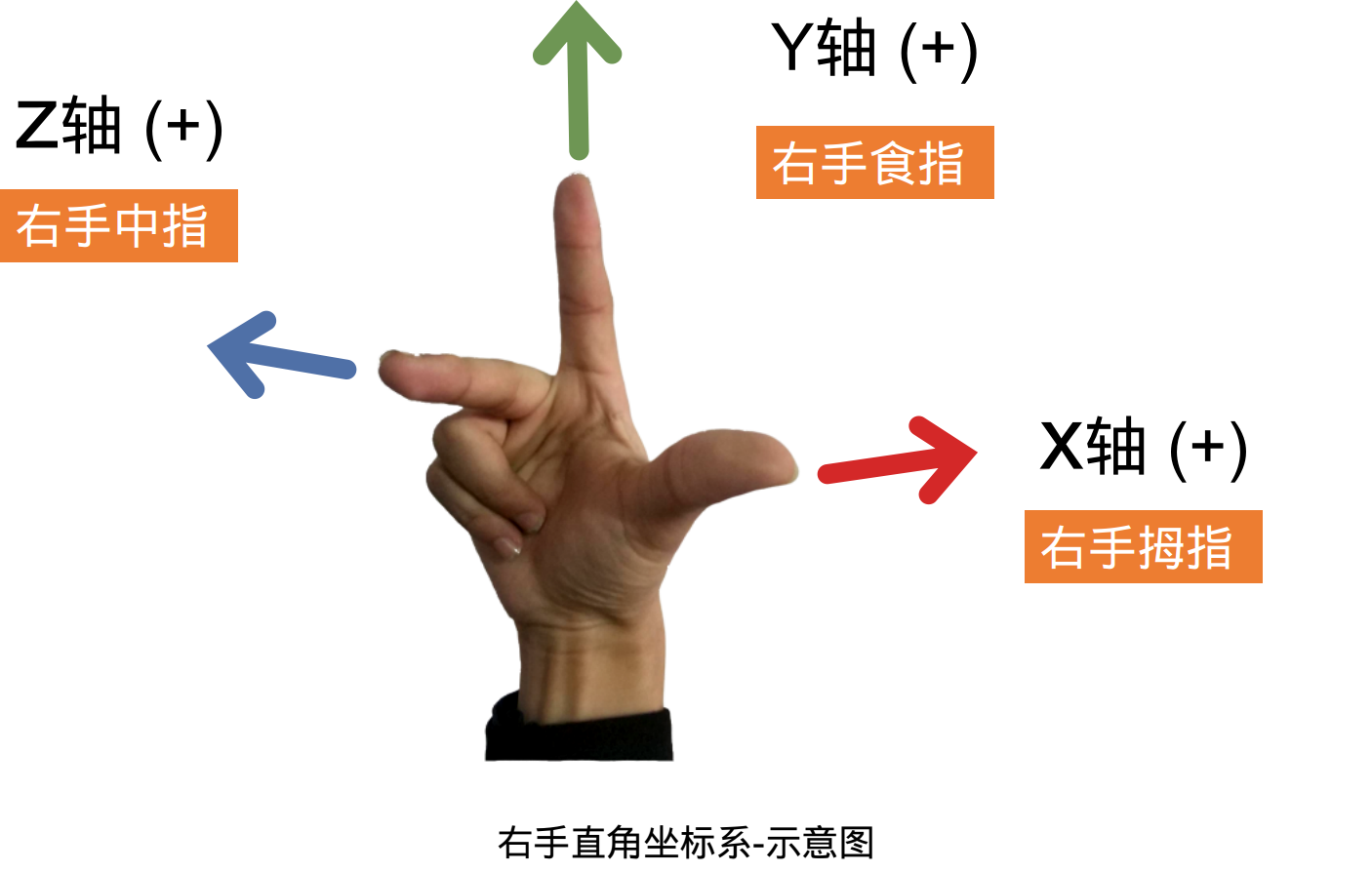
3、确定dh参数

SDH和MDH都是由前一坐标系移动到下一坐标系，写i行就是{i-1}到{i}
所有角度符合右手螺旋定则的是正方向
theta是绕z轴转使得x轴重合的角度，d是沿着z轴运动使得x轴重合的距离

（1）SDH

      θ 
     
    
      → 
     
    
      d 
     
    
      → 
     
    
      α 
     
    
      → 
     
    
      a 
     
    
   
     \theta\rightarrow d\rightarrow\alpha\rightarrow a 
    
   
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">θ</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">a</span></span></span></span></span><br> <img src="https://img-blog.csdnimg.cn/direct/73d86d7ac31e48e1972f07864320a5a7.png" alt="在这里插入图片描述"></li></ul>

（2）MDH

      α 
     
    
      → 
     
    
      a 
     
    
      → 
     
    
      θ 
     
    
      → 
     
    
      d 
     
    
   
     \alpha\rightarrow a\rightarrow\theta\rightarrow d 
    
   
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal" style="margin-right: 0.0037em;">α</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.4306em;"></span><span class="mord mathnormal">a</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal" style="margin-right: 0.0278em;">θ</span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 0.6944em;"></span><span class="mord mathnormal">d</span></span></span></span></span><br> <img src="https://img-blog.csdnimg.cn/direct/4f88550a2ffa4fb2b98e10b8aefb6cbd.png" alt="在这里插入图片描述"></li></ul>

（3）几何参数

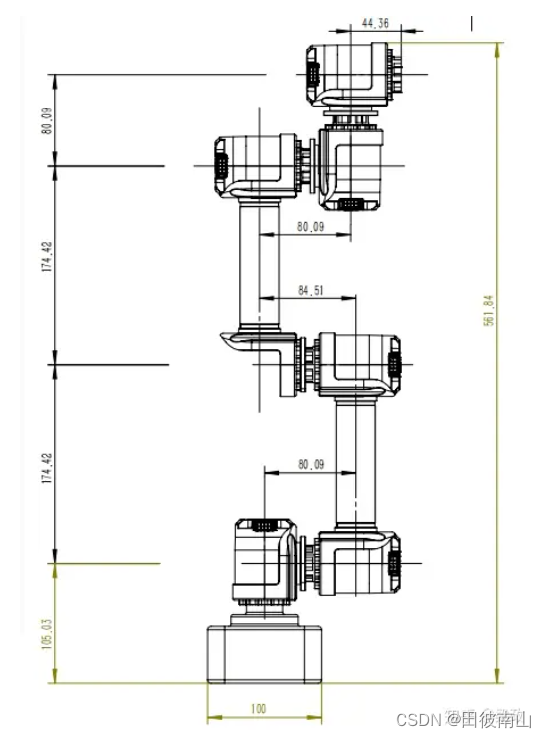
在这里插入图片描述

二、正运动学

资料：https://blog.csdn.net/subtitle_/article/details/130982929

1、齐次变换矩阵

可以以此计算所有的T，左上的3×3是三个轴，右侧是三维向量是原点坐标
标准DH的齐次变换矩阵
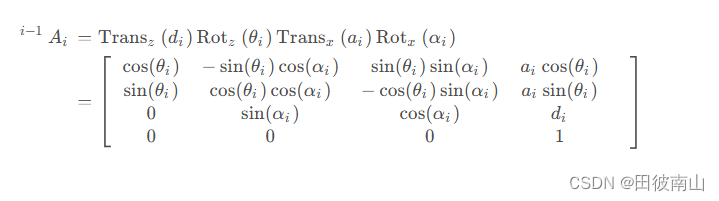
改进dh法的齐次变换矩阵

三、逆运动学

资料： https://blog.csdn.net/wh_STUDY/article/details/126862627
常用的方法有几何解法、代数解法和数值解法

1、pieper准则

如果一个机械臂的结构满足pieper准则，则有封闭解，即可以获得用公式表达的解

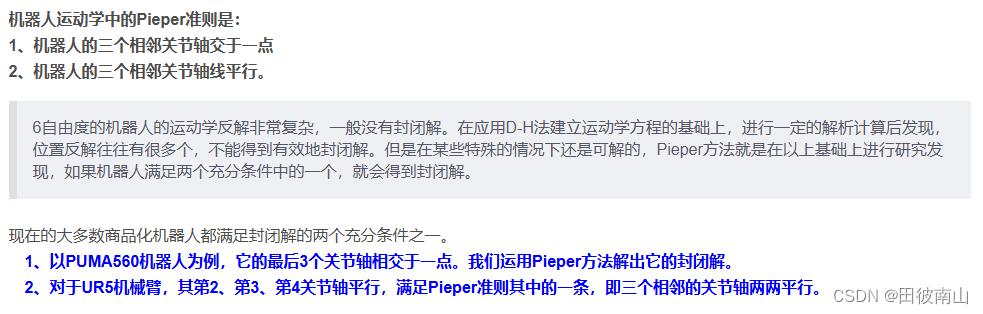
2、几何解

几何解直接看参考连接中举得案例，一般很少使用

3、代数解

参考资料：工业用六轴机械臂的建模与仿真_卢锐

3.1 改进dh建模

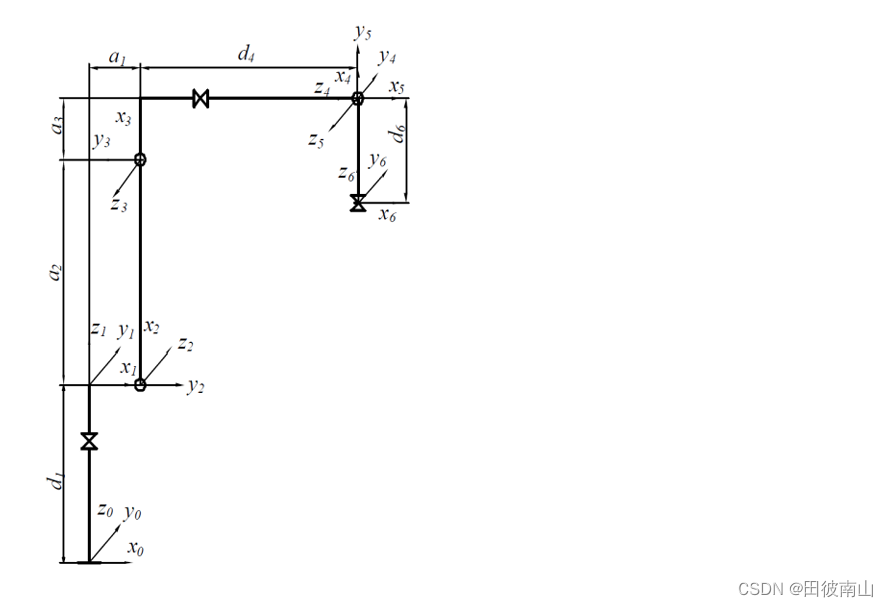
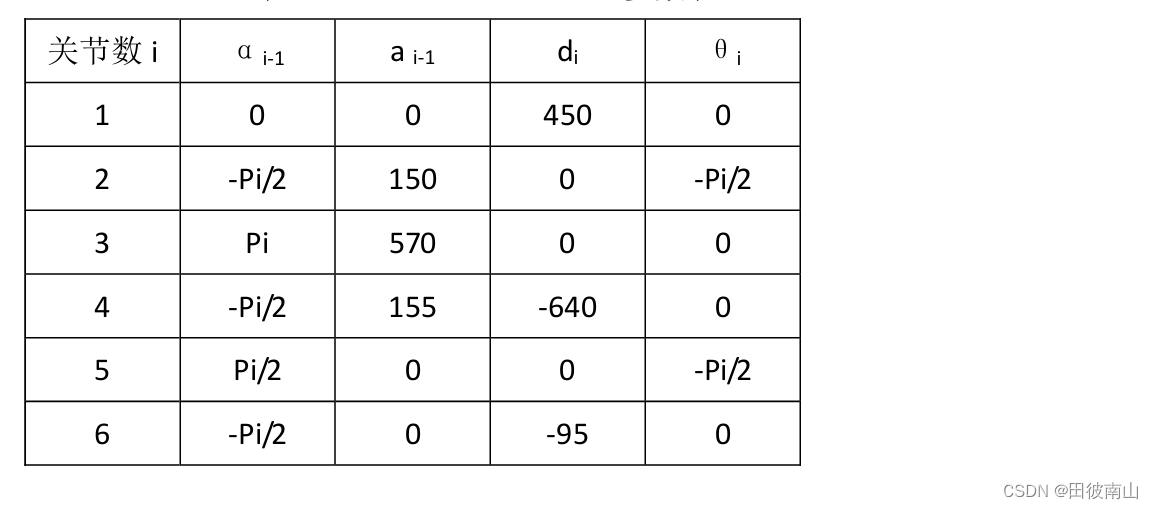
在这里插入图片描述

3.2 求代数逆解

利用的就是齐次变换矩阵的相乘(一般是在左侧的上下标)

        A 
       
      
        6 
       
      
        0 
       
      
     
       = 
      
      
      
        A 
       
      
        1 
       
      
        0 
       
      
      
      
        A 
       
      
        2 
       
      
        1 
       
      
      
      
        A 
       
      
        3 
       
      
        2 
       
      
      
      
        A 
       
      
        4 
       
      
        3 
       
      
      
      
        A 
       
      
        5 
       
      
        4 
       
      
      
      
        A 
       
      
        6 
       
      
        5 
       
      
     
    
      A^0_6 = A^0_1A^1_2A^2_3A^3_4A^4_5A^5_6 
     
    
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.1111em; vertical-align: -0.247em;"></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">6</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">0</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1.1111em; vertical-align: -0.247em;"></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">0</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">5</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">6</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">5</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></li><li>求<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
  
   
    
     
     
       θ 
      
     
       1 
      
     
    
   
     \theta_1 
    
   
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.8444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right: 0.0278em;">θ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3011em;"><span class="" style="top: -2.55em; margin-left: -0.0278em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span><br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml"> 
   
    
     
      
       
       
         A 
        
       
         1 
        
       
         0 
        
       
       
       
         − 
        
       
         1 
        
       
      
      
      
        A 
       
      
        6 
       
      
        0 
       
      
     
       = 
      
      
      
        A 
       
      
        2 
       
      
        1 
       
      
      
      
        A 
       
      
        3 
       
      
        2 
       
      
      
      
        A 
       
      
        4 
       
      
        3 
       
      
      
      
        A 
       
      
        5 
       
      
        4 
       
      
      
      
        A 
       
      
        6 
       
      
        5 
       
      
     
    
      {A^0_1}^{-1}A^0_6 = A^1_2A^2_3A^3_4A^4_5A^5_6 
     
    
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.3151em; vertical-align: -0.247em;"></span><span class="mord"><span class="mord"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">0</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 1.0681em;"><span class="" style="top: -3.317em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">−</span><span class="mord mtight">1</span></span></span></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">6</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">0</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2778em;"></span></span><span class="base"><span class="strut" style="height: 1.1111em; vertical-align: -0.247em;"></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">5</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.8641em;"><span class="" style="top: -2.453em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">6</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">5</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span><br> 令两侧的（1,4）和（2,4）分别相等，依次求解其他角度，最终会有8组解</li></ul>
            </div>