基于蒙特卡洛法的电动汽车充电负荷计算matlab程序
目录一、充电概率分布二、日行驶里程三、无序充电负荷模型四、蒙特卡洛法分析一、充电概率分布代码如下:us=17.6;ds=3.4;fs1=@(x)1/(ds*(2*pi)^0.5).*exp(-(x-us).^2./(2*ds^2));%us-12~24fs2=@(x)1/(ds*(2*pi)^0.5).*exp(-(x+24-us).^2./(2*ds^2));%0~us-12xs1=lins
·
目录
一、充电概率分布

![]()
![]()
代码如下:
us=17.6;ds=3.4;
fs1=@(x)1/(ds*(2*pi)^0.5).*exp(-(x-us).^2./(2*ds^2));%us-12~24
fs2=@(x)1/(ds*(2*pi)^0.5).*exp(-(x+24-us).^2./(2*ds^2));%0~us-12
xs1=linspace(0,24,N);
%xs_1=xs1(1:47);
%xs_2=xs1(48:200);
%fs_st=[fs2(xs_1) fs1(xs_2)];
fs_st=fs2(xs1).*(xs1<=us-12)+fs1(xs1).*(xs1>us-12);
s_st=trapz(xs1,fs_st); %计算整个区间概率密度的积分
fs_st=fs_st/s_st; %归一化概率密度
n=0;
while n<N
t=rand(1)*24;%生成[0,30]均匀分布随机数
if t<=us-12
ft_st=fs2(t)/s_st;
else
ft_st=fs1(t)/s_st;
end
r=rand(1); %生成[0,1]均匀分布随机数
if r<=ft_st %如果随机数r小于f(t),接纳该t并加入序列a中
n=n+1;
ts_rand(n)=t;%随机生成行驶里程
end
end
num=20; %分20个区间统计
[x2,c]=hist(ts_rand,num); %统计不同区间出现的个数
dc=200/num; %区间大小
x2=x2/N/dc; %根据统计结果计算概率密度得到结果如下图:
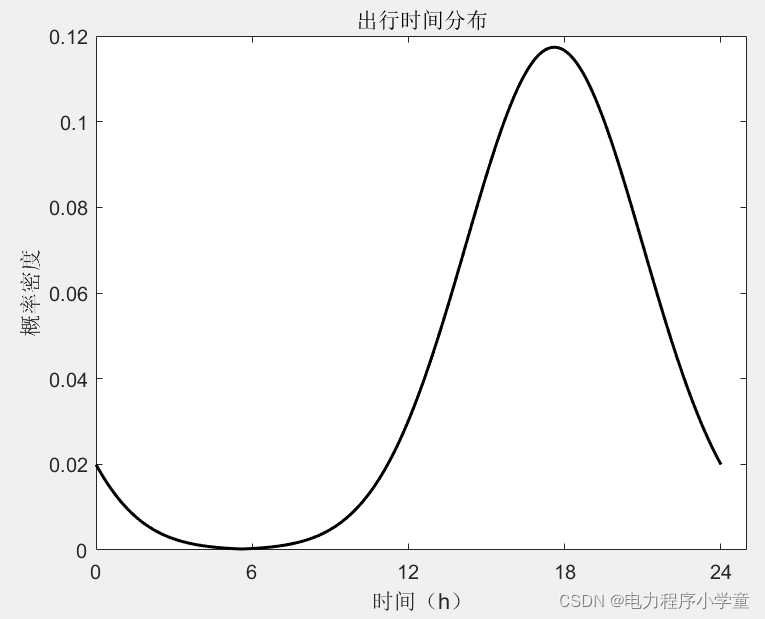

二、日行驶里程

ud=3.2;dd=0.88;
u0=0.205;
yt=0.9;%效率
cap=30;%容量
avg_v=40;%速度
avg_xh=0.2;%平均耗电量
pcd=5;%充放电功率
N=200;
%%%%%%%%%%%%%%%分布特性
f1=@(x)1./(x.*dd*(2*pi).^0.5).*exp(-(log(x)-ud).^2/(2*dd^2));
x1=linspace(0.1,200,N);
ff=f1(x1);
s=trapz(x1,ff); %计算整个区间概率密度的积分
ff=ff/s; %归一化概率密度
n=0;
while n<N
t=rand(1)*200;%生成[0,30]均匀分布随机数
f=f1(t)/s;
r=rand(1); %生成[0,1]均匀分布随机数
if r<=f %如果随机数r小于f(t),接纳该t并加入序列a中
n=n+1;
km_rand(n)=t;%随机生成行驶里程
end
end
%以上为生成随机数列的过程,以下为统计检验随机数列是否符合分布
num=20; %分20个区间统计
[x2,c]=hist(km_rand,num); %统计不同区间出现的个数
dc=200/num; %区间大小
x2=x2/N/dc; %根据统计结果计算概率密度
figure;
%bar(c,x2,1); hold on; %根据统计结果画概率密度直方图
plot(x1,ff,'k','lineWidth',1.5); %hold off; %根据公式画概率密度曲线
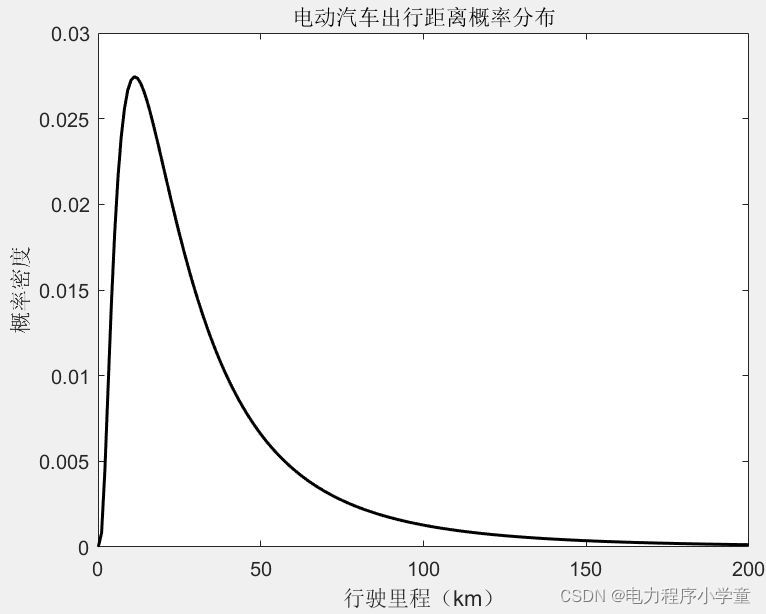
title('电动汽车出行距离概率分布');
xlabel('行驶里程(km)');
ylabel('概率密度');三、无序充电负荷模型


 四、蒙特卡洛法分析
四、蒙特卡洛法分析



通过模拟可以得到如下结果:
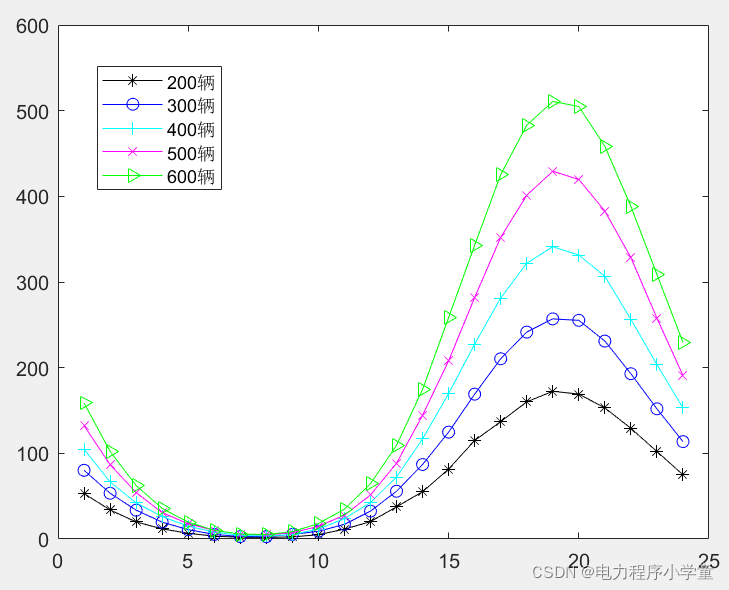
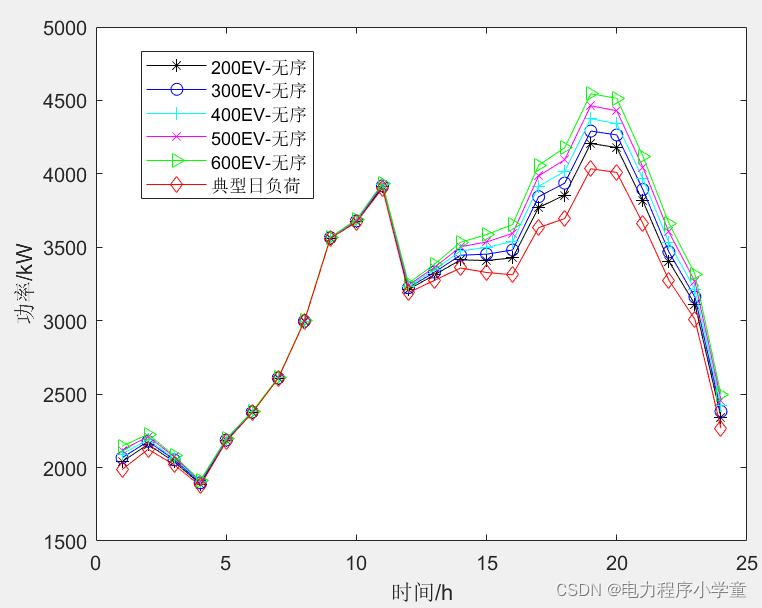

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容
 https://download.csdn.net/download/zhangxd212489/72899261?spm=1001.2014.3001.5503
https://download.csdn.net/download/zhangxd212489/72899261?spm=1001.2014.3001.5503





所有评论(0)