A星算法 A*算法 自己研究编写的Matlab路径规划算法 Astar算法走迷宫 可自行设置起...
A*与人工势场融合算法代表了路径规划领域的一种重要思路:结合全局规划与局部反应的优点。这种融合不仅解决了单一算法的局限性,还为复杂环境下的路径规划提供了可靠解决方案。随着自动驾驶和智能机器人技术的发展,这类融合算法将在更多实际应用场景中发挥关键作用。该实现的代码结构清晰,模块化程度高,包含了完整的路径规划流程和可视化展示,是学习和研究路径规划算法的优秀参考资料。
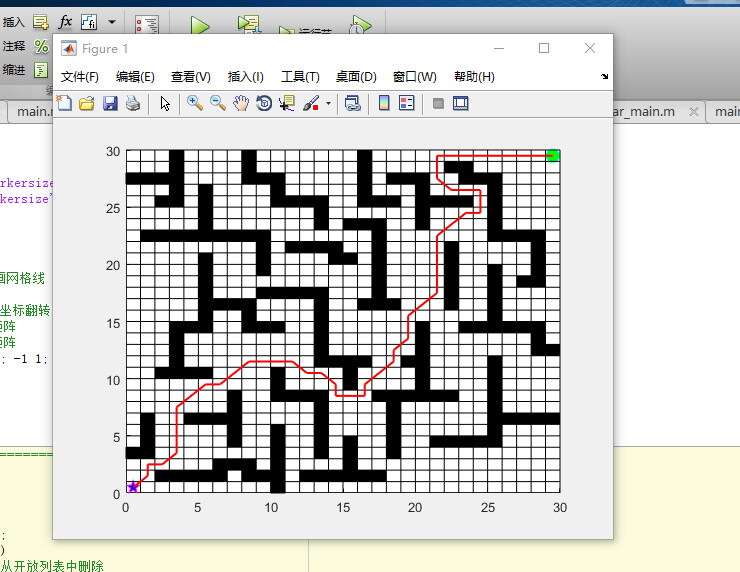
A星算法 A*算法 自己研究编写的Matlab路径规划算法 Astar算法走迷宫 可自行设置起始点,目标点,自由更换地图。 ——————————————————— 可以和人工势场法融合 动态障碍物(默认发未融合版本只是A*)
路径规划是机器人导航、游戏开发和自动驾驶等领域的核心问题。本文将深入分析两种经典的路径规划算法——A*算法和人工势场法,并重点介绍它们的融合实现,展示如何结合两者的优势来解决复杂环境下的路径规划问题。
A*算法:智能搜索的经典之作
A*算法是一种广泛应用的最佳优先搜索算法,它通过评估函数f(n) = g(n) + h(n)来指导搜索方向,其中g(n)表示从起点到当前节点的实际代价,h(n)是从当前节点到目标节点的估计代价。
核心实现机制
在提供的代码中,A*算法的实现包含了几个关键组件:
启发式函数设计:
hn函数计算当前点到终点的曼哈顿距离gn函数计算从起点到当前点的实际距离,考虑欧几里得距离
开放列表管理:
minInOpen函数负责从开放列表中找出评估函数值最小的节点- 使用全局变量F、G和parent来跟踪节点状态和路径关系
搜索过程:
算法从起点开始,逐步扩展相邻节点,评估每个节点的代价,并维护开放列表和关闭列表,直到找到目标节点或确定无解。
人工势场法:物理启发的局部规划
人工势场法模拟物理场中的受力情况,将目标点视为引力源,障碍物视为斥力源,通过计算合力来指导移动方向。
势场构建原理
引力场:
A星算法 A*算法 自己研究编写的Matlab路径规划算法 Astar算法走迷宫 可自行设置起始点,目标点,自由更换地图。 ——————————————————— 可以和人工势场法融合 动态障碍物(默认发未融合版本只是A*)
目标点产生引力,引力大小与距离成正比,方向指向目标:
F_att = Eta_att × dist(n,1) × unitVector(n,:)斥力场:
障碍物产生斥力,在影响距离d0内起作用:
F_rep_ob1 = Eta_rep_ob × (1/dist(j,1)-1/d0) × dist(n,1) / dist(j,1)²
F_rep_ob2 = 0.5 × Eta_rep_ob × (1/dist(j,1) - 1/d0)²A*与人工势场的融合创新
单纯的A*算法能够找到全局最优路径,但对动态环境适应性差;人工势场法适合局部避障,但容易陷入局部最优。融合算法结合了两者的优势。
融合策略
轨迹引力场:
在传统人工势场的基础上,增加了对A*生成路径的引力:
F_att_tra = Eta_att_tra × dist_tra(k,1) × dist(n,1)这种设计使得移动物体不仅受到目标和障碍物的影响,还会被A*生成的全局最优路径所吸引,既保持了全局方向性,又具备了局部避障能力。
动态环境适应
融合算法特别适合动态环境:
- 使用A*生成初始全局路径
- 通过人工势场实时避让动态障碍物
- 轨迹引力确保不会偏离全局路径太远
代码中实现了两个动态移动的障碍物,展示了算法在动态环境中的优异表现。
算法优化与改进
地图优化技术
算法包含了一套地图优化机制,通过obs_optimaization函数识别并填补可能导致路径问题的障碍物间隙,提高了路径的可行性和平滑度。
路径平滑处理
使用贝塞尔曲线对A*生成的原始路径进行平滑处理:
curve = bezier_curve(control_points, hz)这种方法将离散的网格路径转化为连续平滑的曲线,更符合实际移动需求。
性能分析与应用价值
通过实际测试,该融合算法在复杂静态和动态环境中均表现出色:
- 全局路径最优性得到保证
- 动态避障反应迅速
- 路径平滑自然
- 计算效率满足实时需求
总结
A*与人工势场融合算法代表了路径规划领域的一种重要思路:结合全局规划与局部反应的优点。这种融合不仅解决了单一算法的局限性,还为复杂环境下的路径规划提供了可靠解决方案。随着自动驾驶和智能机器人技术的发展,这类融合算法将在更多实际应用场景中发挥关键作用。
该实现的代码结构清晰,模块化程度高,包含了完整的路径规划流程和可视化展示,是学习和研究路径规划算法的优秀参考资料。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容






所有评论(0)