BP算法本质就是链式法则 利用计算图来理解BP算法
BP算法本质就是链式法则!
- 或者看成矩阵运算的嵌套
- 然后再来一个链式求导法则!
利用计算图来理解BP算法
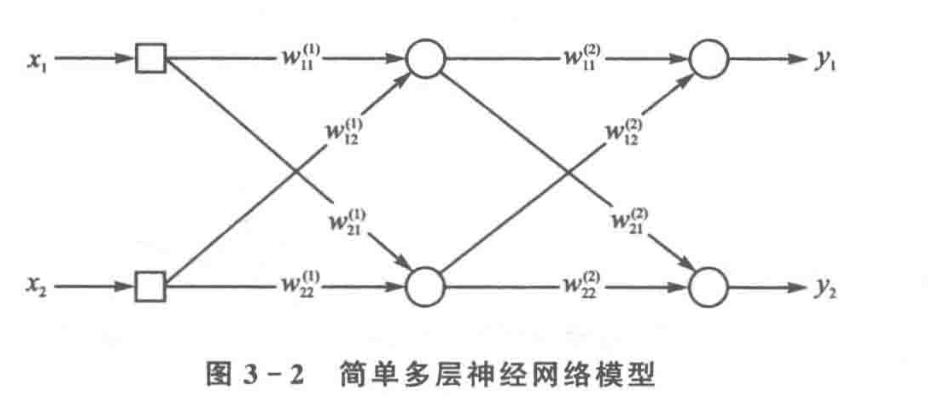
- 怎么将上面的图化成计算图呢?
- 那我就这样化简
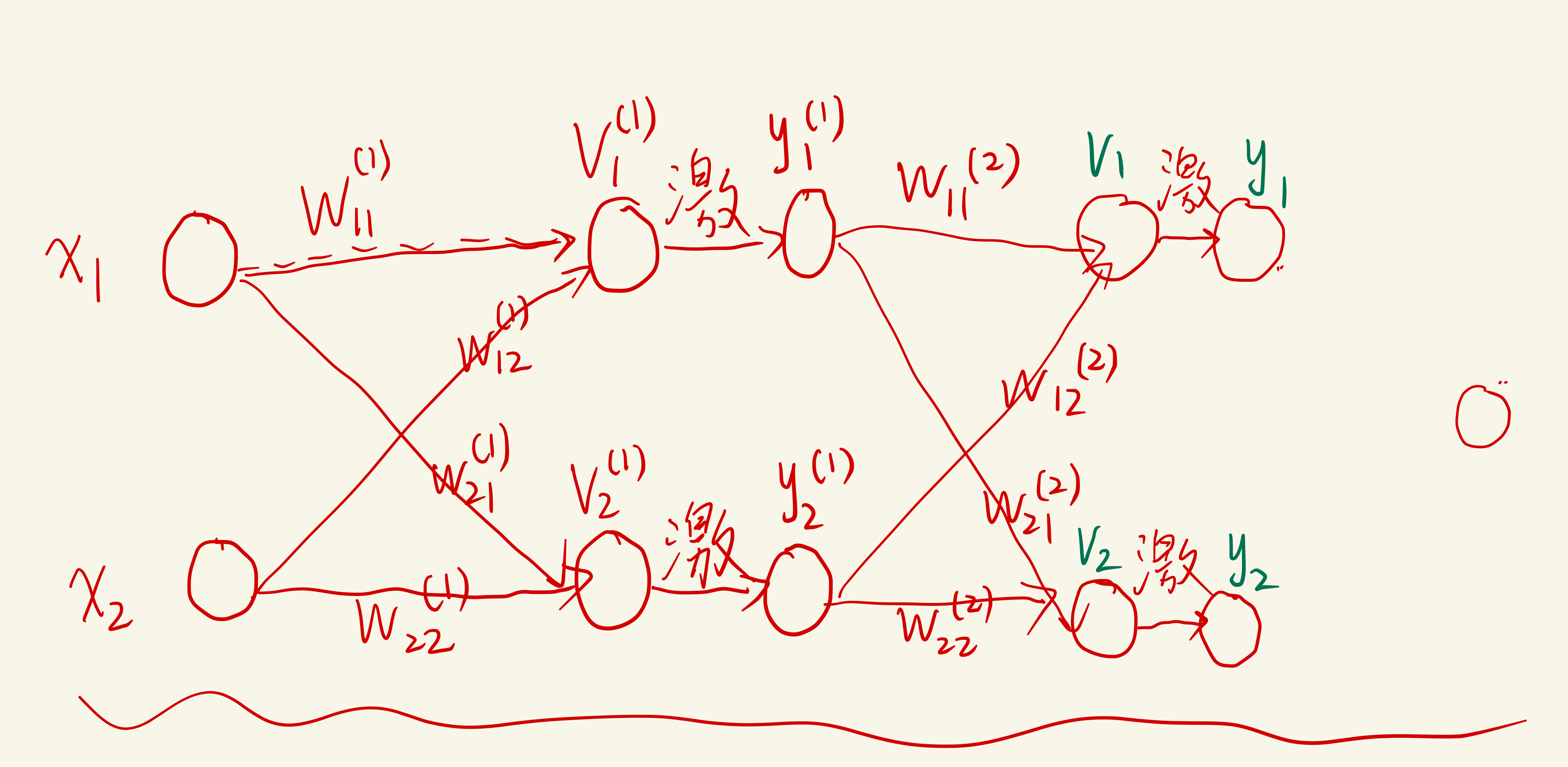
-
俺们肯定是想让L=12[(d1−y1)2+(d2−y2)2]L= \frac{1}{2}[(d_1 - y_1)^2 + (d_2 - y_2)^2]L=21[(d1−y1)2+(d2−y2)2]
-
最小啊!
-
下面就计算∂L∂各种参数啊\frac{\partial{L}}{\partial{各种参数啊}}∂各种参数啊∂L
-
∂Lw11(1)\frac{\partial{L}}{w_{11}^{(1)}}w11(1)∂L
∂L∂y1∂y1∂v1∂v1∂y1(1)∂y1(1)∂v1(1)x1+∂L∂y2∂y2∂v2∂v2∂y1(1)∂y1(1)∂v1(1)x1\frac{\partial{L}}{\partial{y_1}} \frac{\partial{y_1}}{\partial{v_1}}\frac{\partial{v_1}}{\partial{y_1^{(1)}}} \frac{\partial{y_1^{(1)}}}{\partial{v_1^{(1)}}}x_1+ \frac{\partial{L}}{\partial{y_2}}\frac{\partial{y_2}}{\partial{v_2}}\frac{\partial{v_2}}{\partial{y_1^{(1)}}}\frac{\partial{y_1^{(1)}}}{\partial{v_1^{(1)}}}x_1∂y1∂L∂v1∂y1∂y1(1)∂v1∂v1(1)∂y1(1)x1+∂y2∂L∂v2∂y2∂y1(1)∂v2∂v1(1)∂y1(1)x1
∂L∂y1∂y1∂v1w11(2)∂y1(1)∂v1(1)x1+∂L∂y2∂y2∂v2w21(2)∂y1(1)∂v1(1)x1\frac{\partial{L}}{\partial{y_1}} \frac{\partial{y_1}}{\partial{v_1}} w_{11}^{(2)} \frac{\partial{y_1^{(1)}}}{\partial{v_1^{(1)}}}x_1+ \frac{\partial{L}}{\partial{y_2}}\frac{\partial{y_2}}{\partial{v_2}}w_{21}^{(2)}\frac{\partial{y_1^{(1)}}}{\partial{v_1^{(1)}}}x_1∂y1∂L∂v1∂y1w11(2)∂v1(1)∂y1(1)x1+∂y2∂L∂v2∂y2w21(2)∂v1(1)∂y1(1)x1

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)