水下机器人双机械手系统动态建模与控制matlab仿真 水下机器人-机械手系统（Underwater vehicle-manipulator systems, UVMS）可以完成除观测之外的水下采样、抓取、操作等任务,在海洋科学考察、海洋工程等领域得到广泛应用。 通过对近年来国内外UVMS的研究现状进行综述,介绍了不同的UVMS本体结构与机械手构型,总结了UVMS的运动学、动力学和水动力学的建模方法,分析了人机交互式遥控操作控制方式,针对UVMS的自主控制中的运动规划、位置与轨迹跟踪、独立与协调控制、运动补偿控制、力/位置混合控制、视觉伺服控制等问题做了分类阐述。 该项目体现UVDMS（水下机器人双机械手系统）上的运动学、动力学和控制模拟器。 采用DH法建立运动学模型，并使用牛顿-欧拉法建立动力学模型。 该项目为UVDMS的水下抓取操作提供了一个演示。

在海洋探索的广阔领域中，水下机器人 - 机械手系统（UVMS）宛如深海中的多面手，除了常规的观测，还能高效完成采样、抓取和操作等复杂任务，广泛应用于海洋科学考察与海洋工程等关键领域。今天，咱们就深入探讨下其中的水下机器人双机械手系统（UVDMS）的动态建模与控制以及Matlab仿真实现。

UVDMS研究现状综述

近年来，UVMS在国内外的研究可谓热火朝天。不同的UVMS本体结构与机械手构型层出不穷，就像各具特色的深海舞者，各有千秋。同时，在建模与控制方面，运动学、动力学和水动力学的建模方法不断推陈出新，人机交互式遥控操作控制方式也备受关注。而在自主控制领域，从运动规划到位置与轨迹跟踪，从独立与协调控制到运动补偿控制，再到力/位置混合控制和视觉伺服控制等，每一个环节都充满了挑战与机遇，也成为了研究的热点。

UVDMS的建模

运动学模型：DH法的魅力

采用DH（Denavit - Hartenberg）法来建立UVDMS的运动学模型，这就像是为机器人的各个关节和连杆之间搭建起了一座沟通的桥梁，让我们能清晰地了解机械手在空间中的姿态与位置关系。以一个简单的2自由度机械手为例（实际UVDMS可能更复杂）：

% 定义连杆参数
L1 = 1; % 连杆1长度
L2 = 1; % 连杆2长度

% 关节变量
theta1 = pi/4; % 关节1角度
theta2 = pi/4; % 关节2角度

% DH参数矩阵
A1 = [cos(theta1), -sin(theta1), 0, L1*cos(theta1);
      sin(theta1), cos(theta1), 0, L1*sin(theta1);
      0, 0, 1, 0;
      0, 0, 0, 1];

A2 = [cos(theta2), -sin(theta2), 0, L2*cos(theta2);
      sin(theta2), cos(theta2), 0, L2*sin(theta2);
      0, 0, 1, 0;
      0, 0, 0, 1];

% 末端执行器相对于基坐标系的变换矩阵
T = A1*A2;

在这段代码中，我们首先定义了连杆的长度和关节的角度，然后依据DH法构建了每个连杆的变换矩阵A1和A2，最后通过矩阵相乘得到末端执行器相对于基坐标系的变换矩阵T，这个矩阵就准确描述了机械手末端在空间中的位置和姿态。

动力学模型：牛顿 - 欧拉法的力量

使用牛顿 - 欧拉法建立动力学模型，它就像给机器人注入了“力量”，让我们能深入分析机械手运动时所受力与力矩的变化。牛顿 - 欧拉法从力和力矩的平衡方程出发，逐步推导系统的动力学方程。这里涉及到复杂的力学分析和数学推导，虽然代码实现相对复杂，但却是理解机器人运动本质的关键。例如，在Matlab中实现牛顿 - 欧拉法计算关节力和力矩时，我们需要考虑各个连杆的质量、惯性张量以及速度、加速度等因素：

% 假设已经通过运动学模型得到了连杆的速度和加速度信息
% 定义连杆质量
m1 = 1;
m2 = 1;

% 定义连杆惯性张量
I1 = [1 0 0; 0 1 0; 0 0 1];
I2 = [1 0 0; 0 1 0; 0 0 1];

% 计算关节力和力矩（简化示例，实际需更复杂推导）
f1 = m1*a1 + cross(omega1, cross(omega1, r1)) +...
     m2*(a2 + cross(omega2, cross(omega2, r2)));
tau1 = I1*alpha1 + cross(omega1, I1*omega1) +...
       cross(r1, m1*a1) + cross(r2, m2*a2);

上述代码只是一个简化示例，实际中我们需要根据详细的运动学分析，精确计算每个连杆的速度omega、加速度alpha以及质心位置r等信息，进而准确计算出关节力f和力矩tau，为后续的控制奠定基础。

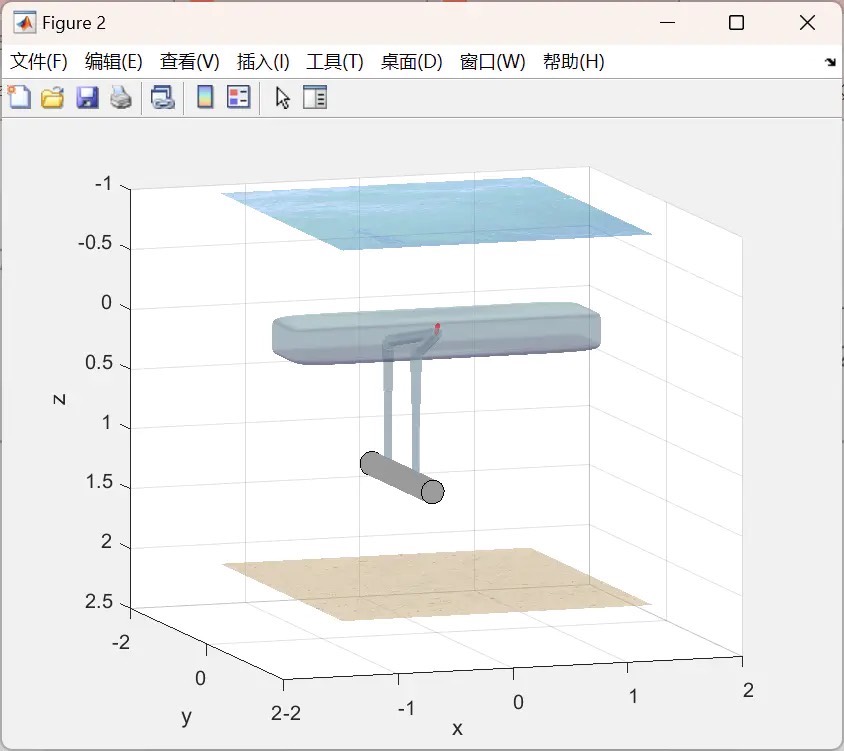
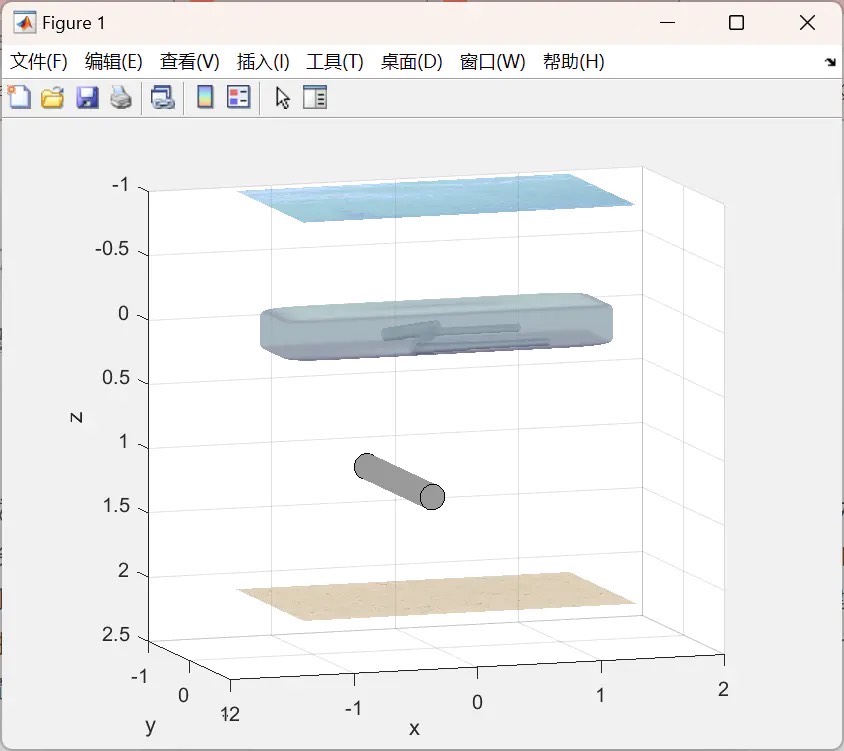
UVDMS的控制与Matlab仿真演示

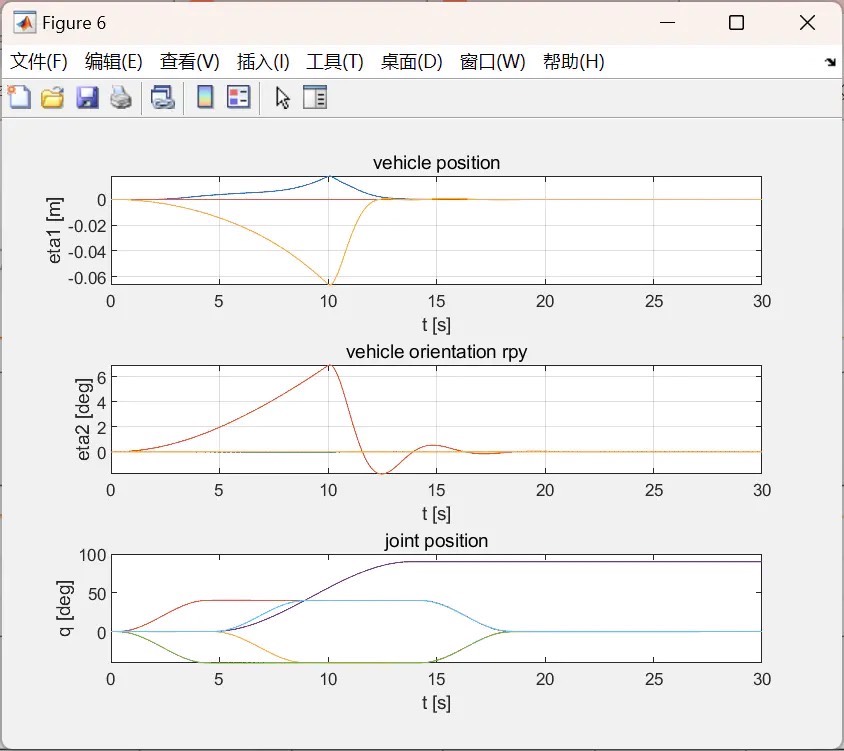
该项目不仅仅是建模，还为UVDMS的水下抓取操作提供了一个精彩的演示。通过Matlab强大的仿真功能，我们可以模拟UVDMS在水下的各种抓取场景。在控制方面，无论是运动规划算法确保机械手准确到达目标位置，还是位置与轨迹跟踪算法使机械手精确跟随预设轨迹，Matlab都提供了丰富的工具和函数库来实现。

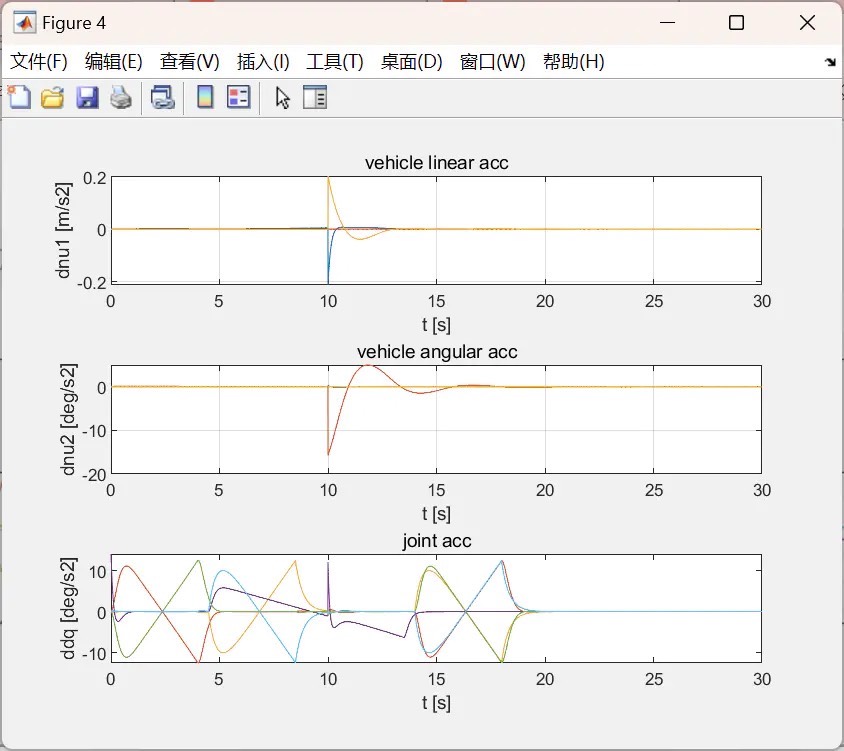
水下机器人双机械手系统动态建模与控制matlab仿真 水下机器人-机械手系统（Underwater vehicle-manipulator systems, UVMS）可以完成除观测之外的水下采样、抓取、操作等任务,在海洋科学考察、海洋工程等领域得到广泛应用。 通过对近年来国内外UVMS的研究现状进行综述,介绍了不同的UVMS本体结构与机械手构型,总结了UVMS的运动学、动力学和水动力学的建模方法,分析了人机交互式遥控操作控制方式,针对UVMS的自主控制中的运动规划、位置与轨迹跟踪、独立与协调控制、运动补偿控制、力/位置混合控制、视觉伺服控制等问题做了分类阐述。 该项目体现UVDMS（水下机器人双机械手系统）上的运动学、动力学和控制模拟器。 采用DH法建立运动学模型，并使用牛顿-欧拉法建立动力学模型。 该项目为UVDMS的水下抓取操作提供了一个演示。

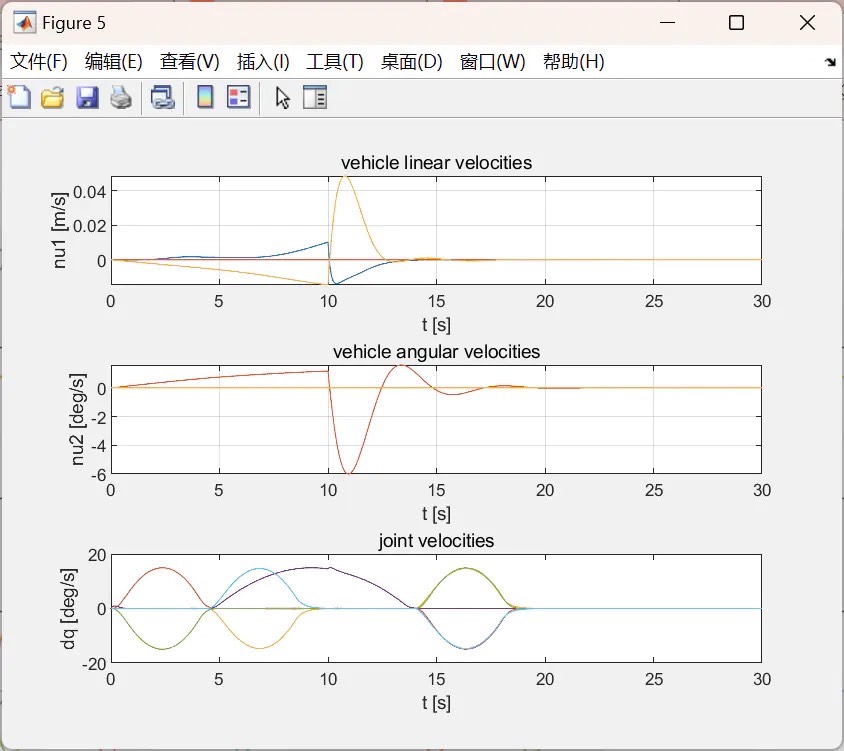
例如，在位置跟踪控制中，我们可以采用PID控制算法：

% 定义PID参数
Kp = 10;
Ki = 1;
Kd = 0.1;

% 设定目标位置
target_position = [1; 1];

% 初始化误差和积分项
error = 0;
integral = 0;
prev_error = 0;

for i = 1:100 % 模拟时间步
    % 获取当前位置（假设已有获取位置的函数）
    current_position = get_current_position();
    
    % 计算误差
    error = target_position - current_position;
    
    % 计算积分项
    integral = integral + error;
    
    % 计算微分项
    derivative = error - prev_error;
    
    % 计算控制量
    control_signal = Kp*error + Ki*integral + Kd*derivative;
    
    % 执行控制（假设已有执行控制的函数）
    execute_control(control_signal);
    
    % 更新上一时刻误差
    prev_error = error;
end

这段代码展示了PID控制算法在Matlab中的基本实现，通过不断调整比例（Kp）、积分（Ki）和微分（Kd）系数，使机械手尽可能准确地跟踪目标位置。在实际的UVDMS仿真中，结合前面建立的运动学和动力学模型，就能实现更加真实、高效的水下抓取操作模拟。

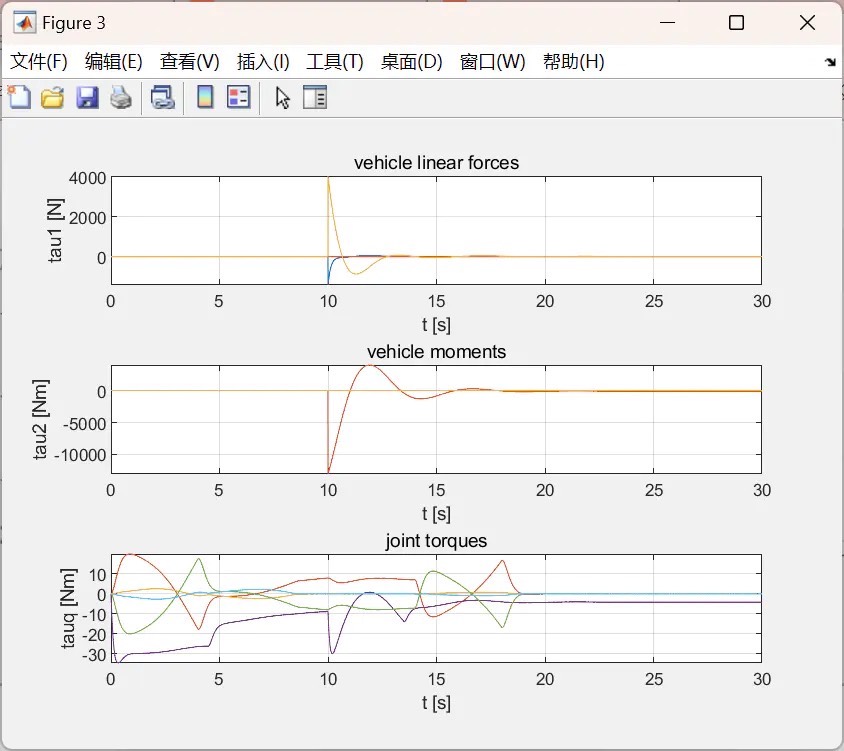
水下机器人双机械手系统的动态建模与控制是一个充满挑战与创新的领域，Matlab作为强大的工具，为我们探索这个领域提供了有力的支持。希望通过以上的介绍，能让大家对UVDMS的Matlab仿真有更深入的理解，也期待更多的探索和突破在这片海洋科技的蓝海中涌现。