机械臂运动仿真，机器人工具箱，matlab。 机器人示教，工作空间，正逆运动学。 轨迹画图，运动信息分析。

在机器人领域，机械臂的运动仿真是一项关键的研究内容，它能帮助我们在实际制造与部署前，深入了解机械臂的性能与行为。今天，就来聊聊借助Matlab和机器人工具箱，实现机械臂运动仿真相关的那些事儿，包括机器人示教、工作空间分析、正逆运动学计算，还有轨迹画图与运动信息分析。

机器人工具箱与Matlab的强强联合

Matlab作为强大的数学计算与编程平台，搭配机器人工具箱，为机械臂运动仿真提供了绝佳环境。机器人工具箱里包含了众多预定义的函数和模型，大大简化了开发流程。比如，要创建一个简单的2自由度平面机械臂模型，可以这样写代码：

% 创建2自由度平面机械臂
L(1) = Link('d', 0, 'a', 1, 'alpha', 0);
L(2) = Link('d', 0, 'a', 1, 'alpha', 0);
robot = SerialLink(L, 'name', '2DOF Planar Robot');

在这段代码中，Link函数用于定义每个关节的参数，d表示关节偏移，a是连杆长度，alpha为扭转角。通过将这些Link组合成SerialLink对象，就构建出了我们的机械臂模型。

机器人示教与工作空间

机器人示教是确定机械臂如何在空间中移动以完成任务的过程。而工作空间则定义了机械臂末端执行器能够到达的空间范围。

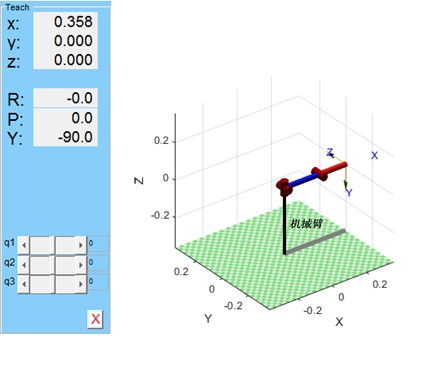
计算机械臂的工作空间，可以使用机器人工具箱中的workspace函数。

% 计算并绘制工作空间
ws = robot.workspace('n', 1000);
figure;
plot3(ws(:,1), ws(:,2), ws(:,3), '.');
xlabel('X (m)');
ylabel('Y (m)');
zlabel('Z (m)');
title('2DOF Planar Robot Workspace');

上述代码先通过workspace函数计算工作空间，参数'n'指定了采样点数。然后利用plot3函数将工作空间在三维坐标系中绘制出来，这样就能直观看到机械臂的可达范围。

正逆运动学

正运动学是根据关节角度计算末端执行器位置和姿态的过程，逆运动学则相反，是根据期望的末端位置和姿态求解关节角度。

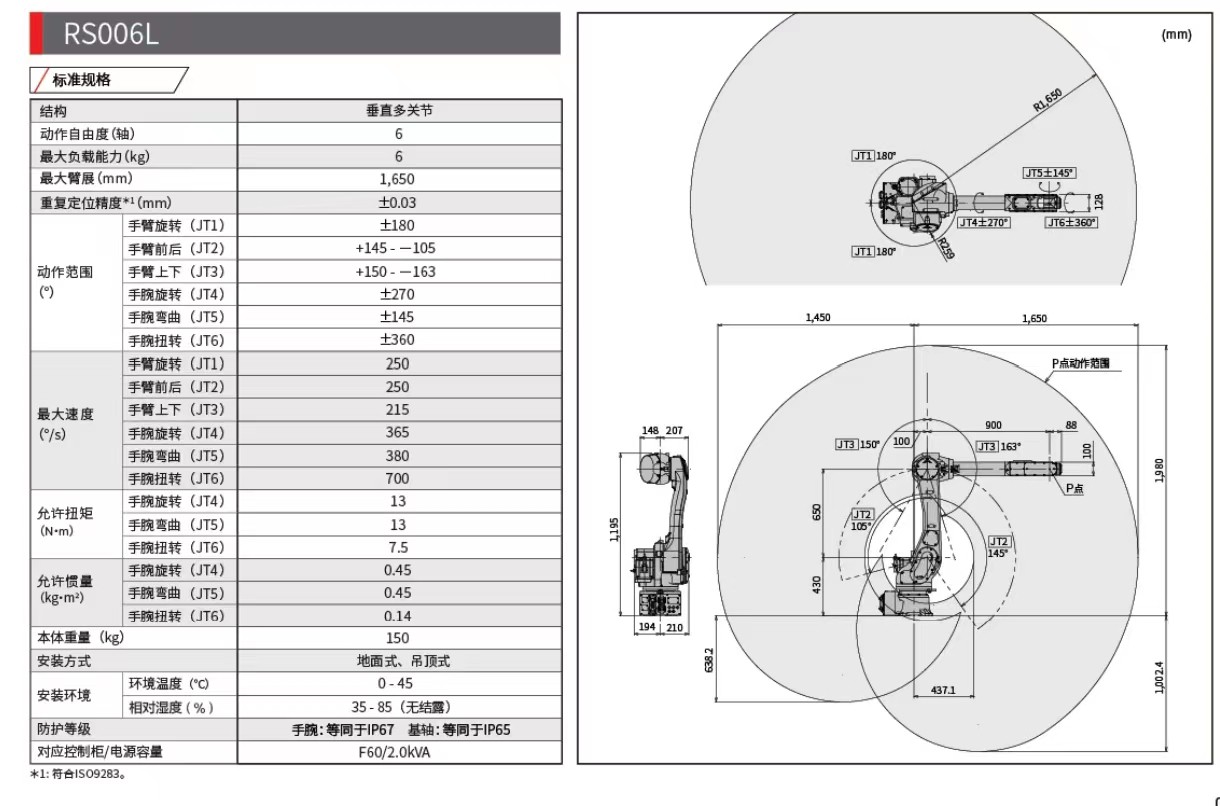
在机器人工具箱里，正运动学计算非常简单：

% 正运动学示例
q = [pi/4 pi/4]; % 设定关节角度
T = robot.fkine(q); % 计算末端执行器位姿
disp(T);

这里设置了两个关节角度q，通过fkine函数计算出末端执行器的位姿矩阵T并显示。

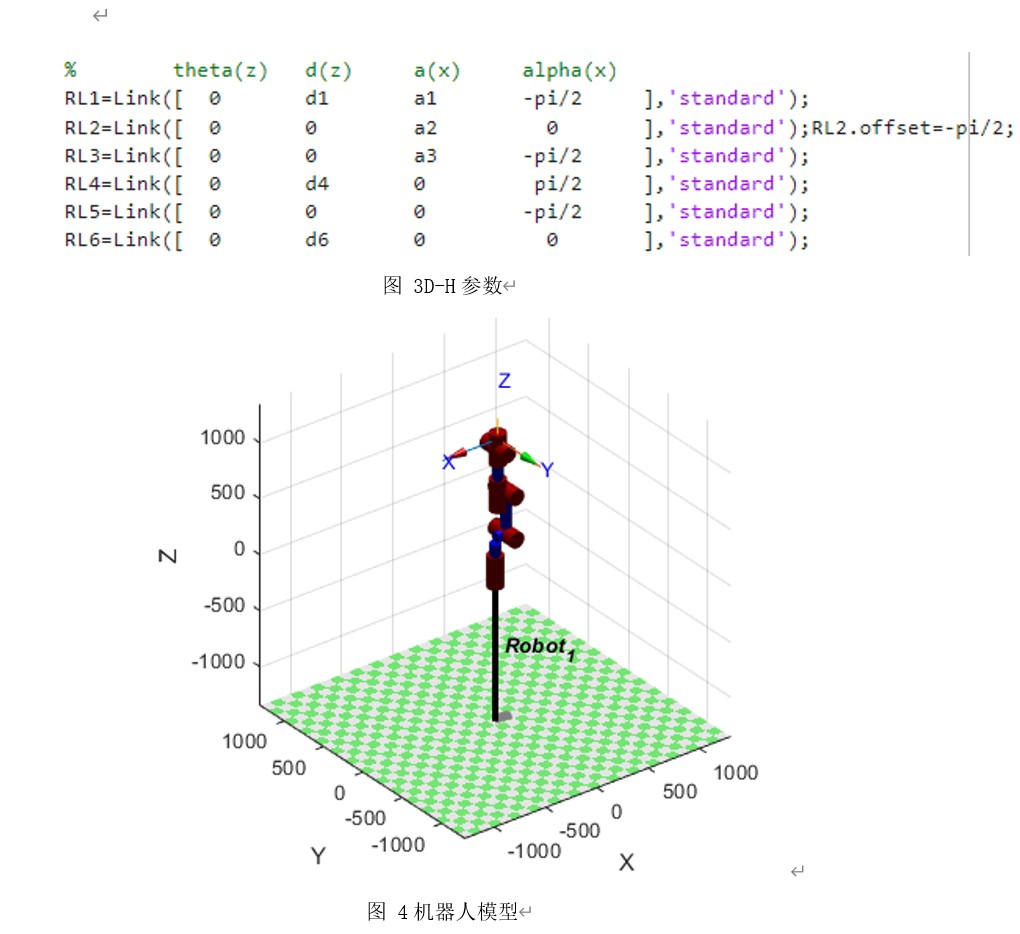
机械臂运动仿真，机器人工具箱，matlab。 机器人示教，工作空间，正逆运动学。 轨迹画图，运动信息分析。

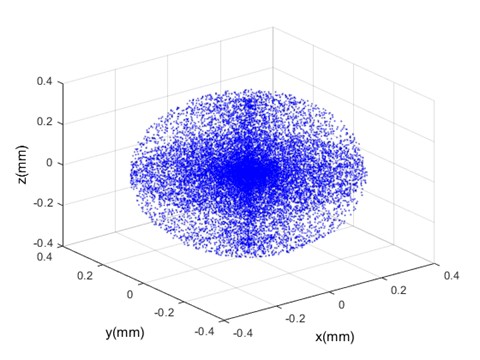
逆运动学相对复杂一些，因为可能存在多组解。以求解到达特定位置的关节角度为例：

% 逆运动学示例
x = 1.5; y = 1; z = 0; % 期望的末端位置
T0 = transl(x, y, z); % 创建期望的位姿矩阵
q_sol = robot.ikine(T0); % 求解逆运动学
disp(q_sol);

transl函数创建了期望的位姿矩阵T0，ikine函数尝试求解出能使机械臂末端到达该位置的关节角度q_sol。

轨迹画图与运动信息分析

轨迹画图能直观展示机械臂的运动路径，运动信息分析则帮助我们了解速度、加速度等关键参数。

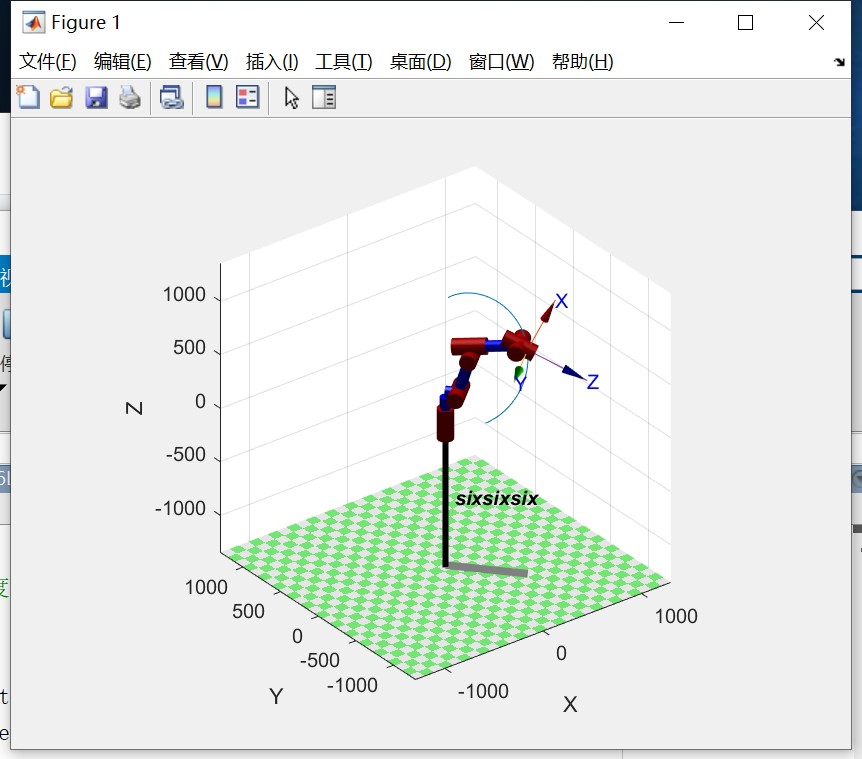
假设要让机械臂沿着一条直线轨迹运动，可以这样实现：

% 直线轨迹规划与绘制
x_start = 0; y_start = 0; z_start = 0;
x_end = 2; y_end = 2; z_end = 0;
t = 0:0.1:1; % 时间向量
x = interp1([0 1], [x_start x_end], t);
y = interp1([0 1], [y_start y_end], t);
z = interp1([0 1], [z_start z_end], t);
figure;
hold on;
for i = 1:length(t)
    T = transl(x(i), y(i), z(i));
    q = robot.ikine(T);
    robot.plot(q);
    drawnow;
end
hold off;

这段代码首先定义了直线轨迹的起点和终点，通过interp1函数在时间向量t上进行线性插值得到各个时刻的位置。然后在循环中，根据每个位置求解逆运动学得到关节角度，并使用plot函数绘制机械臂在该时刻的形态，从而形成动态的轨迹展示。

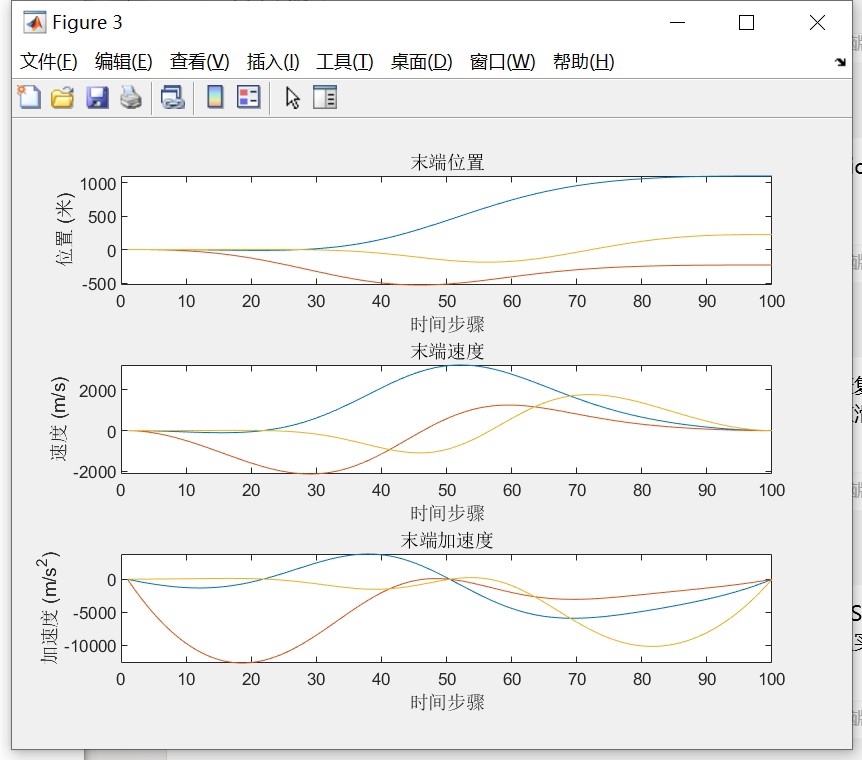
要分析运动信息，比如关节速度，可以在轨迹规划的基础上添加如下代码：

% 关节速度分析
q_dot = zeros(size(q));
for i = 2:length(t)
    q_dot(:,i) = (q(:,i) - q(:,i - 1)) / (t(i) - t(i - 1));
end
figure;
for j = 1:robot.n
    subplot(robot.n, 1, j);
    plot(t(2:end), q_dot(j, 2:end));
    title(['Joint ', num2str(j),'Velocity']);
    xlabel('Time (s)');
    ylabel('Velocity (rad/s)');
end

这里通过前后时刻关节角度的差值除以时间间隔，计算出关节速度q_dot，并绘制出每个关节速度随时间变化的曲线，方便我们分析机械臂运动过程中的速度特性。

通过Matlab和机器人工具箱，我们可以全面深入地对机械臂运动进行仿真、分析，为实际机器人的设计与控制提供有力支持。希望这篇博文能给对机械臂运动仿真感兴趣的小伙伴们一些启发！