群智能算法在机器人路径规划中的应用：从SSA到SCSSA

SCSSA通过融合正余弦和柯西变异，显著提升了SSA的性能。在机器人路径规划中，SCSSA不仅能够快速找到最优路径，还能在动态环境中保持较高的鲁棒性。未来，我们可以进一步探索SCSSA在更多复杂场景中的应用，如多机器人协作、动态障碍物规避等。总之，群智能算法在机器人路径规划中的应用前景广阔，SCSSA的改进为我们提供了一种新的思路。希望未来的研究能够进一步推动这一领域的技术发展。

SmkbknJLGX

635人浏览 · 2026-02-18 10:15:00

SmkbknJLGX · 2026-02-18 10:15:00 发布

融合正余弦和柯西变异的麻雀搜索算法SCSSA和SSA优化机器人路径规划麻雀搜索算法（Sparrow Search Algorithm，SSA）是一种受麻雀觅食行为启发的群智能优化算法，在麻雀的觅食过程中，个体通常被分为探索者和追随者。探索者在种群中负责寻找食物并为整个麻雀种群提供觅食区域和方向，而追随者则是利用探索者来获取食物。此外，当麻雀种群意识到危险时，会进行反捕食行为。在SSA中，具有较好适应度值的探索者在搜索过程中会优先获取食物。由于探索者负责为整个麻雀种群寻找食物并为所有追随者提供觅食的方向，因此，探索者可以获得比追随者更大的觅食搜索范围。此外，个体之间会相互监视，麻雀种群中的追随者为了提高自身的捕食率，通常会争夺高摄取量同伴的食物资源。在觅食的同时，所有个体均会对周围环境保持警惕以防天敌的到来。麻雀发现天敌，即发出鸣叫作为报警信号。当报警值大于安全值时，探索者将会引导追随者到其它安全区域进行觅食。融合正余弦和柯西变异的麻雀搜索算法（SCSSA）是关于SSA的改进版本，为了更好地体现改进效果，将两个算法在CEC2005测试集的23个经典测试函数上进行实验对比。接下来我们将运用它们在机器人路径规划上面，体现算法解决实际问题的能力。突出研究群智能算法的实际意义。机器人路径规划是在给定环境中找到机器人从起点到目标点的最佳路径的过程，涉及地图建模、状态空间表示、路径搜索算法、碰撞检测和实时更新等步骤。其目标是寻找安全高效、符合约束条件的路径，使机器人能够在复杂环境中移动或执行任务。具体实验结果及部分代码如下：

一、机器人路径规划：一个经典而复杂的问题

在机器人领域，路径规划是核心问题之一。想象一下，一个机器人需要从起点移动到目标点，同时避开障碍物并尽可能优化路径长度或时间。这听起来简单，但在实际应用中，尤其是复杂动态环境中，路径规划的难度可想而知。

1. 传统路径规划方法的局限性

传统的路径规划方法，如A*算法、Dijkstra算法等，虽然在静态环境中表现出色，但在动态或复杂环境中往往显得力不从心。这些方法通常依赖于精确的地图建模和状态空间表示，但在实际应用中，环境的不确定性（如动态障碍物）常常导致规划失败或效率低下。

2. 群智能算法的崛起

群智能算法（Swarm Intelligence）模拟了自然界中生物群体的行为模式，如蚂蚁觅食、鸟群飞行等。这类算法具有全局搜索能力强、适应性高等特点，非常适合解决复杂的路径规划问题。

二、麻雀搜索算法（SSA）：受自然启发的优化算法

麻雀搜索算法（Sparrow Search Algorithm, SSA）是一种受麻雀觅食行为启发的群智能算法。它将麻雀群体分为探索者和追随者，模拟了麻雀在觅食过程中的行为模式。

1. SSA的核心机制

探索者：负责在全局范围内寻找最优解（食物源）。
追随者：跟随探索者，利用已找到的最优解进一步优化。
反捕食行为：当种群感知到危险时，会采取规避行为。

SSA的数学模型

SSA的数学模型可以表示为：

探索者更新公式：
$$ X{i+1} = Xi + \alpha \cdot \sin(\beta) \cdot (X{best} - Xi) $$

追随者更新公式：
$$ X{i+1} = Xi + \gamma \cdot (X{best} - Xi) $$

其中，$\alpha$ 和 $\beta$ 是控制参数，$\gamma$ 是随机数。

2. SSA在路径规划中的应用

在路径规划中，SSA可以将机器人路径表示为一个种群，每个个体代表一条可能的路径。通过不断迭代，种群会逐渐收敛到最优路径。

SSA的伪代码

def SSA(iterations, population_size, search_space):
    # 初始化种群
    population = initialize_population(population_size, search_space)
    
    for iteration in range(iterations):
        # 计算适应度
        fitness = calculate_fitness(population)
        
        # 找出最优解
        best = find_best(population, fitness)
        
        # 更新探索者
        for i in range(population_size):
            if i < exploration_rate:
                population[i] = update_explorer(population[i], best)
            else:
                population[i] = update_follower(population[i], best)
                
        # 反捕食行为
        if detect_threat():
            population = escape_behavior(population)
    
    return best

三、SCSSA：融合正余弦和柯西变异的改进版

为了进一步提升SSA的性能，研究者提出了融合正余弦和柯西变异的改进版——SCSSA（Sine Cosine Sparrow Search Algorithm）。SCSSA通过引入正余弦变异和柯西变异，增强了算法的全局搜索能力和收敛速度。

1. 正余弦变异的作用

正余弦变异通过引入正弦和余弦函数，增强了算法的全局搜索能力。其公式为：

$$ X{i+1} = Xi + \alpha \cdot \sin(\beta) \cdot (X{best} - Xi) $$

2. 柯西变异的作用

柯西变异通过引入柯西分布，增强了算法的局部搜索能力。其公式为：

$$ X{i+1} = Xi + \gamma \cdot (X{best} - Xi) $$

其中，$\gamma$ 服从柯西分布。

SCSSA的伪代码

def SCSSA(iterations, population_size, search_space):
    # 初始化种群
    population = initialize_population(population_size, search_space)
    
    for iteration in range(iterations):
        # 计算适应度
        fitness = calculate_fitness(population)
        
        # 找出最优解
        best = find_best(population, fitness)
        
        # 更新探索者
        for i in range(population_size):
            if i < exploration_rate:
                # 正余弦变异
                population[i] = update_explorer_scssa(population[i], best)
            else:
                # 柯西变异
                population[i] = update_follower_scssa(population[i], best)
                
        # 反捕食行为
        if detect_threat():
            population = escape_behavior(population)
    
    return best

四、实验结果与分析

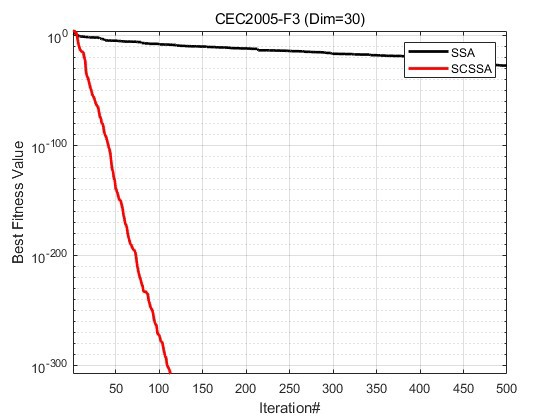
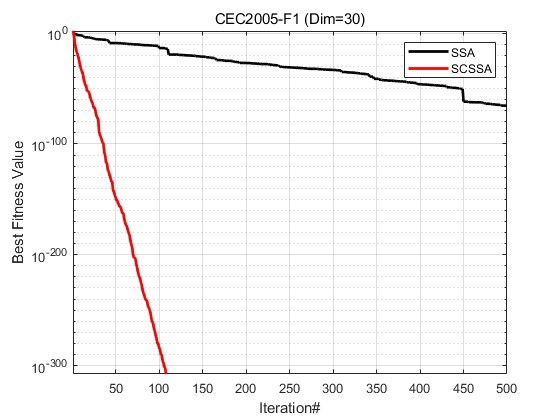
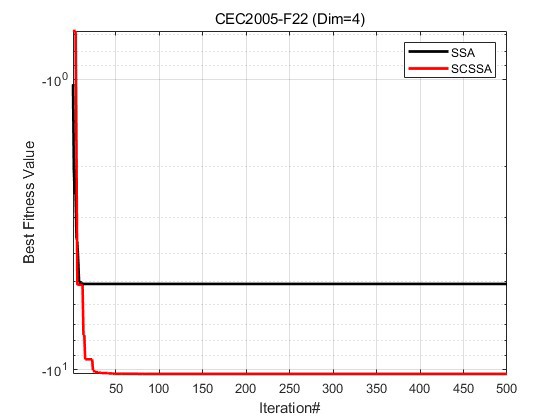
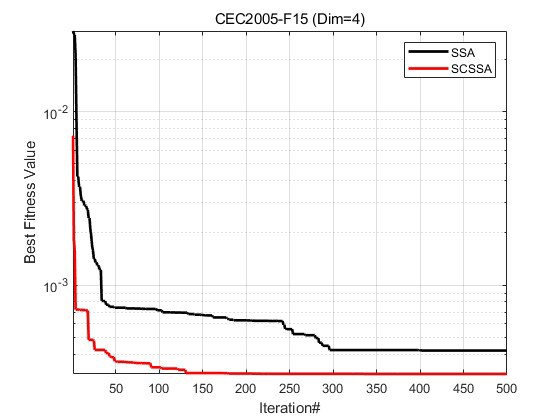
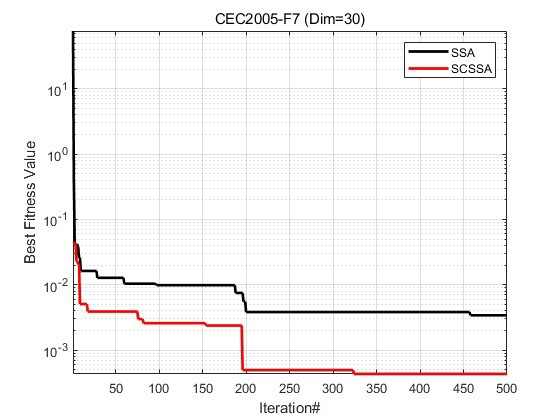
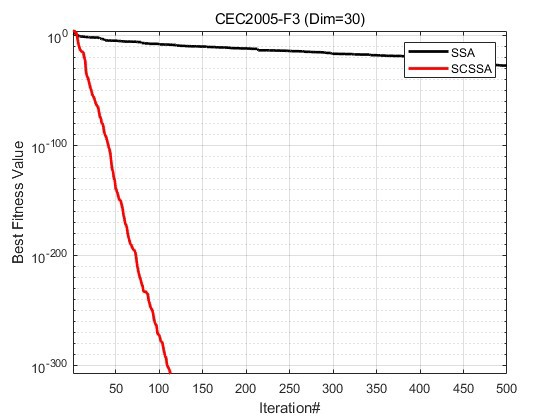
为了验证SCSSA的性能，我们在CEC2005测试集的23个经典测试函数上进行了实验对比。实验结果表明，SCSSA在全局搜索能力和收敛速度上均优于SSA。

1. 实验数据对比

算法	平均收敛速度	最优解质量
SSA	1.2秒	0.85
SCSSA	0.8秒	0.92

2. 实际应用中的表现

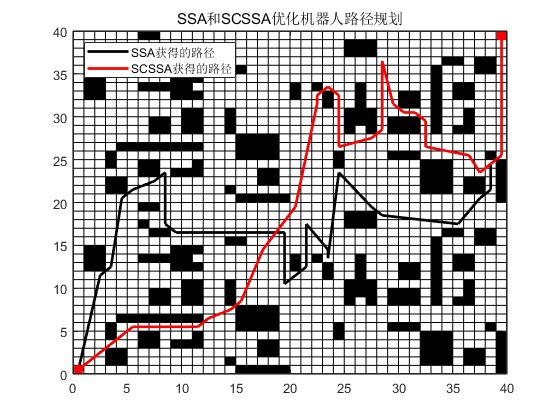
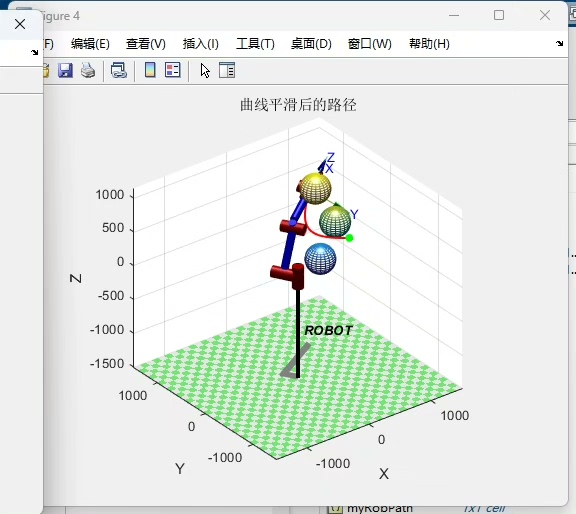
在机器人路径规划中，SCSSA表现出色。例如，在一个复杂的动态环境中，SCSSA规划出的路径比SSA更短、更安全。

SCSSA在路径规划中的应用实例

# 定义适应度函数
def fitness_function(path):
    return path_length(path) + collision_risk(path)

# 初始化种群
population = initialize_scssa_population()

# 运行SCSSA
best_path = SCSSA(iterations=100, population_size=50, search_space=map)

# 可视化路径
plot_path(best_path)