MATLAB并联机器人Stewart平台pid控制仿真simulink simscape 运动学 动力学

在机器人领域，并联机器人以其独特的结构和优势备受关注，Stewart平台就是其中的典型代表。今天咱就唠唠在MATLAB环境下，如何对Stewart平台开展从运动学、动力学到PID控制仿真的一系列操作，还会用到Simulink和Simscape这些超好用的工具。

一、Stewart平台运动学

Stewart平台由上下两个平台通过六根可伸缩杆连接而成。要对其进行控制，首先得搞清楚运动学关系，也就是已知各伸缩杆的长度，如何求解平台的位姿（位置和姿态），这叫逆运动学；反之，已知平台位姿求各伸缩杆长度，就是正运动学。

以逆运动学为例，假设Stewart平台上下平台的几何参数已知，通过建立坐标系，利用向量关系和几何约束，可以推导出逆运动学方程。在MATLAB里，代码实现大概像这样：

% 定义Stewart平台几何参数
upper_radius = 0.2;
lower_radius = 0.3;
platform_height = 0.5;

% 已知平台位姿（示例）
x = 0.1;
y = 0.1;
z = 0.6;
roll = 0;
pitch = 0;
yaw = 0;

% 计算逆运动学
T = eul2tform([roll,pitch,yaw],'ZYX');
T(1,4) = x;
T(2,4) = y;
T(3,4) = z;

upper_points = [upper_radius*[cos(0:60:300);sin(0:60:300)];ones(1,6)];
lower_points = [lower_radius*[cos(0:60:300);sin(0:60:300)];zeros(1,6)];

upper_points_transformed = T * upper_points;

lengths = zeros(1,6);
for i = 1:6
    lengths(i) = norm(upper_points_transformed(:,i) - lower_points(:,i));
end
disp(lengths);

这段代码首先定义了Stewart平台上下平台的半径以及平台高度等几何参数。接着设定了平台的一个示例位姿（包括位置和姿态）。通过欧拉角转齐次变换矩阵得到平台的位姿变换矩阵T ，对平台上表面的点进行变换。最后通过计算上下对应点之间的距离，得到六根伸缩杆的长度。

二、Stewart平台动力学

动力学研究的是力与运动之间的关系，对于Stewart平台来说，就是要分析施加在伸缩杆上的力如何影响平台的运动。一般基于拉格朗日方程来建立动力学模型。拉格朗日函数定义为系统动能减去势能，通过对拉格朗日函数求导可以得到系统的动力学方程。

在MATLAB中，虽然直接手推动力学方程并编程实现较为复杂，但借助符号运算工具箱可以简化这个过程。

syms x y z roll pitch yaw real
syms q1 q2 q3 q4 q5 q6 real
syms u1 u2 u3 u4 u5 u6 real

% 定义几何参数
a = 0.2;
b = 0.3;
h = 0.5;

% 运动学关系推导（这里简化，实际更复杂）
% ......

% 动能和势能计算
% ......

L = kinetic_energy - potential_energy;
eqns = eulerLagrange(L, [q1,q2,q3,q4,q5,q6], [u1,u2,u3,u4,u5,u6]);

这段代码先定义了符号变量，包括平台的位姿变量、伸缩杆长度变量以及输入力变量。接着设定几何参数，之后就是通过符号运算来推导运动学关系，计算动能和势能，进而构建拉格朗日函数L ，最后通过eulerLagrange函数得到系统的动力学方程eqns。

三、基于Simulink和Simscape的PID控制仿真

有了运动学和动力学基础，就可以进行控制仿真了。Simulink是MATLAB里强大的动态系统建模和仿真工具，Simscape则为多领域物理系统建模提供了便利。

MATLAB并联机器人Stewart平台pid控制仿真simulink simscape 运动学 动力学

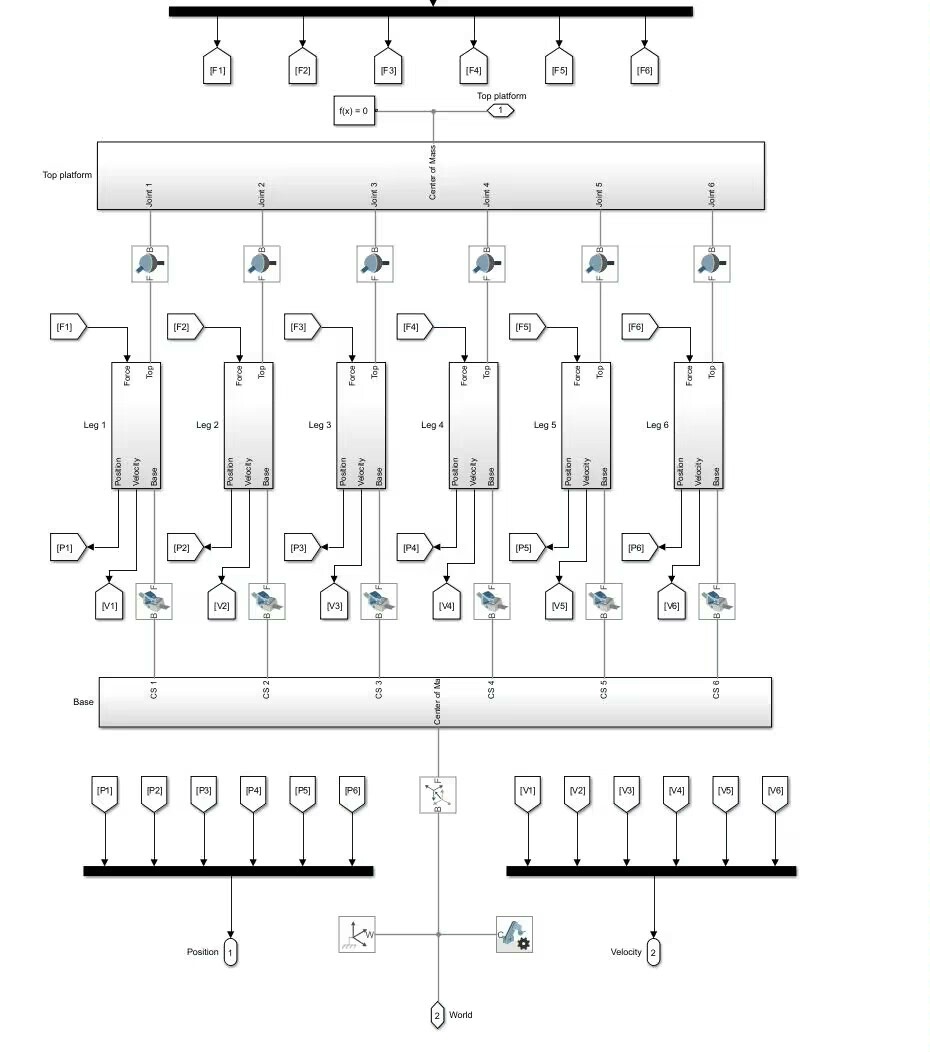
首先在Simulink里搭建Stewart平台的模型框架，利用Simscape中的机械库来构建平台的物理结构。将前面推导的运动学和动力学关系通过MATLAB Function模块嵌入到模型中。

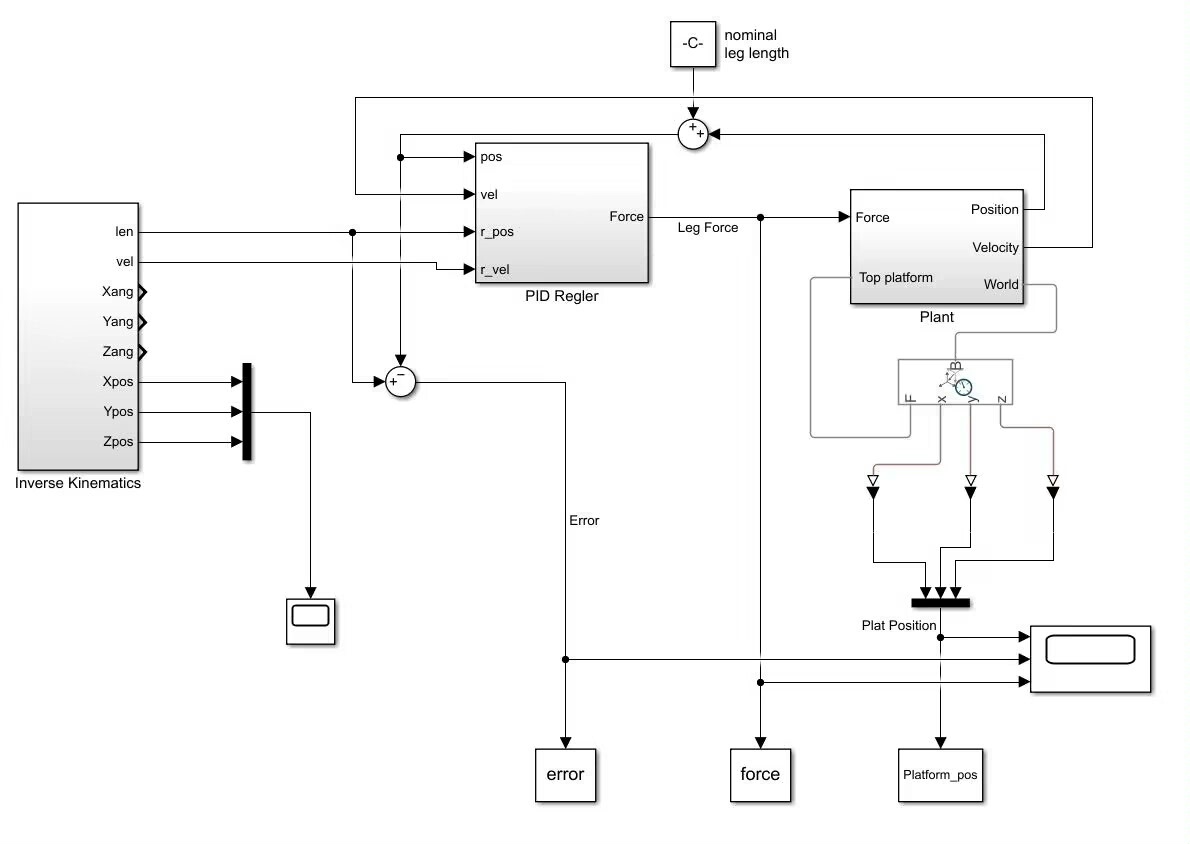
对于PID控制，PID控制器的作用是根据平台实际位姿与期望位姿的误差，调整伸缩杆的输入力，使平台尽可能接近期望位姿。在Simulink里，PID控制器可以直接从控制模块库中拖入。

% PID参数设定示例
Kp = 10;
Ki = 0.1;
Kd = 1;

% 误差计算
error = desired_pose - current_pose;

% PID控制律
control_signal = Kp*error + Ki*cumsum(error) + Kd*d(error);

这里简单设定了PID的比例、积分、微分系数Kp 、Ki 、Kd 。通过计算期望位姿与当前位姿的误差error，依据PID控制律计算出控制信号control_signal，这个信号最终会作用到Stewart平台的伸缩杆上，实现对平台位姿的控制。

在整个仿真过程中，通过不断调整PID参数以及观察平台的运动响应，可以优化控制效果，让Stewart平台更精准地跟踪期望轨迹。

通过在MATLAB中对Stewart平台进行运动学、动力学分析以及PID控制仿真，我们能够深入了解并联机器人的工作原理，并且为实际应用中的控制策略优化提供有力的支持。无论是搞科研还是做工程实践，这些知识和技能都相当实用。