【移动机器人运动规划】5 基于优化的轨迹规划 Part2

基于优化的轨迹规划方法综述本文系统介绍了基于优化的轨迹规划方法，重点对比了全局方法与局部方法的核心特点和应用场景。全局方法（如PRM*/RRT*）通过探索与利用寻找全局最优解，适合复杂环境；局部方法（如CHOMP/DDP）通过确定性优化追求局部最优，更适用于动力学约束场景。文章详细阐述了轨迹的定义与平滑性要求，并深入探讨了微分平坦理论在多旋翼系统中的应用优势。研究表明，在实际部署中采用前端（全局

YunchengLi

49人浏览 · 2026-02-13 17:53:16

YunchengLi · 2026-02-13 17:53:16 发布

5 基于优化的轨迹规划

文章目录

5 基于优化的轨迹规划
- 5.5 约束情形 Constrained case
- - 5.5.1 凸优化简化 Convex Simplification
  - 5.5.2 空间-时间变形轨迹优化方法 Spatial-Temporal Deformation

5.5 约束情形 Constrained case

受约束的轨迹优化：在满足各种物理、安全和动力学限制的前提下，寻找一条“最优”的运动路径。
优化数学形式
$\begin{aligned} & \min_{z(t),\, T} \quad \int_0^T v(t)^\top \mathbf{W} v(t)\, dt + \rho(T), \\ \text{s.t.}& \\ & \quad z^{(s)}(t) = v(t), \quad \forall t \in [0, T], \\ & \quad \mathcal{G}\big(z(t), \dot{z}(t), \dots, z^{(s)}(t)\big) \leq \mathbf{0}, \quad \forall t \in [0, T], \\ & \quad z(t) \in \mathcal{F}, \quad \forall t \in [0, T], \\ & \quad z^{[s-1]}(0) = \bar{z}_o, \quad z^{[s-1]}(T) = \bar{z}_f, \\ \text{where} &\quad z^{[s-1]} := \begin{bmatrix} z^\top & \dot{z}^\top & \ddot{z}^\top & \cdots & z^{(s-1)\top} \end{bmatrix}^\top. \end{aligned}$
四大难点
- 最优参数化形式未知
- 时-空剖面涉及很多自由度
- 动态可行性可能非凸
- 安全区域带来高复杂性

简化策略

简化方式	具体做法	优点	缺点
固定参数化	使用多项式样条（如5次、7次）	数学清晰，易求解	无法自适应最优时间
固定时间分配	假设每段飞行时间已知	降低变量数量	不能优化时间效率
简化动态可行性	用范数约束代替精确模型，如 $	a(t)	\leq a_\max$
局部凸化安全约束	将障碍物视为局部凸区域如：使用安全距离函数	可在线优化	仅适用于简单环境

5.5.1 凸优化简化 Convex Simplification

凸优化建模 Convex formulation
- 受线性约束的二次目标
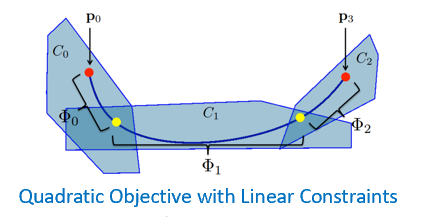
  - 轨迹被划分为多个多项式段（如 $C_0,C_1,C_2$ ）
  - 每个段由一个多项式函数 $\Phi_i(t)$ 描述
  - 安全区域用“飞行走廊”（safe flight corridors）表示，确保轨迹始终在安全范围内
- 数学模型
  $\begin{aligned} \arg\min_{\Phi} &\quad J^q = \sum_{i=0}^{n-1} \int_0^{\Delta t_i} \|\Phi_i^{(q)}(t)\|^2 dt \\ \text{s.t.} &\quad \Phi_i^{(k)}(\Delta t_i) = \Phi_{i+1}^{(k)}(0), \quad k = 0,\dots,q, \quad i = 1,\dots,N-2 \\ & \quad \Phi_0^{(k)}(0) = u_s^{(k)}, \quad \Phi_{N-1}^{(k)}(\Delta t_{N-1}) = u_y^{(k)}, \quad k = 0,\dots,q \\ & \quad \underbrace{\mathbf{A}_i^T \Phi_i(t) \leq \mathbf{b}_i,}_{安全约束} \quad i = 0,\dots,N-1 \end{aligned}$
- 目标：最小化第 $q$ 阶导数的平方积分，如 $q = 3$ → 最小化 jerk
- 约束
  - 边界条件：起始和终止状态
  - 连续性约束：相邻段之间各阶导数匹配
  - 线性不等式约束：保证轨迹在安全区域内（如障碍物避免）
- 这是一个 二次目标 + 线性约束 的优化问题 → 可转化为 QP（Quadratic Programming）！
代价函数：单段多项式的代价函数推导
- 假设多项式为 $f(t)=\sum_ip_it^i$ ，想最小化 4 阶导数的平方积分，即 snap
- 四阶导数
  $f^{(4)}(t) = \sum_{i\geq4} i(i-1)(i-2)(i-3)t^{i-4}p_i$
- 平方后积分
  $\begin{aligned} (f^{(4)}(t))^2 &= \sum_{i,j\geq4} i(i-1)(i-2)(i-3)j(j-1)(j-2)(j-3)t^{i+j-8}p_i p_j \\ J(T) &= \int_{T_{j-1}}^{T_j} (f^{(4)}(t))^2 dt \\ &= \sum_{i,j\geq4} \frac{i(i-1)(i-2)(i-3)j(j-1)(j-2)(j-3)}{i+j-7} (T_j^{i+j-7} - T_{j-1}^{i+j-7}) p_i p_j \\ \end{aligned}$
- 最终的代价函数
  $\Rightarrow J_j(T) = \mathbf{p}_j^\top \mathbf{Q}_j \mathbf{p}_j$
  每段的代价是系数向量 $\mathbf{p}_j$ 的二次型
等式约束
- 单段边界条件：如何将状态约束（如位置、速度、加速度）转化为线性方程
  - 一般形式
  $f^{(k)}(T_j) = x^{(k)}_{j} \\ \Rightarrow\quad \sum_{i\geq k}\frac{i!}{(i-k)!}T_j^{i-k}p_{j,i}=x_{T,j}^{(k)}$
  - 矩阵形式
  $\begin{bmatrix} \cdots & \frac{i!}{(i-k)!}T_j^{(i-k)} & \cdots \\ \vdots & \vdots & \vdots \\ \cdots & \frac{l!}{(l-k)!}T_j^{l-k} & \cdots \end{bmatrix}\begin{bmatrix} p_{j,i}\\ \vdots \\ p_{j,l} \end{bmatrix}=\begin{bmatrix} x_{T_j}^{(k)} \\ \vdots \\ x_{T_j}^{(k)} \end{bmatrix}$
  $\Rightarrow \mathbf{A}_j \mathbf{p}_j = \mathbf{d}_j$
- 段间连续性：如何保证相邻段之间的光滑连接
  - 条件
    $f_j^{(k)}(T_j)=f_{j+1}^{(k)}(T_j)$
  - 推导
    $\sum_{i\geq k}\frac{i!}{(i-k)!}T_j^{i-k}p_{j,i}-\sum_{l\geq k}\frac{l!}{(l-k)!}T_j^{l-k}p_{j+1,l}=0$
  - 矩阵形式
    $\Rightarrow \left[ \mathbf{A}_j - \mathbf{A}_{j+1} \right] \begin{bmatrix} \mathbf{p}_j \\ \mathbf{p}_{j+1} \end{bmatrix} = \mathbf{0}$
凸函数与凸集
- 凸函数 Convex Fuction 的定义
  
  函数 $f:\mathbb{R}^n\mapsto\mathbb{R}$ 是凸函数，当且仅当
  - 定义域 $\mathrm{dom}~f$ 是凸集
  - 对任意 $x,y\in\mathrm{dom}~f$ ， $0\leq\theta\leq1$ ，有
    $f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y)$
    
    函数图像上任意两点之间的弦在图像上方
- 严格凸函数 Strictly Convex：不等式在 $0<\theta<1$ 严格成立
- 凹函数 Concave：若 $- f$ 是凸函数，则 $f$ 是凹函数
- 凸集 Convex Set
  
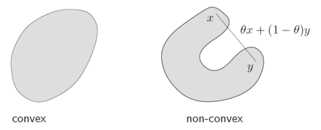
  集合 $C\subseteq\mathbb{R}^n$ 是凸集，若对任意 $x,y\in C$ ， $0\leq\theta\leq1$ ，有
  $\theta x +(1-\theta)y\in C$
  即，集合内任意两点连线仍在集合内。
凸优化问题 Convex optimization
- 标准优化问题形式
  $\begin{aligned} \min_x &\quad f_0(x) \\ \text{s.t.} &\quad f_i(x) \leq 0, \quad i = 1,\dots,m \\ & \quad h_i(x) = 0, \quad i = 1,\dots,p \end{aligned}$
  其中
  - $x\in\mathbb{R}^n$ ：优化变量
  - $f_0$ ：目标函数
  - $f_i$ ：不等式约束函数
  - $h_i$ ：等式约束函数
- 凸优化问题标准形式
  $\begin{aligned} \min_x &\quad f_0(x) \\ \text{s.t.} &\quad f_i(x) \leq 0, \quad i = 1,\dots,m \\ & \quad Ax = b \end{aligned}$
  其中
  - $f_0,f_1,\cdots,f_m$ 是凸函数
  - 等式约束 $A x = b$ 是仿射函数（线性+常数）
- 凸优化问题关键性质
  - 局部最优 = 全局最优：任何局部最优解都是全局最优
  - 大多数问题初始非凸 → 需要重新建模为凸问题
  - 将问题转化为凸形式是一门艺术，没有系统方法
规范凸优化规划 Disciplined convex optimization programs
- 线性规划 Linear Programming（QP）
  $\begin{aligned} \min_x &\quad c^\top x + d \\ \text{s.t.} &\quad Gx \leq h \\ & \quad Ax = b \end{aligned}$
  - 目标函数：仿射（线性）
  - 约束函数：仿射（线性）
  - 特点：最简单，最成熟
- 二次规划 Quadratic Programming（QP）
  $\begin{aligned} \min_x &\quad \frac{1}{2} x^\top P x + q^\top x + r \\ \text{s.t.} &\quad Gx \leq h \\ & \quad Ax = b \end{aligned}$
  - 目标函数：二次 $x^\top Px$
  - 约束函数：仿射（线性）
  - 特点： $P\in S^n \geq 0$ 半正定，常用于最小化加速度
- 二次约束二次规划 Quadratically Constrained QP（QCQP）
  $\begin{aligned} \min_x &\quad \frac{1}{2} x^\top P_0 x + q_0^\top x + r_0 \\ \text{s.t.} &\quad \frac{1}{2} x^\top P_i x + q_i^\top x + r_i \leq 0, \quad i=1,\dots,m \\ & \quad Ax = b \end{aligned}$
  - 目标函数：二次
  - 约束函数：二次不等式
  - 特点： $P_i\in S^n \geq 0$ 半正定，更灵活，如安全区域约束
- 二阶锥规划 Second-Order Cone Programming（SOCP）
  $\begin{aligned} \min_x &\quad f^\top x \\ \text{s.t.} &\quad \|A_i x + b_i\| \leq c_i^\top x + d_i, \quad i=1,\dots,m \\ & \quad Fx = g \end{aligned}$
  - 目标函数：线性
  - 约束函数：二阶锥约束 $|Ax+b|\leq c^\top x+d$
  - 特点：更通用，支持 L1、L2 范数，其它三种规划都可以转化为二阶锥规划

求解凸优化问题的推荐求解器

目标是将轨迹生成问题转化为 Disciplined Convex Optimization Programs，然后使用合适的求解器求解。

求解器	特点	链接
CVX	MATLAB wrapper，写法像数学公式，自动调用底层求解器	http://cvxr.com/cvx/
Mosek	非常稳健，支持几乎所有凸问题，学术免费	https://www.mosek.com/
OOQP	快速、鲁棒的 QP 求解器，开源	http://pages.cs.wisc.edu/~swright/ooqp/
GLPK	快速、鲁棒的 LP 求解器，开源	https://www.gnu.org/software/glpk/

归一化 Normalization：避免数值不稳定问题
- 时间归一化 Time normalization
  - 很短的时间段可能导致数值不稳定，如 $T\rightarrow0$
  - 解决方案 1：将时间缩放到正常范围，如 $[0, 1]$ ；
  - 解决方案 2：使用相对时间线 relative timeline
    $\begin{cases} \sum_{i=0}^N p_{1,i} \left( \dfrac{t-T_0}{T_1-T_0} \right)^i, & T_0 \leq t \leq T_1 \\ \sum_{i=0}^N p_{2,i} \left( \dfrac{t-T_1}{T_2-T_1} \right)^i, & T_1 \leq t \leq T_2 \\ \vdots \\ \sum_{i=0}^N p_{M,i} \left( \dfrac{t-T_{M-1}}{T_M-T_{M-1}} \right)^i, & T_{M-1} \leq t \leq T_M \end{cases}$
- 空间归一化 Spatial normalization
  - 如果场景很大，如 $x = 100.0 m$
  - 可先在一个小规模“沙盒”中求解，再缩放回原尺度
- 这两种操作能显著提高数值稳定性

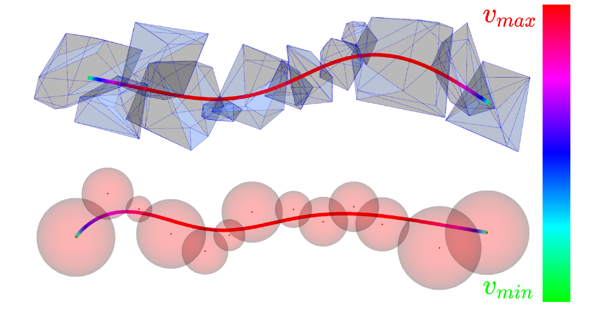
带保证避障的轨迹 Trajectory with Guaranteed Obstacle Avoidance

四步流程
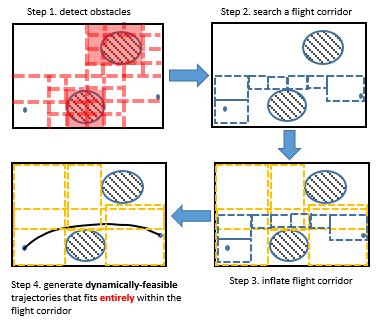
在这里插入图片描述

步骤	描述
detect obstacles	使用传感器检测障碍物（红色圆圈）
search a flight corridor	在地图中搜索一条无碰撞的可行路径（蓝色虚线矩形）
inflate flight corridor	将飞行走廊向外扩展（黄色虚线），形成“安全缓冲区”
generate dynamically-feasible trajectories	在膨胀后的走廊内生成动力学可行的平滑轨迹（黑色曲线）

关键思想：先找“安全通道”，再在里面插值轨迹

将复杂避障问题分解为两个阶段：

几何层：用简单方法（如 A*、RRT）找到一条不碰撞的路径 → 构造飞行走廊
动力学层：在走廊内用凸优化生成满足加速度、速度等约束的平滑轨迹

实现了 “安全 + 动力学可行性 + 实时性” 的统一

两类线性约束
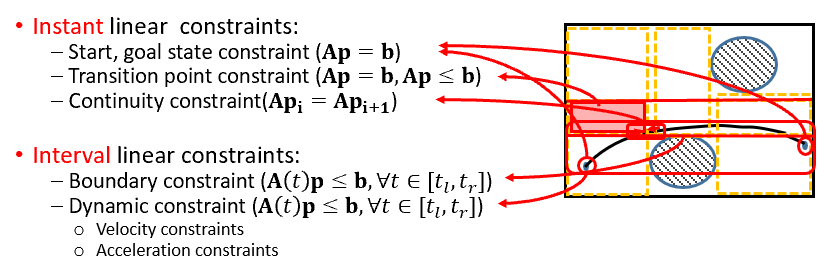
约束类型 1：瞬时线性约束 Instant linear constraints

发生在特定时间点
- 起点、终点状态约束： $\mathbf{A} \mathbf{p} = \mathbf{b}$
- 过度点约束： $\mathbf{A} \mathbf{p} = \mathbf{b},~\mathbf{A} \mathbf{p} \leq \mathbf{b}$
- 段间连续性约束： $\mathbf{A} \mathbf{p}_i =\mathbf{A} \mathbf{p}_{i+1}$
约束类型 2：区间线性约束 Interval linear constraints

对整个时间段成立
- 边界约束： $\mathbf{A}(t) \mathbf{p} \leq \mathbf{b}, \quad \forall t \in [t_l, t_r]$
- 动态约束，如速度、加速度约束： $\mathbf{A}(t) \mathbf{p} \leq \mathbf{b}, \quad \forall t \in [t_l, t_r]$

如何让约束在整个时间区间内都生效？
- 迭代检查极值并添加额外约束
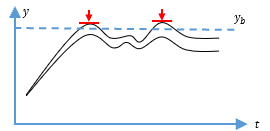
  - 先求解一次轨迹（可能不满足约束）
  - 检查轨迹是否在某处超出安全边界（如 $y(t)>y_b$ ）
  - 若有，则在该点添加一个新约束（如 $y(t^*)\leq y_b$ ）
  - 重新求解 → 再次检查 → 循环直到无违反
  - 缺点：每次都要重新运行优化器，非常耗时；如果根本无解，需要跑很多次才能确认 → 效率低
- 在离散时间点添加大量约束
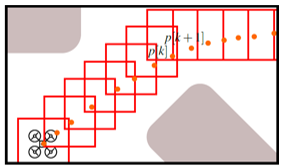
  - 将整个时间段划分为许多小的时间步 time ticks
  - 在每个时间点 $t_k$ ，添加约束
    $\mathbf{A}(t_k)\mathbf{p}\leq\mathbf{b}$
    例如 $\| \dot{r}(t_k) \| \leq v_{\max}, \| \ddot{r}(t_k) \| \leq a_{\max}$
  - 缺点：总是生成更保守过约束的轨迹；约束越多求解器负担越重。
简化带来的问题 Issues of simplification
- 分段轨迹依赖于时间分配
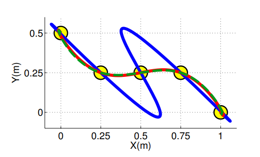
  - 当我们将轨迹分为多个段（如从起点到中间点再到终点），每一段的持续时间会影响整体运动特性。
  - 即使空间路径相同，不同的时间分配会导致速度、加速度完全不同。
- 时间分配显著影响最终轨迹
  - 比如：在两个点之间用短时间通过 → 高速、高加速度
  - 用长时间通过 → 低速、平滑
- 如何获得合适的时间分配？
  - 这是优化的核心问题之一
  - 常见做法：将时间作为优化变量（time parameterization optimization）
- 梯形速度曲线
  
  这种模型在单一路径段上看起来很“傻”，但是在基于走廊的轨迹生成中效果很好。
  
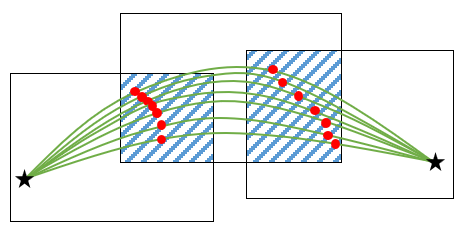
  走廊之间的重叠区域提供了很大的自动调整空间，允许系统灵活选择最佳路径。

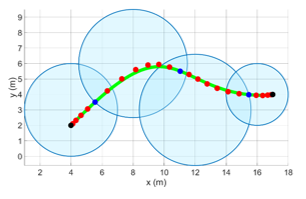
5.5.2 空间-时间变形轨迹优化方法 Spatial-Temporal Deformation

空间-时间变形模型
- 优化问题的数学形式
  $\begin{aligned} & \min_{z(t), T} \int_0^T v(t)^\top \mathbf{W} v(t)\, dt + \rho(T), \\ & \text{s.t.} \quad v(t) = z^{(s)}(t), \quad \forall t \in [0, T], \\ & \quad\quad \mathcal{G}(z(t), \dot{z}(t), \dots, z^{(s)}(t)) \leq \mathbf{0}, \quad \forall t \in [0, T], \\ & \quad\quad z(t) \in \mathcal{F}, \quad \forall t \in [0, T], \\ & \quad\quad z^{[s-1]}(0) = \bar{z}_o, \quad z^{[s-1]}(T) = \bar{z}_f, \\ & \quad\quad z^{[s-1]} := (z^\top, \dot{z}^\top, \ddot{z}^\top, \dots, z^{(s-1)\top})^\top. \end{aligned}$
- 图示
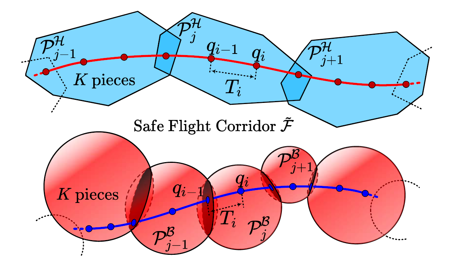
- 核心思想：将轨迹视为一个可变形的“橡皮筋”，可以在空间和时间上同时调整，以满足约束。
  - 空间变形：改变路径形状（如绕开新出现的障碍物）
  - 时间变形：调整各段速度（如减速通过狭窄区域）
性能评估
- 计算效率高
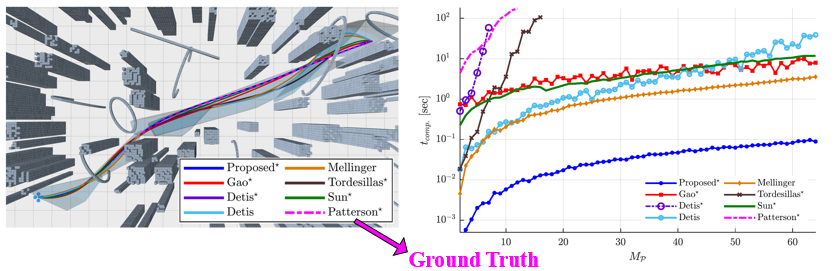
- 轨迹更平滑、更短、更贴近理想路径
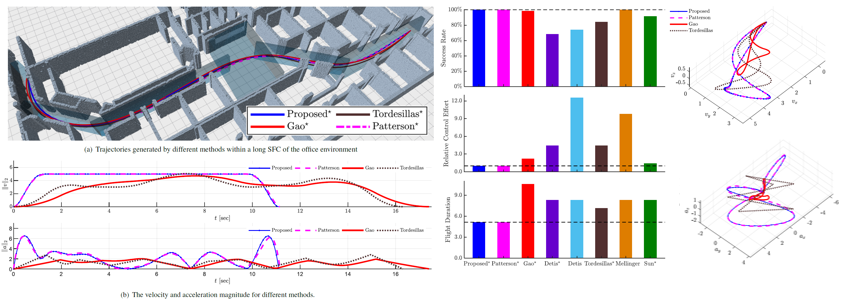
- 系统自动调节速度，在狭窄区域减速，在开阔区域提速