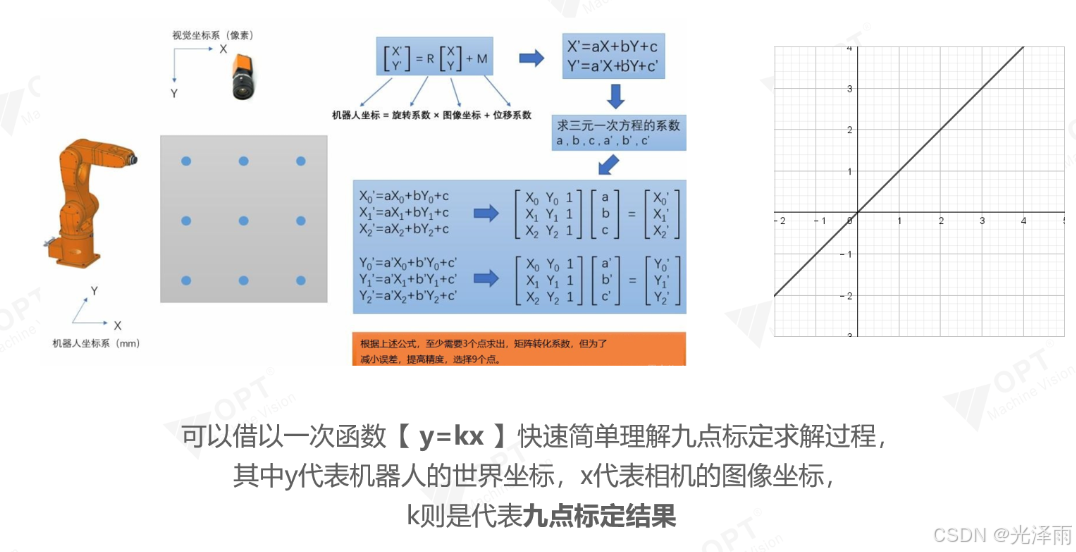
如何让机器人知道相片里的像素点（Pixel）对应现实世界中的哪个位置（mm）。

📐 九点标定原理拆解

这张图通过类比初中数学的一次函数，将复杂的仿射变换（Affine Transformation）通俗化了：

1. 核心公式类比

图中提到 y = kx。

• x(输入)：相机的图像坐标（像素单位），即你在 Smart3 软件里识别出的特征中心点。

• y (输出)：机器人的世界坐标（毫米单位），即 PLC 最终需要的物理坐标。

• k (结果)：这就是九点标定求出的“转换算子”（一个包含旋转、平移和缩放的矩阵）。

2. 数学公式的深度拆解

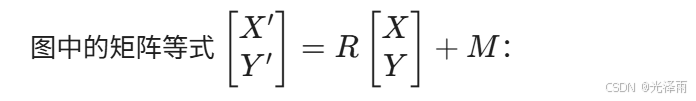
• 旋转与缩放 (R)：解决相机装歪了、或者像素与毫米比例不一致的问题。

• 平移 (M)：解决相机中心点和机器人原点不重合的问题。

• 三元一次方程组：

  • 为了求出 $a, b, c$（控制 X 方向转换）和 $a', b', c'$（控制 Y 方向转换）这 6 个未知数，理论上至少需要 3 组点。

  • 为什么要九个点？ 为了通过最小二乘法减少机械误差和镜头畸变带来的偶然误差。九个点能提供足够的冗余，让结果更精准。

  现场实操的关键注意事项

  1. 标定板位姿：九个点要尽量铺满相机视野的 70%-80%。如果你的九个点只缩在画面中心小小的一个方块里，边缘的精度会烂得一塌糊涂。

  2. 顺序一致性：机器人的 1-9 号点位动作顺序，必须与 Smart3 软件中识别像素点的 1-9 号顺序严格对应，否则算出来的矩阵是乱的，机器会往反方向跑。

  3. 高度一致性：标定时，标定板的高度必须和你实际生产时产品的高度完全一致（这就是所谓的“共面”）。高度差 1mm，精度可能差出几百个丝。

没有明白三个点是如何确定转换关系的

1. 为什么“1个点”不行？

如果你只告诉我一个像素坐标 $(100, 100)$ 对应机械坐标 $(50, 50)$，我只知道位置。但我不知道你的相机是不是歪了（旋转），也不知道 1 个像素到底代表 1 毫米还是 10 毫米（缩放）。

2. 为什么“2个点”还是不够？

有了两个点，我可以算出：

• 距离（缩放）：两个点之间的像素距离 vs 物理距离，比例就出来了。

• 角度（旋转）：两个点连线的斜率，旋转角度也就出来了。

• 但是，工业相机的轴向可能存在非等比例缩放（比如由于安装倾斜，导致 X 方向 1 像素代表 0.1mm，而 Y 方向 1 像素代表 0.11mm）。

3. 为什么“3个点”是最低要求？

看图里那个三元一次方程组：

$$X' = aX + bY + c$$

$$Y' = a'X + b'Y + c'$$

这里一共有 6 个未知数（$a, b, c, a', b', c'$）。

在数学上，要解出 6 个未知数，你需要 6 个独立的方程。

• 1 个点提供 2 个方程（一个 X'，一个 Y'）。

• 3 个点正好提供 $3 \times 2 = 6$ 个方程。

通过这三个点，算法可以锁定：

1. 平移 (Translation)：确定原点的偏移。

2. 旋转 (Rotation)：确定坐标系的偏转角。

3. 缩放 (Scaling)：确定 X 和 Y 方向各自的单位换算比例。

4. 倾斜 (Shear)：确定坐标轴是否垂直（修正安装带来的拉伸变形）。

---

🛠️ 工业现场实操案例

想象你在大族贝瑞调一台激光打标机：

• 点 1：你告诉系统，画面左上角是 $(0,0)mm$。

• 点 2：你告诉系统，右边那个点是 $(100,0)mm$。此时系统知道 X 轴的方向和比例了。

• 点 3：你告诉系统，下面那个点是 $(0,100)mm$。此时系统知道 Y 轴的方向，并且确认了 X 和 Y 是否垂直。

标注关键注意事项：

在现场，我们严禁只用三个点。因为机械手每次移动都有误差。如果你只取 3 个点，其中任何一个点因为震动或反光偏移了 1 个像素，整个坐标系就全歪了。

九点标定的意义在于，它用 9 组数据去解这 6 个未知数。利用最小二乘法（一种数学优化手段），让这 6 个未知数能“兼顾”所有 9 个点，从而把某个点的偶然误差平摊掉，让系统变稳。

X‘为什么不等于aX

假设X’ Y‘是物理坐标，X Y是像素坐标，我不明白X’为什么要用aX+bY+c表示，X对应着X‘ 它们之间有一个系数关系就好了，上面的仿射矩阵R代表的什么，我学过线性代数，但是好多都忘了。

1. 为什么 $X'$ 不能只用 $aX$ 表示？

你直觉认为 $X$ 对应 $X'$，这在相机坐标系和机械坐标系完美平行的情况下是对的。但工业现场充满了“意外”：

• 旋转（最核心原因）：想象一下，你的相机装歪了 $45^\circ$。当你让电机只沿水平 $X'$轴挪动 10mm 时，在相机画面里，目标点不仅在 $X$ 方向动了，在 $Y$ 方向也动了！

• 物理意义：$bY$ 这个项的存在，就是为了补偿“旋转”。它代表了 Y 方向的像素位移对 X 方向物理距离的影响贡献。

• 平移补偿：末尾的 $c$ 就是线性代数里的偏置，代表了两个坐标系原点之间的偏移量。

所以，$X' = aX + bY + c$ 实际上描述的是：物理世界的 X 坐标，是由像素世界的 X 位移、Y 位移以及初始偏差共同决定的。

---

2. 仿射矩阵 $R$ 到底代表什么？

你提到的矩阵 $R$，在线性代数里叫变换矩阵。在九点标定中，它其实是一个“多功能组合包”：

• 旋转 (Rotation)：把相机的画面“旋正”到和机械手一致。

• 缩放 (Scaling)：把“像素单位”转换成“毫米单位”。

• 错切 (Shearing)：修正相机安装不垂直导致的图像拉伸。

当你写

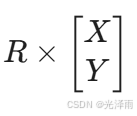
时，你实际上是在做基坐标变换。

---

3. 回忆线性代数：3个点如何定乾坤？

你还记得解方程组吗？

我们要找的其实是这 6 个参数：$a, b, c$（控制 $X'$）和 $a', b', c'$（控制 $Y'$）。

当我们有 3 个点时，我们会得到一个非齐次线性方程组：

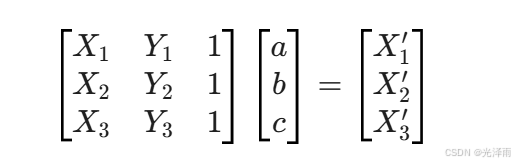
重点来了： 只要这三个点不在同一直线上（即左边的矩阵是可逆的），你就能通过矩阵求逆，唯一确定 $a, b, c$。