MetaWorld——分层世界模型：融合 VLM 的语义推理能力、预测的未来动态环境、模仿学习的先验，及基于模型RL的对动态环境的在线自适应

v_JULY_v

448人浏览 · 2026-02-07 18:14:29

v_JULY_v · 2026-02-07 18:14:29 发布

前言

我个人比较看好分层架构和世界模型，故有了本文

第一部分

1.1 引言与相关工作

1.1.1 引言

如原论文所说，人形机器人作为具身智能的典型体现，长期面临一个根本性挑战：在非结构化和动态环境中执行由语义驱动的行走-操作任务

在这一挑战的核心，是当前机器人控制系统中存在显著的” 抽象鸿沟”——高层语义理解与低层物理执行之间的脱节Kunze et al. (2011); Huanget al. (2024); Geng et al. (2024); Zhang et al. (2024)

一方面，以视觉-语言模型(VLMs)为代表的大规模模型在高层任务规划和语义推理方面展现出卓越能力，能够理解” 做什么”
另一方面，基于模仿学习或强化学习的低层控制方法可以生成精确的关节级动作，用于解决” 如何去做”
然而，缺乏一个统一且可扩展的框架来弥合这些不同能力之间的鸿沟，往往会导致语义规划与物理约束相脱节
相反，低层控制策略往往又缺乏足够的通用性，难以在复杂的、由多种高层任务构成的场景中实现泛化

当前主流方法在解决这一问题时各自存在明显局限

尽管端到端强化学习在理论上有能力发现最优策略，但其对样本的需求往往极其低效，使其在真实机器人平台上难以实际应用(Song & Chen, 2024)
模仿学习虽然能够从人类示范中有效获取自然的运动模式，但通常得到的策略鲁棒性有限，对环境波动和外部扰动依然高度敏感(Lesort et al., 2024)
将视觉-语言模型(VLMs)直接用于机器人控制则会面临严重的“符号落地”问题，其生成的动作规划往往在运动学或动力学上难以实现

尽管现有工作探索了这些方法的集成，但多数方案仍局限于简单的任务级串联，或松散耦合的独立模块组合，未能构建真正统一的、分层的交互架构(Pan et al., 2025; Li et al., 2025b; Shen et al., 2025)

为系统性地解决上述挑战，来自1Beijing University of Technology、2Fudan University、3Tsinghua University的研究者提出了 MetaWorld

具体而言，这是一个基于分层世界模型的机器人控制框架。该框架协同融合了 VLM 的语义推理能力、来自模仿学习的运动先验，以及源自基于模型强化学习的在线自适应机制，从而构建出一条连贯且可扩展的流水线，有效弥合高层语义推理与低层物理执行之间的鸿沟

1.1.2 相关工作

首先，对于机器人中的世界模型

世界模型通过预测环境状态转移来促进策略学习，已成为提升机器人领域样本效率和泛化能力的关键工具（Li et al., 2025a）

主流方法（例如 Dreamer 系列（Hafner et al.,2020; 2021; 2025b;a））通过潜在空间预测来进行策略优化
而基于模型的强化学习方法例如，TD-MPC2 Hansen et al. (2024) 在复杂动态环境中进一步实现了高性能控制
然而，大多数现有的世界模型缺乏层级深度，难以将高层语义任务分解为可执行的物理动作序列，从而限制了其在长时间跨度、多步具身任务中的直接应用 Fujii & Murata (2025)

本文提出的分层世界模型架构在语义规划层与物理执行层之间引入了显式的分离，使世界模型能够同时处理语言指令的语义解析和物理环境的动态预测，从而有效弥合任务规划与动作生成之间的鸿沟

其次，对于技能迁移学习

迁移学习通过系统复用预先获得的技能来促进机器人的泛化能力

目前的机器人控制方法包括：

采用域适配（例如域随机化）来弥合从仿真到现实（sim-to-real）的鸿沟（Jiang et al., 2024）
利用策略微调（例如 progressive networks）进行局部调整（Fehring et al., 2025）
以及采用元学习（例如 MAML）实现快速的小样本自适应（Finn et al., 2017；Kayaalp et al., 2022）

然而，这些方法面临两个主要瓶颈：

一是严重依赖目标域数据或多阶段训练，从而限制了其在实际中的部署；
二是在动态扰动下无法实现实时的、毫秒级的自适应

为了解决这些问题，作者提出了一种动态专家选择与运动先验融合机制

作者宣称，通过构建多专家策略库，他们的方法在模型预测控制（MPC）框架内动态选择最相关的策略，从而实现实时策略调整

该方法在保持专家策略效率的同时，显著提升了在非结构化环境中的适应性和泛化能力

最后，对于VLM 在实时任务解析中的应用

视觉-语言模型（VLM）在开放词汇感知、场景理解和高层推理方面展现出卓越能力，已被广泛用于机器人高层任务规划和语义引导

代表性工作如 VIMA 和 RT-2试图直接利用 VLM 生成机器人动作序列，或将其作为符号规划器的前端（Brohanet al., 2023; Huang et al., 2024）
然而，这类方法普遍面临“符号落地（symbolgrounding）”问题：VLM 生成的计划往往忽略机器人的运动学与动力学约束以及环境物理规律，导致生成的计划在物理上不可行

在本工作中，作者通过将 VLM 的角色限制在高层语义解析上，并把其输出映射到一组预先验证、在物理上可行的专家策略上，从而缓解 VLM 的物理局限

同时，作者的框架利用 VLM 在语义理解和任务分解方面的优势来处理开放式环境语义，并在训练过程中通过闭环反馈实现动态重规划，使复杂任务的执行能够以基础专家策略为参照

1.2 MetaWorld的完整方法论

1.2.1 MetaWorld 分层架构

如下图所示

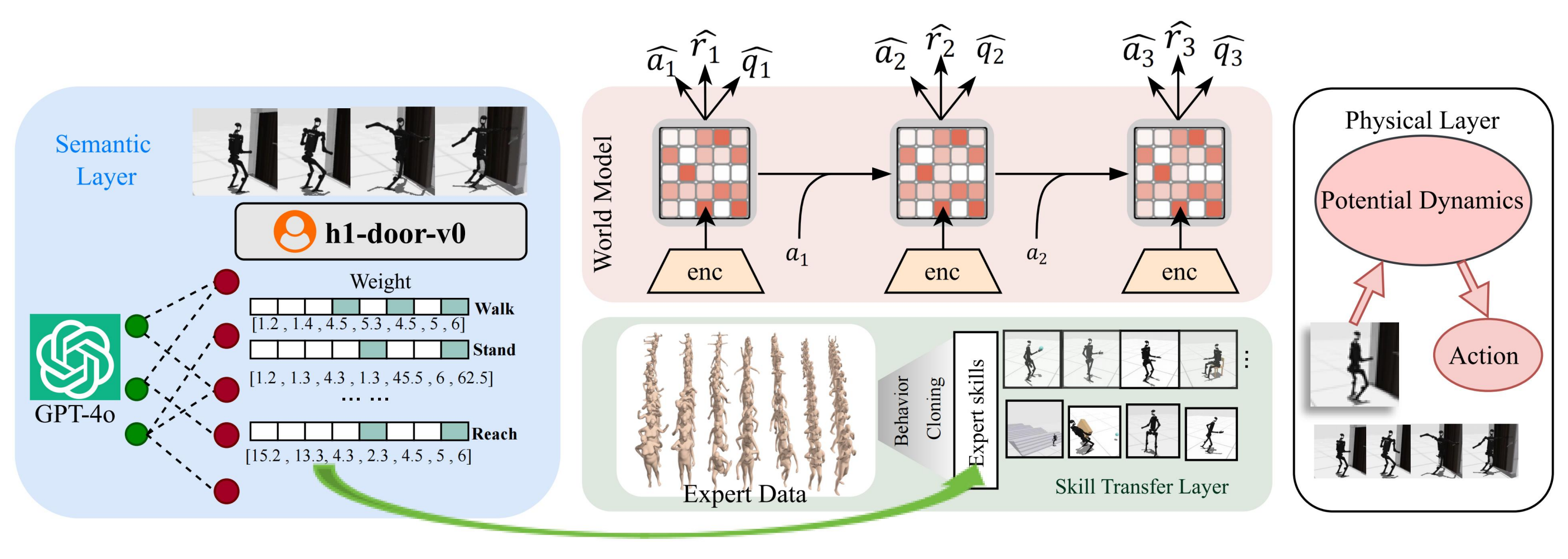
该图展示了 MetaWorld 框架的三层架构：

语义层通过视觉-语言模型将观测解析为可执行的技能序列
技能迁移层通过分层世界模型整合专家策略先验并实现动态适应
物理层在紧凑的状态空间中利用潜在动力学模型执行精确控制

MetaWorld 的核心思想是将机器人控制问题分解为两个不同的层次：

一个是负责解释任务意图的语义规划层
另一个是负责生成物理上可行动作的物理执行层

这个分层设计可以形式化为：

$\pi\left(a_{t} \mid s_{t}, \mathcal{T}\right)=\pi_{\mathrm{phys}}\left(a_{t} \mid s_{t}, \pi_{\mathrm{sem}}(\mathcal{T})\right)$

其中 $\pi_{\mathrm{sem}}$ 将任务描述 $\mathcal{T}$ 映射为语义规划，而 $\pi_{\text {phy }}$ 根据当前状态 $s_{t}$ 和语义规划生成具体动作 $a_{t}$

这种架构使语义理解和物理控制组件能够在保持整体最优性的同时分别进行优化

优化目标是最大化期望累计回报

$J(\pi)=\mathbb{E}\left[\sum \gamma^{t} r\left(s_{t}, a_{t}\right)\right]$

其中分层优化有效地解决了语义层面和物理层面上各自不同的挑战

1.2.2 语义规划与符号落地

语义规划层采用视觉-语言模型（Vision-Language Model, VLM）将自然语言任务描述映射到专家策略权重

不同于传统方法，作者将 VLM 的输出限制为一个专家权重向量 $w$ ，而不是直接输出动作

$\mathbf{w}=f_{\mathrm{VLM}}(\mathcal{T}, \mathcal{E})$

该设计的关键创新在于将符号扎根问题转化为专家策略的线性组合

VLM 通过精心设计的提示生成专家权重，将响应R 经过解析函数处理以获得归一化权重

$w_{i}= \exp \left(\operatorname{extract}_{i}(R)\right) / \sum_{j} \exp \left(\operatorname{extract}_{j}(R)\right)$

由于每个专家策略 $\pi_{\exp }^{i}$ 在物理上都是可行的，生成的语义规划 $\pi_{\mathrm{sem}}(\mathcal{T})=\sum_{i} w_{i} \pi_{\mathrm{exp}}^{i}$ 自然满足物理约束

且符号扎根误差被限制在专家策略差异的范围内，显著优于直接动作生成方法

1.2.3 动态自适应机制

为应对动态环境变化，作者引入一种状态感知的专家选择机制

基于当前状态 $s_{t}$ ，作者构建一个选择概率分布：

$p\left(i \mid s_{t}\right)=\frac{\exp \left(\phi\left(s_{t}\right)^{\top} \psi\left(\pi_{\exp }^{i}\right)\right)}{\sum_{j=1}^{K} \exp \left(\phi\left(s_{t}\right)^{\top} \psi\left(\pi_{\exp }^{j}\right)\right)}$

其中 $\phi$ 是状态编码函数， $\psi$ 是专家特征提取函数

由VLM 生成的语义权重 $w_{i}$ 与动态选择概率 $p\left(i \mid s_{t}\right)$ 进行融合，以获得最终权重

$\tilde{w}_{i}\left(s_{t}, \mathcal{T}\right)=\alpha w_{i}+(1-\alpha) p\left(i \mid s_{t}\right)$

该融合机制在理论上结合了长期任务规划和短期状态自适应的优势

参数 $\alpha \in[0,1]$ 控制语义规划与状态感知的相对重要性，通过适当调整 $\alpha$ ，在任务一致性与环境适应性之间实现平衡

参考专家动作

$a_{\mathrm{ref}}=\sum_{i} \tilde{w}_{i}\left(s_{t}, \mathcal{T}\right) \pi_{\exp }^{i}\left(s_{t}\right)$

则为物理执行层提供了高质量的初始解

1.2.4 物理执行与在线优化

物理执行层采用TD-MPC2 算法，为模型预测控制（MPC）构建潜在动力学模型。观测值 $o_{t}$ 被编码为潜在状态 $z_{t}=f_{\text {enc }}\left(o_{t}\right)$ ，并通过动力学模型 $z_{t+1}=f_{\mathrm{dyn}}\left(z_{t}, a_{t}\right)$ 预测状态演化

MPC 优化问题求解未来时域 $H$ 上的最优动作序列：

$\mathbf{a}_{t: t+H-1}^{*}=\arg \max _{\mathbf{a}_{t: t+H-1}} \mathbb{E}\left[\sum_{k=0}^{H-1} \gamma^{k} r\left(z_{t+k}, a_{t+k}\right)+\gamma^{H} V\left(z_{t+H}\right)\right]$

由专家引导的动作 $a_{\text {ref }}$ 被并入优化目标

$\mathcal{L}_{\text {total }}=\mathcal{L}_{\mathrm{TD}}+\lambda\left\|a_{t}-a_{\mathrm{ref}}\right\|^{2}$

其中时序差分（Temporal-Difference, TD）学习损失

$\mathcal{L}_{\mathrm{TD}}=\mathbb{E}\left[\| Q\left(z_{t}, a_{t}\right)-\left(r_{t}+\right.\right.\left.\left.\gamma Q\left(z_{t+1}, \pi\left(z_{t+1}\right)\right)\right) \|^{2}\right]$

保证对价值函数的精确估计

该设计在利用专家知识加速学习过程的同时，保持了在线适应能力。TD-MPC2 采用分位数回归来学习价值函数，通过最小化TD 误差实现策略改进

1.2.5 理论分析与实现

基于压缩映射理论，作者在适当的参数选择下证明了算法的收敛性。价值迭代算子 $\hat{\mathcal{T}}$ 满足收缩性质 $\left\|\mathcal{T} Q_{1}-\mathcal{T} Q_{2}\right\|_{\infty} \leq\gamma\left\|Q_{1}-Q_{2}\right\|_{\infty}$ , 从而保证价值函数收敛到最优解

与传统方法相比, 样本复杂度由 $\mathcal{O}\left(|\mathcal{S}||\mathcal{A}| /\left[(1-\gamma)^{2} \epsilon^{2}\right]\right)$ 降低为 $\mathcal{O}(1 /[(1-\left.\left.\gamma)^{2} \epsilon^{2}\right]+K\right)$ , 体现了知识复用的效率优势