本文主要针对计算机相关专业的同学，你们已经具备了基础的python或者C++编程基础，数学方面也该有所见解。本章主要介绍数学知识里的一些重点以及学习路径。

一、线性代数

学之前我们得先知道线性代数在机器人领域中的作用，在机器人中，线性代数主要适用于：

1、机器人运动学（正运动学、逆运动学）中的坐标变换，使用齐次变换矩阵（4x4矩阵）表示旋转和平移。

2、机器人动力学（牛顿-欧拉方程、拉格朗日方程）中的矩阵运算。

3、状态估计（如卡尔曼滤波）中的协方差矩阵、状态转移矩阵、观测矩阵等。

4、计算机视觉中的相机模型（内参矩阵、外参矩阵）、三维点重建等。

5、路径规划中的空间表示（如占据栅格地图）和优化问题。

因此，我们需要重点学习以下内容：

一、向量和矩阵的基本运算

1. 向量加法

• 定义：两个向量相加，即对应分量相加。
  若向量 a=(a1,a2,a3)，b=(b1,b2,b3)，则a+b=(a1+b1,a2+b2,a3+b3)。

• 几何意义：遵循平行四边形法则或三角形法则，表示位移的叠加。

2. 标量乘法

• 定义：一个标量k与向量 a=(a1,a2,a3)相乘，即每个分量乘以k：ka=(ka1,ka2,ka3)。

• 几何意义：缩放向量的长度，若 k<0则方向反向。

3. 点积（内积）

• 定义：两个向量的点积是一个标量，计算为对应分量乘积之和。

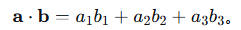
• 几何意义：a⋅b=∣a∣∣b∣cos⁡θ，其中θ为夹角。可用于判断垂直性和投影。

4. 叉积（向量积）

• 定义：仅适用于三维向量，结果是一个向量。

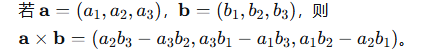
• 几何意义：结果向量垂直于a和b，方向由右手定则确定，长度 ∣a×b∣=∣a∣∣b∣sin⁡θ，表示以a、b为边的平行四边形面积。

5. 矩阵加法

• 定义：只有同型矩阵（行数和列数分别相等）才能相加。对应位置的元素相加。

• 计算：

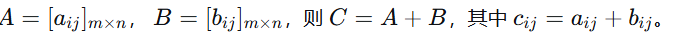
• 条件：必须同型。

• 性质：

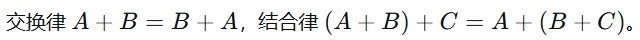
• 示例：

  

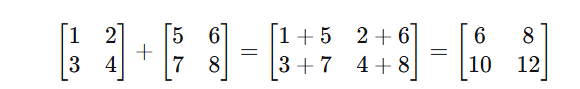
6. 矩阵乘法

这是最重要且最容易出错的运算。

• 定义：矩阵A与B相乘，要求A的列数等于B的行数。结果矩阵C的行数等于A的行数，列数等于B的列数。

• 计算：若A是m×p矩阵，B是p×n矩阵，则C=A×B是m×n矩阵。其中C的第i行第j列元素Cij等于A的第i行向量与B的第j列向量的点积。

  

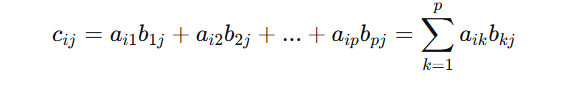
• 条件：A的列数 = B的行数。

• 重要性质：

  • 不满足交换律：绝大多数情况下 AB≠BA。

  • 满足结合律：(AB)C=A(BC)

  • 满足分配律：A(B+C)=AB+AC， (B+C)A=BA+CA。

• 示例：

  

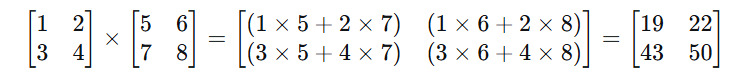
  注意：如果反过来乘，维度可能不匹配，即使匹配结果也不同。

  

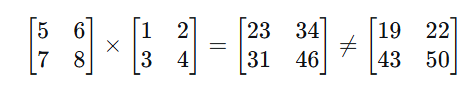
7. 矩阵的转置

8. 矩阵的逆

• 

  验证：

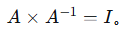
二、矩阵的行列式、特征值和特征向量

• 特征向量 是在这个变换下方向保持不变的向量（只被拉伸或压缩，不旋转）

• 特征值 是这个特征向量被拉伸或压缩的倍数

• 数学定义：对于方阵A，如果存在非零向量v和标量λ，使得：Av=λv。则λ称为A的特征值，v称为对应于λ的特征向量。

• 计算步骤

• 1.求特征值

• 特征值通过解特征方程得到：det⁡(A−λI)=0

  其中I是单位矩阵，det表示行列式。

  特征多项式：det⁡(A−λI)是λ的n次多项式。
  2、求特征向量

  对每个特征值λi​，解齐次线性方程组：

  

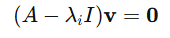
  所有非零解都是对应于λi的特征向量。

• 示例
  
  

• 重要性质
  
  

• 矩阵对角化
  

• 几何解释
  

• 注意事项

        1、特征向量必须是非零向量
        2、特征值可以是复数（即使矩阵元素都是实数）
        3、重特征值可能对应多个线性无关的特征向量，也可能只对应一个
        4、不是所有矩阵都可对角化（当线性无关特征向量少于 nn 时）

三、矩阵的分解

LU分解，QR分解，SVD分解，奇异值分解

1、LU分解

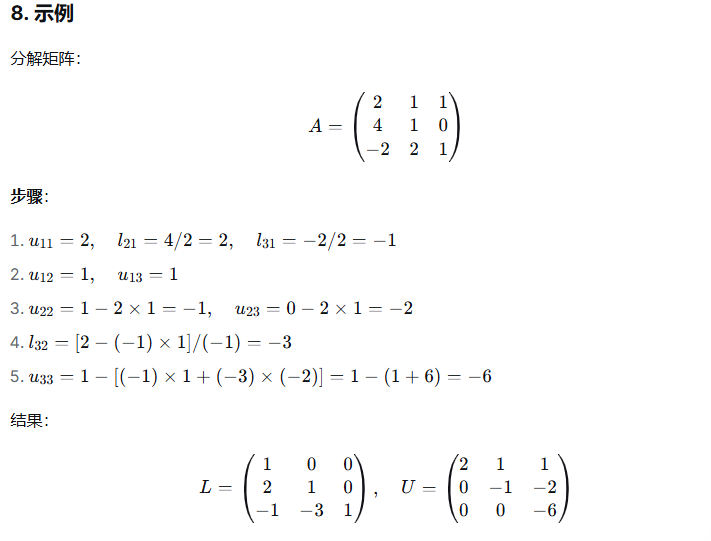
2、QR分解

3、SVD分解

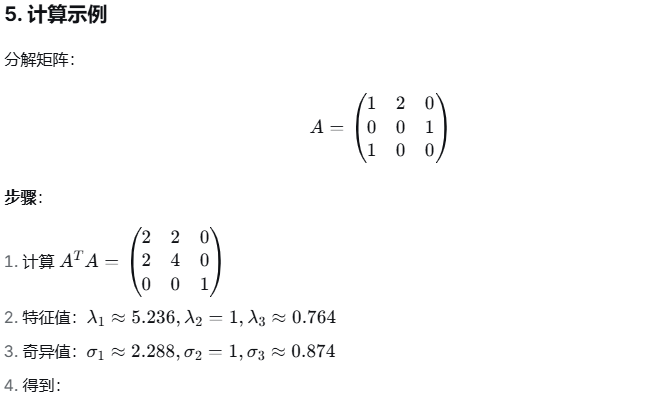
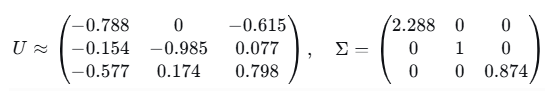
4、特征值分解