深度强化学习算法：DDPG TD3 SAC 实验环境：机器人MuJoCo

本文针对在 MuJoCo 的 HalfCheetah-v2 环境中实现的四种深度强化学习算法进行全面分析，包括 A3C、DDPG、SAC 和 TD3。这些算法代表了现代深度强化学习在连续控制任务中的主要技术路线。

算法架构概览

1. A3C（异步优势行动者-评论者）算法

A3C 算法采用分布式架构，通过多个并行的智能体实例同时与环境交互，共同更新全局网络参数。

核心架构特点：

• 共享的全局神经网络和多个工作节点的本地网络
• 使用多进程并行处理，充分利用多核 CPU 资源
• 每个工作节点独立收集经验并计算梯度，定期同步到全局网络

网络结构设计：

class ACNet(nn.Module):
    def __init__(self, inputSize, hiddenSize, outputSize):
        super(ACNet, self).__init__()
        # 共享的特征提取层
        self.linear1 = nn.Linear(inputSize, hiddenSize)
        
        # 行动者网络分支
        self.actor1 = nn.Linear(hiddenSize, hiddenSize // 2)
        self.mu = nn.Linear(hiddenSize // 2, outputSize)  # 均值输出
        self.sigma = nn.Linear(hiddenSize // 2, outputSize)  # 标准差输出
        
        # 评论者网络分支
        self.critic1 = nn.Linear(hiddenSize, hiddenSize // 2)
        self.value = nn.Linear(hiddenSize // 2, 1)  # 状态价值输出

行动者网络输出动作的均值和标准差，使用高斯分布进行随机策略采样，评论者网络评估状态价值函数。

2. DDPG（深度确定性策略梯度）算法

DDPG 结合了确定性策略梯度和深度 Q 网络的特点，适用于连续动作空间的控制问题。

核心机制：

• 行动者-评论者架构，行动者学习确定性策略，评论者学习动作价值函数
• 使用目标网络提高训练稳定性
• 采用经验回放机制打破数据相关性
• 添加奥恩斯坦-乌伦贝克过程噪声进行探索

网络更新策略：

def _updateParams(self, t, s, isSoft=False):
    for t_param, param in zip(t.parameters(), s.parameters()):
        if isSoft:
            # 软更新：目标网络参数缓慢跟踪在线网络
            t_param.data.copy_(t_param.data * (1.0 - self.tau) + param.data * self.tau)
        else:
            # 硬更新：直接复制参数
            t_param.data.copy_(param.data)

3. SAC（软演员-评论者）算法

SAC 是一种最大熵强化学习算法，在标准奖励最大化的基础上增加了策略熵最大化目标。

深度强化学习算法：DDPG TD3 SAC 实验环境：机器人MuJoCo

算法特色：

• 自动熵调节：动态调整温度参数平衡奖励和熵
• 使用两个 Q 网络减少价值高估
• 随机策略与重参数化技巧
• 结合了离策略学习和随机策略优化的优势

核心损失函数：

• 评论者损失：最小化时序差分误差
• 行动者损失：最大化期望回报和策略熵
• 熵温度损失：自动调节熵权重

4. TD3（双延迟深度确定性策略梯度）算法

TD3 是 DDPG 的改进版本，通过三项关键技术解决价值高估问题。

关键技术改进：

1. 双 Q 学习：使用两个独立的 Q 网络，取最小值作为目标
2. 目标策略平滑：在目标行动者输出添加噪声，平滑价值估计
3. 延迟策略更新：策略网络更新频率低于价值网络

# 目标 Q 值计算采用双网络最小值
target_Q1, target_Q2 = self.critic_target(next_state, next_action)
target_Q = torch.min(target_Q1, target_Q2)
target_Q = reward + not_done * self.discount * target_Q

实验设计与性能分析

训练配置

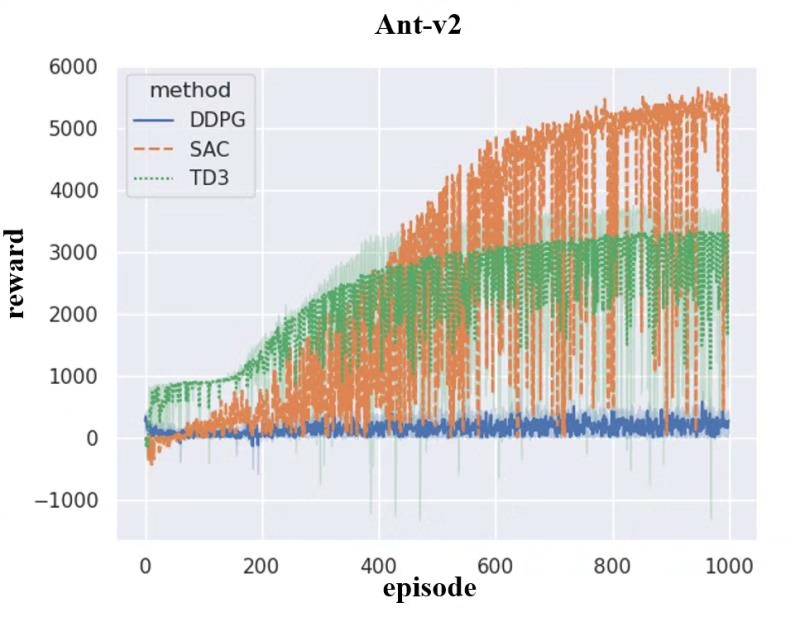
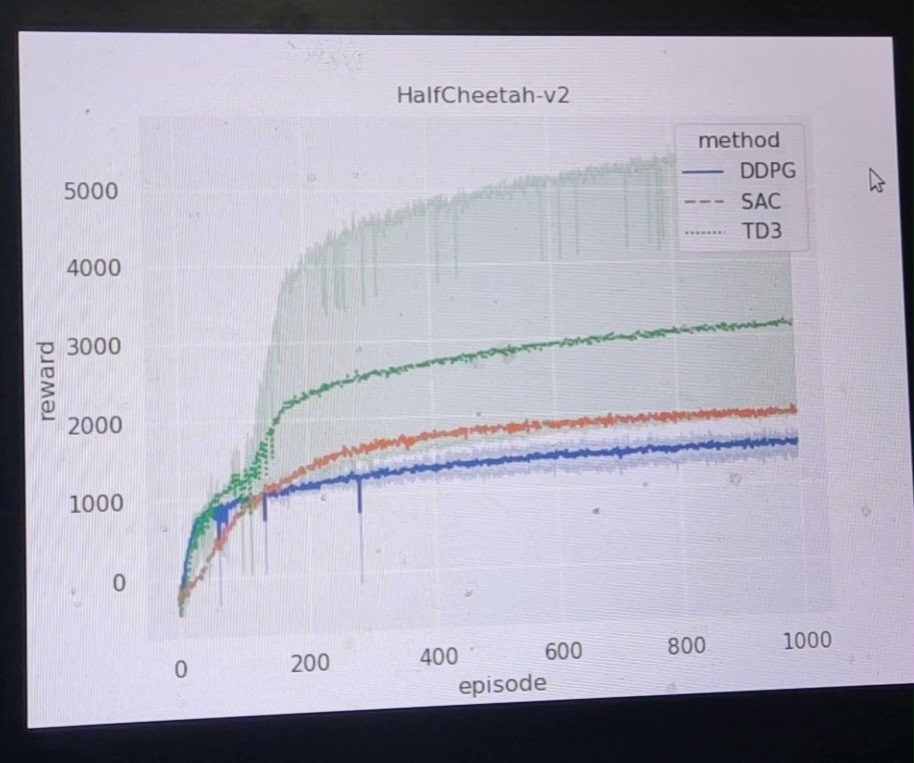
所有算法在 HalfCheetah-v2 环境中进行训练，该环境要求智能体学习奔跑技能以获得高速移动奖励。实验设置了统一的训练轮次（1000-3000 回合）和评估标准，确保公平比较。

性能表现

根据实验结果可视化分析：

1. 收敛速度：SAC 和 TD3 表现出较快的初期学习速度
2. 最终性能：SAC 算法在长期训练中达到最高平均回报
3. 稳定性：TD3 由于采用了多种稳定化技术，训练过程最为稳定
4. 样本效率：DDPG 和 TD3 由于使用经验回放，具有较好的样本效率

算法适用场景分析

• A3C：适用于分布式计算环境，不需要经验回放，适合在线学习场景
• DDPG：确定性策略，适合需要精确控制的场景，但需要仔细调节超参数
• SAC：随机策略，探索效率高，对超参数相对鲁棒，适合复杂环境
• TD3：在 DDPG 基础上改进，训练更稳定，适合对稳定性要求高的应用

实现细节与优化技巧

网络结构优化

所有算法均采用深度神经网络作为函数逼近器，隐藏层使用 ReLU 或 Leaky ReLU 激活函数，输出层根据任务需求使用不同的激活函数：

• 连续动作空间：tanh 激活函数将输出限制在有效范围内
• 价值输出：线性激活函数
• 策略标准差：softplus 激活函数确保正值

探索策略设计

• A3C：通过策略网络的随机性自然探索
• DDPG：添加时间相关的 OU 噪声
• SAC：最大熵原则引导的随机策略
• TD3：在目标策略中添加截断噪声

训练稳定性措施

• 梯度裁剪防止梯度爆炸
• 目标网络减少训练不稳定性
• 经验回放打破数据相关性
• 适当的学习率调度

结论

在 HalfCheetah-v2 连续控制任务中，SAC 和 TD3 算法表现出色，这主要归功于它们在算法设计上对稳定性和样本效率的优化。SAC 的最大熵框架使其在探索和利用之间取得良好平衡，而 TD3 通过多项技术创新有效解决了价值高估问题。

实际应用中，算法选择应基于具体任务需求：对样本效率要求高的场景可优先考虑 TD3，对最终性能要求极高的场景可选用 SAC，分布式计算环境可考虑 A3C，而对确定性策略有特殊需求时可使用 DDPG。

这些算法的成功实现为复杂连续控制问题提供了有效的解决方案，也为进一步研究深度强化学习在机器人控制等领域的应用奠定了坚实基础。