蓝桥杯算法练习
本文汇总了蓝桥杯多个题目的解题思路与代码实现,包括油漆面积、分考场、合根植物、区间移位、填字母游戏、碱基、机器人塔、压缩变换、取球博弈和交换瓶子等题目。每个题目都提供了详细的算法分析和优化策略,如贪心算法、DFS回溯、并查集、记忆化搜索等。
目录
蓝桥杯105 油漆面积
#include <bits/stdc++.h>
using namespace std;
const int MAX = 10001; // 坐标范围0~10000,数组开10001足够
bool covered[MAX][MAX] = {false}; // 标记方格是否被覆盖,初始全为false
int main() {
int n;
cin >> n;
for (int k = 0; k < n; k++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
// 确保x1<x2,y1<y2(处理对角点顺序问题)
if (x1 > x2) swap(x1, x2);
if (y1 > y2) swap(y1, y2);
// 遍历矩形内的每个单位方格,标记为已覆盖(只标记一次)
for (int x = x1; x < x2; x++) {
for (int y = y1; y < y2; y++) {
covered[x][y] = true;
}
}
}
// 统计所有被覆盖的方格数量(即总面积)
int total = 0;
for (int x = 0; x < MAX; x++) {
for (int y = 0; y < MAX; y++) {
if (covered[x][y]) {
total++;
}
}
}
cout << total << endl;
return 0;
}蓝桥杯109 分考场
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
bool know[N][N]; // 标记两人是否认识,know[a][b]=true表示a和b认识
int room[N][N]; // 考场安排:room[i][j]表示第i个考场的第j个位置坐的人编号
int min_room = N; // 最少考场数,初始设为最大可能值n
int n, m;
// dfs:安排第x个人,当前已用room_num个考场
void dfs(int x, int room_num) {
// 剪枝:当前考场数已≥最优解,无需继续
if (room_num >= min_room) return;
// 所有人体安排完毕,更新最优解
if (x > n) {
min_room = room_num;
return;
}
// 尝试把第x个人安排到已有的每个考场
for (int i = 1; i <= room_num; i++) {
int j = 1;
// 找到考场i中第一个空位置(且该位置所有人都不认识x)
while (room[i][j] && !know[x][room[i][j]]) j++;
// 找到空位置,安排x入座
if (room[i][j] == 0) {
room[i][j] = x;
dfs(x + 1, room_num); // 安排下一个人
room[i][j] = 0; // 回溯:撤销安排
}
}
// 所有已有考场都坐不下,新开一个考场
room[room_num + 1][1] = x;
dfs(x + 1, room_num + 1);
room[room_num + 1][1] = 0; // 回溯:撤销新考场的安排
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
// 初始化人际关系表
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
know[a][b] = know[b][a] = true; // 互相认识
}
dfs(1, 1); // 从第1个人开始安排,初始1个考场
cout << min_room << '\n';
return 0;
}蓝桥杯110 合根植物
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1000010; // 最大格子数:1000*1000=1e6,开1e6+10足够
int parent[MAX]; // 记录每个格子的父节点(并查集核心)
// 查找x的根节点,带路径压缩(优化查找效率)
int find(int x) {
return parent[x]==x ? x : parent[x]=find(parent[x]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int m, n, k;
cin >> m >> n >> k;
int total = m * n; // 总格子数
// 初始化并查集:每个格子的父节点是自己
for (int i = 1; i <= total; ++i) {
parent[i] = i;
}
// 处理k次合根操作
for (int i = 0; i < k; ++i) {
int a, b;
cin >> a >> b;
int root_a = find(a); // 找a的根
int root_b = find(b); // 找b的根
if (root_a != root_b) { // 根不同则合并
parent[root_a] = root_b;
}
}
// 统计根节点数量(即合根植物总数)
int count = 0;
for (int i = 1; i <= total; ++i) {
if (parent[i] == i) { // 根节点的父节点是自己
count++;
}
}
cout << count << '\n';
return 0;
}Q:可以去掉ins.resize(n) 吗?
A:不可以。
如果删掉ins.resize(n),ins是一个空的vector<Interval>(size()=0),执行cin >> ins[i].a >> ins[i].b时,i从 0 到 n-1,而ins的有效下标范围是[0, size()-1](此时 size=0,无有效下标)
这会触发未定义行为(通常是程序崩溃、输出乱码,或运行时错误)
举个简单例子:
vector<Interval> ins; // 空vector,size=0
ins[0].a = 10; // 错误!下标0超出了空vector的范围蓝桥杯111 区间移位
每个区间 [a,b] 可以左右移动,但移动的最大距离不超过 k ,所以移动后区间的可能范围是 [a−k, b+k]。现在的问题是能不能用这些 “可伸缩的区间”,拼接出一个连续区间,覆盖 [0, 10000]?
这样就把移位问题变成了每个区间有一个可选的覆盖范围 [a−k, b+k],选一个具体位置让它们连起来覆盖目标。算法竞赛里,区间覆盖问题的最优解法就是贪心。
区间覆盖问题的贪心策略:
从左往右覆盖,每次选能接上当前覆盖终点、且能覆盖到最右边的区间。
为什么要这样?因为要尽可能把覆盖范围往右推,减少后续需要的区间数量,最快达到目标 10000。
在这个题里可以拆成两个动作:
找能衔接的区间:区间的可选范围 [a−k, b+k] 必须和当前已覆盖的 [0, cover] 有交集,也就是代码里的核心条件 a−k ≤ cover && b+k ≥ cover
选能推最远的区间:找到衔接区间后,要让 cover 尽可能变大,这就是代码里两种 cover 更新规则的来源(本质是计算这个区间能覆盖到的最右端)
(1)初始化:
复制原始区间到 temp,因为要删除用过的区间,避免修改原数据;
cover = 0 ,从起点 0 开始覆盖;
ok = false,标记本轮是否找到可用区间。
(2)循环找区间:
遍历 temp,找第一个满足衔接条件的区间(为什么是第一个?因为原区间已经按 b 升序排序,前面的区间右端点更小,不会影响后续选择)
找到后,计算这个区间能覆盖的最右端,对应两种 cover 更新情况:
a. 区间右移就能接上 cover,覆盖最右端是 cover + (b−a)(区间本身长度)
b. 区间需要左移才能接上 cover,覆盖最右端是 b + k(区间右移到极限的位置)
删除用过的区间,避免重复使用;
标记 ok = true,进入下一轮覆盖。
(3)终止条件:
要么 cover ≥ 10000,成功覆盖,返回 true;
要么找不到衔接区间,失败,返回 false。
#include <bits/stdc++.h>
using namespace std;
struct Interval { double a, b; };
vector<Interval> ins;
int n;
bool check(double k) {
vector<Interval> temp = ins;
double cover = 0;
while (true) {
bool ok = false;
for (int i = 0; i < temp.size(); i++) {
double a = temp[i].a, b = temp[i].b;
if (a - k <= cover && b + k >= cover) {
ok = true;
if (a + k >= cover) {
cover += (b-a);
} else {
cover = b + k;
}
temp.erase(temp.begin() + i);
break;
}
}
// 终止条件:要么覆盖到10000(成功),要么找不到能接的区间(失败)
if (cover >= 10000 || !ok) break;
}
return cover >= 10000;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
ins.resize(n);
for (int i = 0; i < n; i++) cin >> ins[i].a >> ins[i].b;
// 按右端点排序(贪心基础,不能省)
sort(ins.begin(), ins.end(), [](Interval x, Interval y) {
return x.b < y.b;
});
// 无脑枚举:步长0.5,从小到大试
for (double k = 0; k <= 10000; k += 0.5) {
if (check(k)) {
cout << k << '\n';
return 0;
}
}
return 0;
}temp.begin() 是迭代器(可以理解为 “指向容器第一个元素的指针”),不是数字 0;
vector 的 erase 函数只接受迭代器参数,不接受整数下标,所以 temp.erase(i) 会直接编译报错;
temp.begin() + i 的作用是:从 “第一个元素的迭代器” 往后偏移 i 步,得到 “指向第 i 个元素的迭代器”,这是 vector 删除指定下标元素的标准写法。
这个题也可以不使用结构体,如下修改:
vector<Interval> ins 改成 vector<pair<int, int>> ins
访问成员:a/b 改成 first/second
排序 lambda 的参数类型改为 pair
输入赋值改为 ins[i] = {a, b};
int n;
vector<pair<int, int>> ins; // 改成 pairint a = temp[i].first, b = temp[i].second; // 访问方式改为 first/second sort(ins.begin(), ins.end(), [](const pair<int, int>& x, const pair<int, int>& y) {
return x.second < y.second; // 按右端点排序
});
for (int i = 0; i < n; i++) {
double a, b;
cin >> a >> b;
ins[i] = {a, b}; // 赋值方式
}蓝桥杯113 填字母游戏
#include <bits/stdc++.h>
using namespace std;
// 记忆化缓存
unordered_map<string, int> memo;
int dfs(string s) {
// 先查缓存,有结果直接返回,避免重复计算
if (memo.find(s) != memo.end()) return memo[s];
// 有LOL,当前玩家输
if (s.find("LOL") != string::npos) return memo[s] = -1;
// 没空格,平局
if (s.find('*') == string::npos) return memo[s] = 0;
bool can_tie = false;
for (int i = 0; i < s.size(); ++i) {
if (s[i] == '*') {
// 试填L
s[i] = 'L';
int res = dfs(s);
s[i] = '*';
if (res == -1) return memo[s] = 1; // 对手输,我赢
if (res == 0) can_tie = true;
// 试填O
s[i] = 'O';
res = dfs(s);
s[i] = '*';
if (res == -1) return memo[s] = 1; // 对手输,我赢
if (res == 0) can_tie = true;
}
}
// 不能赢,判断能否平
return memo[s] = (can_tie ? 0 : -1);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
while (n--) {
string s;
cin >> s;
memo.clear();
cout << dfs(s) << '\n';
}
return 0;
}Q:为什么 int res = dfs(s); 这里的res代表的是对手的结果
A:代码中 int res = dfs(s);本质是我(当前玩家)走了一步棋(把 * 改成 L/O),生成了新的字符串 s,然后把这个新棋局交给对手,调用 dfs(s) 就是计算对手在这个新棋局下,用最优策略玩的最终结果
Q:为什么代码里只处理了 res == -1(对手输)和 res == 0(对手平局),没有显式处理 res == 1(对手赢)的情况?
A:代码的逻辑是遍历所有可能的走法,找对自己最有利的结果
res = dfs(s) 的返回值是对手在新棋局下的最优结果
res = -1:对手必输,我必赢(最优选择,直接返回 1)
res = 0:对手只能平局,我也能平局(标记 can_tie)
res = 1:对手必赢,我走这步会输(放弃这步,试其他走法)
如果某一步的 res == 1,说明我走这步后,对手必赢,这是对我最不利的选择,所以代码不会做任何操作。既不返回,也不标记,只是继续遍历下一个可填位置,看看有没有更好的走法(比如能赢或平局的)
Q:什么是记忆化?
A:记忆化(也叫缓存)是一种优化递归或动态规划算法的核心技巧,本质是:
把递归过程中已经计算过的状态结果存起来(用哈希表或数组),下次再遇到相同状态时,直接返回已存的结果,避免重复计算。
Q:memo[s] 属于谁?
A:memo[s] 既不专属对手,也不专属自己,而是专属 “状态 s” 的固定结果。memo[s] 存储的是当棋局处于状态 s 时,当前执棋的玩家在最优策略下的最终结果。memo[s] 只和棋局状态s 绑定,和 是你走还是对手走无关,谁处于状态 s 当当前玩家,memo[s] 就是谁的结果。
蓝桥杯117 碱基
第一步:枚举所有合法组合
题目要求选m个物种,最直接的办法就是用DFS/回溯枚举所有C(n,m)种组合。
第二步:对每个组合计算贡献
选好m个物种后,题目要统计“子串在所有选中物种里的出现次数乘积之和”。这里的小技巧是锚定第一个物种的子串,因为如果遍历所有可能的k长子串,范围太大,但第一个物种的k长子串数量是有限的,而且其他物种里的子串只有和它匹配才会有贡献,这样就缩小了枚举范围。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
int n, m, k; // n:物种数,m:选的数量,k:子串长度
vector<string> s; // 存储所有物种的DNA
vector<int> chosen; // 选中的m个物种下标
ll ans = 0;
vector<unordered_map<string, int>> sub_count; // 预处理每个字符串的k长子串计数
// 预处理函数,统计每个字符串的k长子串出现次数
void preprocess(int idx) {
const string& t = s[idx];
unordered_map<string, int> cnt;
int len = t.size();
for (int i = 0; i + k <= len; i++) {
string sub = t.substr(i, k);
cnt[sub]++;
}
sub_count.push_back(cnt);
}
// DFS选m个物种
void dfs(int idx) {
// 终止条件1:选够m个物种,计算该组合的贡献
if (chosen.size() == m) {
// 只处理第一个选中物种
int first_id = chosen[0];
for (auto& p : sub_count[first_id]) { // 遍历第一个物种的所有k长子串
string sub = p.first; // 取出子串
int cnt_first = p.second; // 取出第一个物种中该子串的次数
ll mul = cnt_first; // 第一个物种的次数
// 遍历剩余选中的物种
for (int i = 1; i < chosen.size(); i++) {
int id = chosen[i];
mul = mul * sub_count[id][sub] % MOD;
}
ans = (ans + mul) % MOD;
}
return;
}
// 终止条件2:遍历完所有物种,直接返回
if (idx >= n) return;
// 先试试不选第idx个物种
dfs(idx + 1); // 去处理下一个物种
// 再试试选第idx个物种
// 把第idx个物种加入选中列表
chosen.push_back(idx);
dfs(idx + 1); // 去处理下一个物种 写成dfs(idx)会重复处理当前物种
chosen.pop_back(); // 处理完后,把第idx个物种从选中列表删掉(恢复原样)
}
int main() {
cin >> n >> m >> k;
s.resize(n); // 新增:动态初始化vector大小,适配任意n
for (int i = 0; i < n; i++) {
cin >> s[i];
preprocess(i); // 调用预处理函数
}
dfs(0);
cout << ans % MOD << endl;
return 0;
}蓝桥杯118 机器人塔
#include <bits/stdc++.h>
using namespace std;
char tower[50][50]; // 储存塔
int M, N, layer;
long long ans = 0;
void buildTower(){
for(int i = layer; i >= 2; --i){
for(int j = 1; j < i; ++j){
if(tower[i][j] == tower[i][j+1])
tower[i-1][j] = 'A';
else
tower[i-1][j] = 'B';
}
}
}
bool checkCount(){
int cntA = 0, cntB = 0;
for(int i = 1; i <= layer; ++i){
for(int j = 1; j <= i; ++j){
if(tower[i][j] == 'A') cntA++;
else cntB++;
}
}
return cntA == M && cntB == N;
}
void dfs(int pos){
// pos 表示当前正在处理底层(第layer层)的第pos个格子
if(pos > layer){
buildTower();
if (checkCount()) ans++;
return;
}
// 情况1:当前位置填'A'
tower[layer][pos] = 'A';
dfs(pos + 1);
// 情况2:当前位置填'B'
tower[layer][pos] = 'B';
dfs(pos + 1);
}
int main(){
cin >> M >> N;
int sum = M + N;
layer = (sqrt(1 + 8 * sum) - 1) / 2;
dfs(1);
cout << ans << endl;
return 0;
}Q:layer = (sqrt(1 + 8 * sum) - 1) / 2;是怎么得到的?
塔的形状是金字塔形:第1层1个格子,第2层2个格子,第3层3个格子...
总共有 layer 层
总格子数 sum = M + N
金字塔的总格子数是一个等差数列的和 1 + 2 + 3 + ... + layer
等差数列求和公式 S = n × (a₁ + aₙ) ÷ 2
S = 总和(就是 sum)
n = 项数(就是 layer)
a₁ = 首项 = 1
aₙ = 末项 = layer
代入后 sum = layer × (1 + layer) ÷ 2
两边乘以2后 2 × sum = layer × (layer + 1)
展开后 layer² + layer - 2 × sum = 0
对于一元二次方程 ax² + bx + c = 0 x = [-b ± √(b² - 4ac)] ÷ (2a)
代入后 layer = [-1 ± √(1 + 8 × sum)] ÷ 2
因为层数必须是正数,所以取正号 layer = [√(1 + 8 × sum) - 1] ÷ 2
Q:为什么是i>=2以及j<i?
规则是根据第 i 层的两个相邻格子,推导第 i-1 层的一个格子
所以tower[i-1][j] 由 tower[i][j] 和 tower[i][j+1] 决定
i = layer:从最底层开始(第4层)
i >= 2:推导到第2层为止
注意数组是从[1][1]开始,而不是[0][0]开始的,这样的话第几层就有几个格子
【层数代表对应层格子数】
j = 1:从第1列开始
j < i:到第 i-1 列结束
为什么是 j < i 而不是 j <= i?
推导 tower[i-1][j] 需要 tower[i][j] 和 tower[i][j+1]
当 j = i 时:
需要 tower[i][i] 和 tower[i][i+1]
但 tower[i][i+1] 不存在(越界了)
Q:为什么后面又 j<=i
因为用途不同,前者目的是根据已知的第i层,推导第i-1层
条件是j < i ,因为需要 tower[i][j+1],不能越界,函数逻辑是自底向上
后者目的是遍历金字塔的所有格子进行统计
条件是j <= i ,因为第i层有i个格子
if(pos > layer){ // 底层填满了
// 处理这个完整解
return; // 这个解处理完了,返回上一层
}
Q: 为什么不可以去掉 if (checkCount()) ?
底层:A A A
推导的塔:
A
A A
A A A
统计:A=6, B=0 不符合要求,但错误代码会计数
蓝桥杯121 压缩变换
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N]; // 储存原序列
int c[N]; // 标记最后一次出现
int main(){
int n;
cin >> n;
for(int i = 1; i <= n; ++i){
cin >> a[i];
// 判断当前数字是否首次出现(暴力遍历)
bool is_first = true;
int last_pos = 0;
for(int j = 1; j < i; ++j){
if(a[j] == a[i]){
is_first = false;
last_pos = j; // 更新目前整数在它之前的最后一次出现的相同整数的位置
}
}
if(is_first){ // 首次出现
cout << -a[i] << " ";
c[i] = 1;
} else { // 重复出现
int cnt = 0;
for(int j = last_pos + 1; j < i; ++j) cnt += c[j];
cout << cnt << " ";
c[last_pos] = 0; // 因为目前整数为新的最后一次 故旧最后一次置0
c[i] = 1; // 新最后一次置1
}
}
return 0;
}c[i]=1表示位置i是某数字的最后一次出现,0表示不是
蓝桥杯123 取球博弈
#include <iostream>
using namespace std;
char dp[1005][2][2] = {0}; // 储存的是先手的结果
int take[3];
char dfs(int sum, int f, int s){
if(dp[sum][f][s]) return dp[sum][f][s]; // 记忆化
// for循环判断是否终止 无法取球则终止
bool can_take = false;
for(int i = 0; i < 3; ++i){
if(sum >= take[i]){
can_take = true;
break;
}
}
// 上面的for循环没进去说明球被取完 终止 胜负判断
if(!can_take){
if((f%2) == (s%2)) return dp[sum][f][s] = '0'; // 奇偶相同 平局
// 先手为奇数 赢 先手为偶数 输
return dp[sum][f][s] = (f%2 == 1) ? '+' : '-';
}
char res = '-'; // 初始化结果为先手必败
// 尝试所有可能结果
for(int i = 0; i < 3; ++i){
if(sum >= take[i]){
// 先手取球 更新奇偶性
int new_f = (f + take[i]) % 2;
// 先手取球完成 开始后手取球 先后手互换
char opp = dfs(sum - take[i], s, new_f);
// 对手必败 先手胜
if(opp == '-') return dp[sum][f][s] = '+';
// 双方平局
if(opp == '0') res = '0'; // 不直接返回是因为后面可能有胜利走法
}
}
return dp[sum][f][s] = res;
}
int main(){
cin >> take[0] >> take[1] >> take[2];
for(int i = 0; i < 5; ++i){
int n;
cin >> n;
cout << dfs(n, 0, 0) << " ";
}
return 0;
}先思考需要记录什么状态?
1. 剩余球数 sum
2. 当前先手的奇偶性
3. 当前后手的奇偶性
胜负只与奇偶有关,所以用0/1表示
char dp[1005][2][2] = {0}; // 这是最先确定的
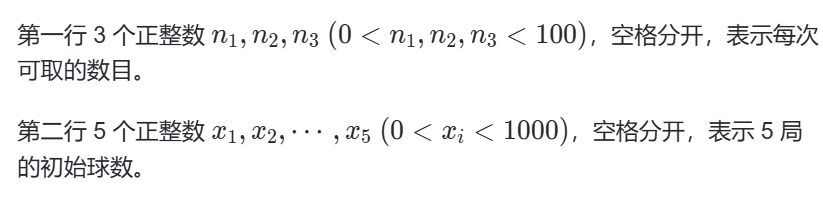
蓝桥杯126 交换瓶子
#include <iostream>
using namespace std;
const int N = 1e4 + 5;
int a[N]; // 存储瓶子排列
int main() {
int n, ans = 0;
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
}
for (int i = 1; i <= n; ++i) { // 题目中下标从1开始
while (a[i] != i) {
swap(a[i], a[a[i]]); // 把当前瓶子交换到它该在的位置
ans++;
}
}
cout << ans << endl;
return 0;
}
DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)