基于人工势场法的 动态路径规划+曲线平滑处理 路径规划算法 地图好修改 自己研究编写的Matlab路径规划 可自行设置起始点，目标点，障碍物，自由更换地图。 ——————————————————— 可以和A*和RRT融合 动态障碍物 预先声明：该程序为版权所述，仅供学习参考使用。

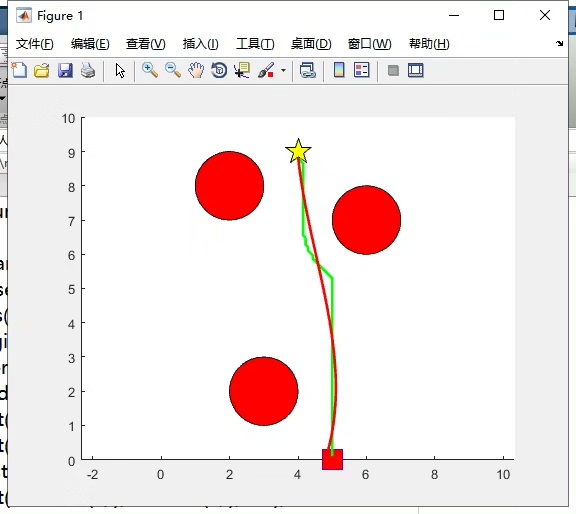
在机器人运动规划领域，路径规划是一个关键问题。今天要分享的是基于人工势场法，并结合曲线平滑处理的路径规划方案，而且这个方案可以自由修改地图，还能和 A*、RRT 等算法融合应对动态障碍物哦，这一切都是我自己研究编写的 Matlab 路径规划程序~

人工势场法基础

人工势场法的核心思想，就是将机器人在环境中的运动，看作是在一个虚拟的势场中运动。目标点产生引力势场，吸引机器人靠近；障碍物产生斥力势场，排斥机器人远离。

以下是简单的引力势场函数代码示例（Matlab）：

function Ug = attractive_potential(robot, goal, eta)
    % robot 是机器人当前位置，goal 是目标点位置，eta 是引力系数
    dist = norm(robot - goal);
    Ug = 0.5 * eta * dist^2;
end

这段代码计算了机器人在引力势场中的势能。通过 norm 函数计算机器人到目标点的欧几里得距离 dist，然后根据引力势场公式 $U_g = \frac{1}{2}\eta d^2$（其中 $\eta$ 是引力系数，$d$ 是距离），算出引力势能 Ug。

基于人工势场法的 动态路径规划+曲线平滑处理 路径规划算法 地图好修改 自己研究编写的Matlab路径规划 可自行设置起始点，目标点，障碍物，自由更换地图。 ——————————————————— 可以和A*和RRT融合 动态障碍物 预先声明：该程序为版权所述，仅供学习参考使用。

斥力势场函数代码如下：

function Ur = repulsive_potential(robot, obstacle, rho0, xi)
    % robot 是机器人当前位置，obstacle 是障碍物位置，rho0 是影响距离，xi 是斥力系数
    dist = norm(robot - obstacle);
    if dist <= rho0
        Ur = 0.5 * xi * (1/dist - 1/rho0)^2;
    else
        Ur = 0;
    end
end

这里，先计算机器人到障碍物的距离 dist。当距离小于等于影响距离 rho0 时，按照斥力势场公式 $Ur = \frac{1}{2}\xi (\frac{1}{d} - \frac{1}{\rho0})^2$ 计算斥力势能 Ur；当距离大于 rho0 时，斥力势能为 0，即障碍物在这个距离外对机器人没有斥力影响。

动态路径规划

结合引力和斥力势场，就可以得到总的势场，进而规划出动态路径。

function [path] = dynamic_path_planning(robot_start, goal, obstacles, eta, xi, rho0)
    path = [robot_start];
    robot = robot_start;
    while norm(robot - goal) > 0.1 % 设定一个接近目标的阈值
        Ug_grad = eta * (robot - goal);
        Ur_grad = zeros(2,1);
        for i = 1:size(obstacles, 1)
            obstacle = obstacles(i,:);
            dist = norm(robot - obstacle);
            if dist <= rho0
                Ur_grad = Ur_grad + xi * (1/dist - 1/rho0) * (1/dist^3) * (robot - obstacle);
            end
        end
        total_grad = Ug_grad + Ur_grad;
        robot = robot - 0.01 * total_grad; % 步长设为 0.01
        path = [path; robot];
    end
end

在这个函数里，从起始点 robotstart 开始，不断计算引力梯度 Uggrad 和斥力梯度 Urgrad，累加得到总的梯度 totalgrad。机器人沿着负梯度方向移动一小步（步长 0.01），并记录路径点，直到机器人接近目标点（距离小于 0.1）。

曲线平滑处理

路径规划出来后，可能比较曲折，需要进行曲线平滑处理。这里简单使用样条插值法。

function smooth_path = smooth_path(path, num_points)
    x = path(:,1);
    y = path(:,2);
    t = 1:size(path, 1);
    new_t = linspace(1, size(path, 1), num_points);
    new_x = spline(t, x, new_t);
    new_y = spline(t, y, new_t);
    smooth_path = [new_x, new_y];
end

这段代码先提取路径点的 x 和 y 坐标，然后利用 linspace 函数生成新的插值点位置 newt，再通过 spline 函数进行样条插值，得到平滑后的 x 和 y 坐标，组合成平滑路径 smoothpath。

地图修改与参数设置

这个路径规划程序的一大优势就是地图好修改。可以自行设置起始点、目标点、障碍物，自由更换地图。比如设置起始点为 [0, 0]，目标点为 [10, 10]，障碍物为 [[2, 2]; [5, 5]; [8, 8]]：

robot_start = [0, 0];
goal = [10, 10];
obstacles = [[2, 2]; [5, 5]; [8, 8]];
eta = 1; % 引力系数
xi = 100; % 斥力系数
rho0 = 1; % 障碍物影响距离

这样就轻松完成了地图和参数设置。

与 A* 和 RRT 融合

理论上，将人工势场法与 A、RRT 融合可以更好地应对复杂动态环境。比如在 A 算法搜索到大致路径后，利用人工势场法对局部路径进行优化，处理动态障碍物。虽然具体实现代码较复杂，但思路就是结合不同算法的优势。

% 简单示意如何在 A* 基础上调用人工势场法优化
% 假设 A* 算法得到路径 astar_path
astar_path = a_star_planning(robot_start, goal, obstacles);
optimized_path = dynamic_path_planning(astar_path(1,:), goal, obstacles, eta, xi, rho0);

这里先调用 A 算法得到 astar_path，然后把 A 路径的起始点作为人工势场法动态路径规划的起始点，进一步优化路径，以应对动态障碍物。

预先声明：该程序为版权所述，仅供学习参考使用。希望这个分享能对大家在路径规划研究上有所帮助，欢迎一起交流探讨呀~