RRT 3D， RRT星 3D 路径规划算法，机器人路径规划导航RRTstar，有算法matlab源文件，可直接运行并且有中文注释，适合初学者学习入门。 算法，matlab源代码学习。

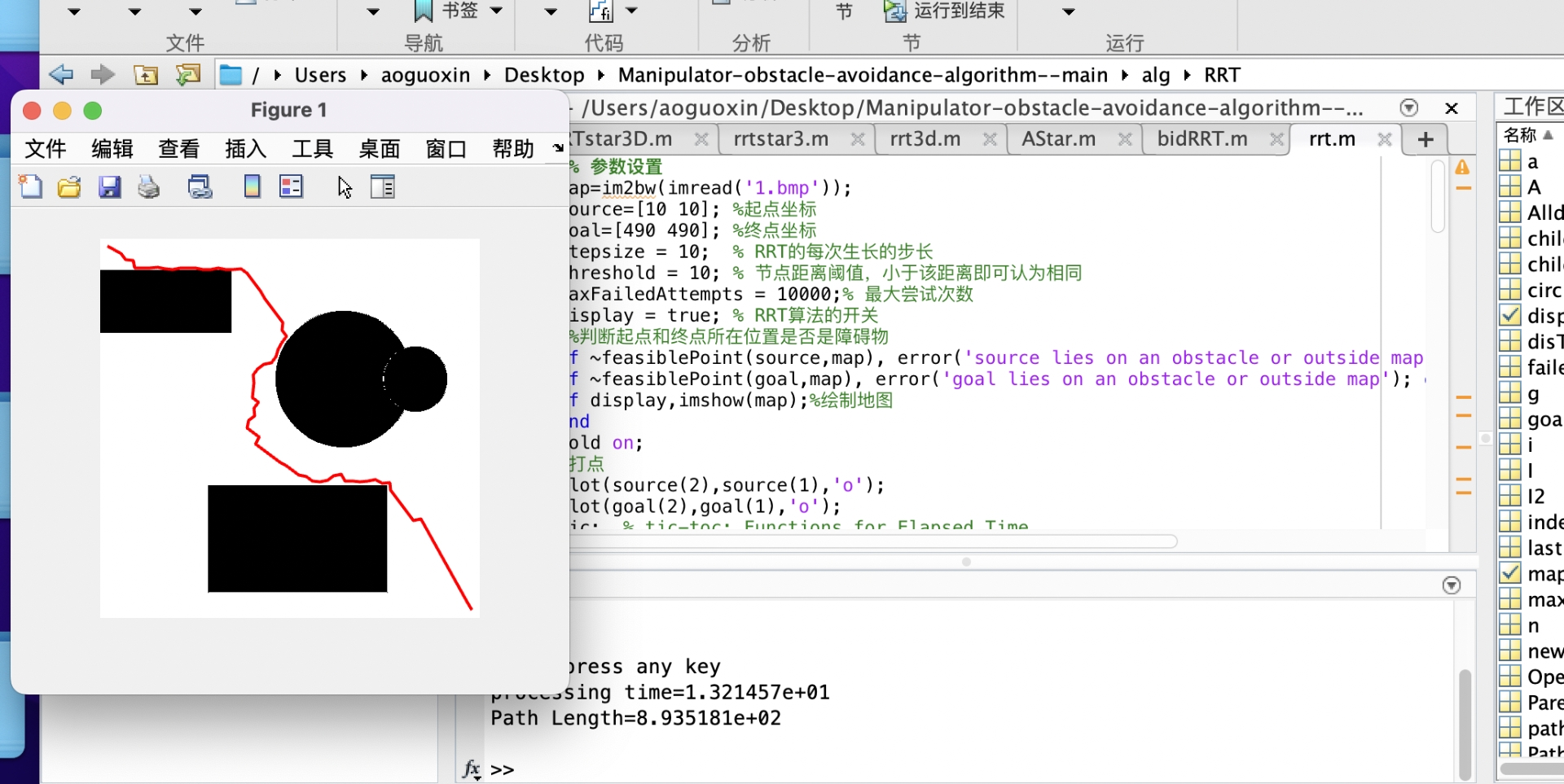
在机器人路径规划导航的领域里，RRT（快速探索随机树）及其优化版本 RRT（RRT 星）算法就像是指引机器人在复杂空间中穿梭的智慧灯塔。今天咱们就深入到 3D 空间，一起揭开 RRT 3D 和 RRT 3D 路径规划算法的神秘面纱，并且借助 MATLAB 源代码来更好地理解它们，特别适合刚入门这个领域的小伙伴们哦。

一、RRT 3D 算法初窥

RRT 算法的核心思想是通过在搜索空间中随机采样点，逐步构建一棵搜索树，从起始点不断向目标点生长，直到树的节点能够覆盖目标点，此时就找到了一条路径。在 3D 环境下，它要处理的是三维空间中的位置信息，复杂度自然比二维空间有所提升。

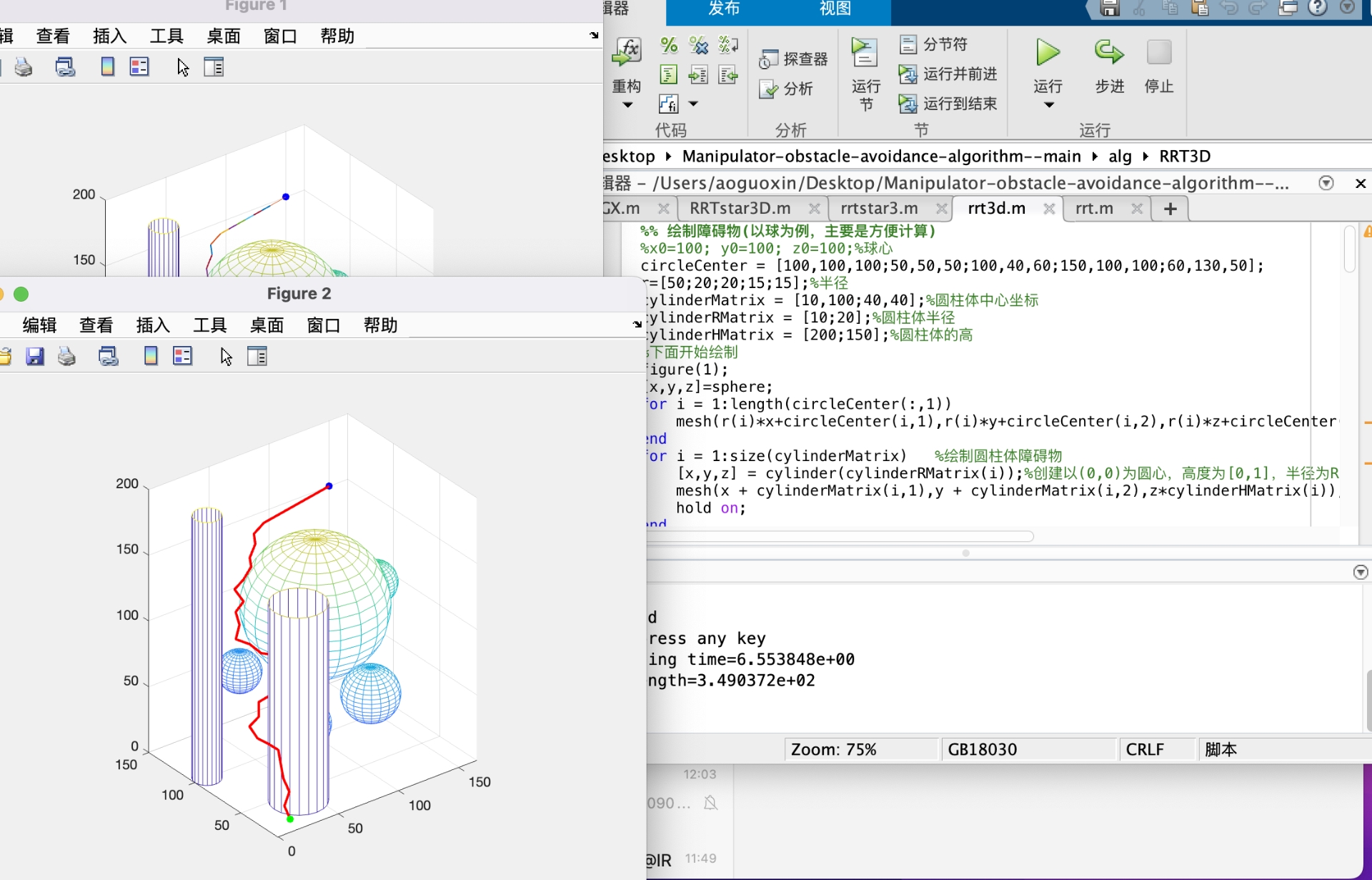
RRT 3D， RRT星 3D 路径规划算法，机器人路径规划导航RRTstar，有算法matlab源文件，可直接运行并且有中文注释，适合初学者学习入门。 算法，matlab源代码学习。

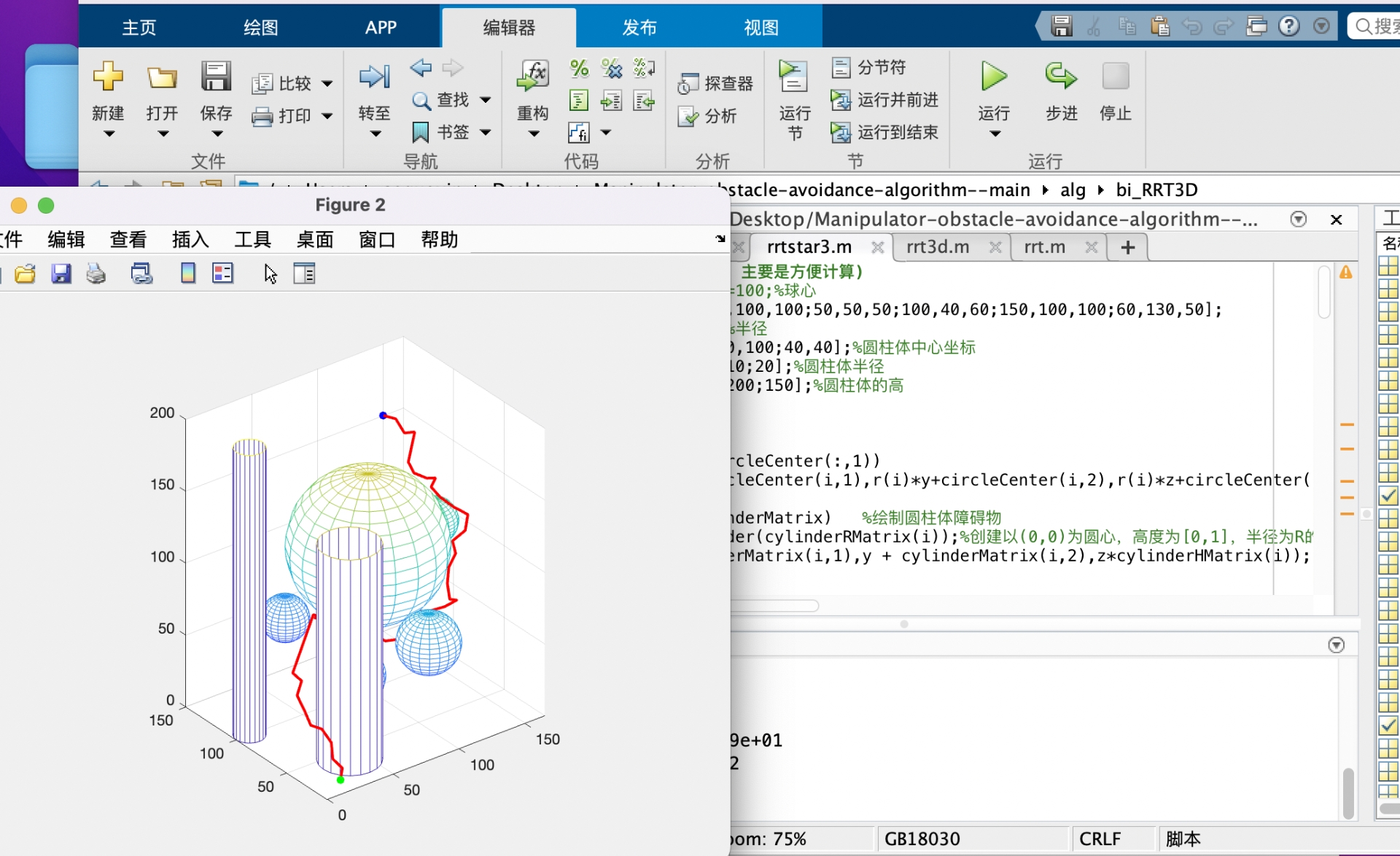
假设我们有一个简单的 3D 环境，包含一些障碍物，咱们来看看 RRT 3D 算法的 MATLAB 代码实现片段：

% 初始化参数
start = [0, 0, 0]; % 起始点坐标
goal = [10, 10, 10]; % 目标点坐标
obstacles = [5, 5, 5, 2]; % 障碍物信息，这里表示中心坐标为(5,5,5)，半径为2
step_size = 1; % 每次扩展的步长
max_iter = 1000; % 最大迭代次数

% 初始化树
tree = struct('parent', [], 'node', start);

这段代码里，我们首先定义了起始点 start、目标点 goal、障碍物信息 obstacles 以及一些算法参数，像每次扩展的步长 stepsize 和最大迭代次数 maxiter。然后初始化了一个树结构 tree，这个树会在后续不断生长，记录路径搜索的过程。

for iter = 1:max_iter
    % 随机采样一个点
    rand_point = [rand() * 10, rand() * 10, rand() * 10];
    % 找到树中距离随机点最近的节点
    [~, nearest_index] = min(sum(([tree.node] - repmat(rand_point, size([tree.node], 2), 1)).^2, 1));
    nearest_node = tree.node(:, nearest_index);
    % 朝着随机点扩展一步
    new_node = nearest_node + step_size * (rand_point - nearest_node) / norm(rand_point - nearest_node);
    % 检查新节点是否在障碍物内
    if norm(new_node - obstacles(1:3)) > obstacles(4)
        % 将新节点添加到树中
        new_index = length(tree.node) + 1;
        tree.parent(new_index) = nearest_index;
        tree.node(:, new_index) = new_node;
        % 检查是否到达目标点附近
        if norm(new_node - goal) < step_size
            break;
        end
    end
end

在这个循环里，每次迭代首先随机采样一个点 randpoint，然后在已有的树 tree 中找到距离这个随机点最近的节点 nearestnode。接着朝着随机点的方向扩展一步得到 newnode，这里通过步长 stepsize 来控制扩展的距离。之后检查新节点是否在障碍物内，如果不在，就把新节点添加到树里。同时，如果新节点已经足够接近目标点（距离小于步长），那就说明找到了路径，可以结束循环啦。

二、RRT* 3D 算法进阶

RRT 算法在 RRT 的基础上进行了优化，它不仅考虑找到一条可行路径，还致力于找到最优路径。RRT 在构建树的过程中，会对已有的路径进行重新评估和优化，使得路径的成本不断降低。

同样来看一段 RRT* 3D 的 MATLAB 代码片段：

% 初始化参数（和RRT部分类似，但增加了一些用于优化的参数）
start = [0, 0, 0];
goal = [10, 10, 10];
obstacles = [5, 5, 5, 2];
step_size = 1;
max_iter = 1000;
rewire_radius = 2; % 重连半径

% 初始化树
tree = struct('parent', [], 'node', start, 'cost', 0);

这里除了之前 RRT 算法的那些参数，新增了一个 rewire_radius，也就是重连半径，用于控制重连操作的范围。树结构 tree 里也增加了一个记录节点成本的 cost 字段。

for iter = 1:max_iter
    % 随机采样一个点
    rand_point = [rand() * 10, rand() * 10, rand() * 10];
    % 找到树中距离随机点最近的节点
    [~, nearest_index] = min(sum(([tree.node] - repmat(rand_point, size([tree.node], 2), 1)).^2, 1));
    nearest_node = tree.node(:, nearest_index);
    % 朝着随机点扩展一步
    new_node = nearest_node + step_size * (rand_point - nearest_node) / norm(rand_point - nearest_node);
    % 检查新节点是否在障碍物内
    if norm(new_node - obstacles(1:3)) > obstacles(4)
        % 找到在重连半径内的所有节点
        nearby_indices = find(sum(([tree.node] - repmat(new_node, size([tree.node], 2), 1)).^2, 1) < rewire_radius^2);
        new_cost = tree.cost(nearest_index) + norm(new_node - nearest_node);
        best_parent_index = nearest_index;
        % 寻找使新节点成本最小的父节点
        for i = nearby_indices
            if tree.cost(i) + norm(new_node - tree.node(:, i)) < new_cost
                new_cost = tree.cost(i) + norm(new_node - tree.node(:, i));
                best_parent_index = i;
            end
        end
        % 将新节点添加到树中
        new_index = length(tree.node) + 1;
        tree.parent(new_index) = best_parent_index;
        tree.node(:, new_index) = new_node;
        tree.cost(new_index) = new_cost;
        % 对重连半径内的节点进行重连优化
        for i = nearby_indices
            if i ~= new_index && tree.cost(new_index) + norm(tree.node(:, i) - new_node) < tree.cost(i)
                tree.parent(i) = new_index;
                tree.cost(i) = tree.cost(new_index) + norm(tree.node(:, i) - new_node);
            end
        end
        % 检查是否到达目标点附近
        if norm(new_node - goal) < step_size
            break;
        end
    end
end

这段代码和 RRT 的实现有不少相似之处，但在新节点加入树的过程中多了很多优化操作。首先找到重连半径内的所有节点 nearbyindices，然后寻找使新节点成本最小的父节点 bestparent_index，这一步是为了让新节点以最优的方式加入树，降低整体路径成本。之后不仅添加新节点，还对重连半径内的节点进行重连优化，看看是否可以通过以新节点为父节点来降低这些节点的成本。同样，当新节点接近目标点时结束循环。

三、总结与展望

RRT 3D 和 RRT 3D 算法为机器人在 3D 空间中的路径规划提供了强大的工具。RRT 算法简单直接，能够快速找到一条可行路径，而 RRT 算法则在此基础上进一步优化，努力为我们带来最优路径。通过 MATLAB 代码的实践，相信大家对这两个算法的理解会更加深刻。小伙伴们可以根据实际需求对这些代码进行调整和扩展，比如应用到更复杂的 3D 场景，或者尝试不同的参数设置来观察算法效果。希望大家在机器人路径规划的学习道路上越走越远，创造出更多有趣的应用！