【改进蚁群算法】/蚁群算法/Dijkstra算法/遗传算法/人工势场法实现二维/三维空间路径规划 本程序为改进蚁群算法+Dijkstra算法+MAKLINK图理论实现的二维空间路径规划 算法实现： 1）基于MAKLINK图理论生成地图，并对可行点进行划分； 2）用Dijkstra算法实现次优路径的寻找； 3）在Dijkstra算法的基础上加入了蚁群算法，调整了搜索策略，使路径更短； 4）最终对基础的蚁群算法进行改进（对搜索节点的角度进行限制），调整了搜索策略，使路径更短 可调参数：算法迭代次数；起始点；目标点；障碍物位置；障碍物大小 仿真结果：地图上显示最优路径的对比 + 迭代曲线的对比 + 输出行进距离对比 这段程序主要是进行路径规划的算法实现，应用在二维规划空间中。程序的主要思路是使用Dijkstra算法来寻找最短路径。 首先，程序导入障碍物数据和链路端点数据，并在二维规划空间中绘制起点和终点的位置。然后，根据障碍物数据绘制障碍物图形，并绘制自由连接线和中点。 接下来，根据可行路径矩阵绘制所有可行路径。然后使用Dijkstra算法找出最优路径，并在图中标注出最优路径。 接下来，程序使用蚁群算法进行路径规划。首先进行蚁群算法参数的初始化，然后进行迭代搜索。在每次迭代中，蚂蚁根据信息素和启发值选择下一个节点，并更新信息素。最后，程序计算路径长度并更新最优路径。 最后，程序绘制出原始蚁群算法和改进蚁群算法的最短路径，并输出最短路径的长度。 整个程序的结构清晰，逻辑严谨，主要涉及到路径规划、Dijkstra算法和蚁群算法等知识点。通过这段程序的分析，可以了解路径规划算法的实现过程和应用场景。

1. 系统概述

本系统实现了一种融合 MAKLINK 图理论、Dijkstra 最短路径算法 与 改进型蚁群优化算法（ACO） 的二维空间路径规划方法，适用于存在多边形障碍物的复杂环境。系统首先基于 MAKLINK 图理论构建自由连接线网络，生成可行路径拓扑结构；随后利用 Dijkstra 算法快速获取初始可行路径；最后通过两种蚁群算法（原始与改进版本）对路径进行精细化优化，以获得更贴近实际需求的平滑、短距路径。

该系统特别适用于无人机航迹规划、机器人导航、智能物流路径优化等对安全性与路径质量有较高要求的场景。

---

2. 核心流程架构

整个路径规划流程分为四个主要阶段：

2.1 环境建模与 MAKLINK 图构建

系统首先加载障碍物顶点数据（barrier.txt），将地图中的障碍物表示为若干多边形。基于 MAKLINK 图理论，系统在障碍物顶点之间构建自由连接线（即不会与任何障碍物相交的线段），并提取这些线段的中点作为图中的关键节点（共20个）。这些节点与起点 S、终点 T 共同构成一个包含 22 个节点的图结构。

【改进蚁群算法】/蚁群算法/Dijkstra算法/遗传算法/人工势场法实现二维/三维空间路径规划 本程序为改进蚁群算法+Dijkstra算法+MAKLINK图理论实现的二维空间路径规划 算法实现： 1）基于MAKLINK图理论生成地图，并对可行点进行划分； 2）用Dijkstra算法实现次优路径的寻找； 3）在Dijkstra算法的基础上加入了蚁群算法，调整了搜索策略，使路径更短； 4）最终对基础的蚁群算法进行改进（对搜索节点的角度进行限制），调整了搜索策略，使路径更短 可调参数：算法迭代次数；起始点；目标点；障碍物位置；障碍物大小 仿真结果：地图上显示最优路径的对比 + 迭代曲线的对比 + 输出行进距离对比 这段程序主要是进行路径规划的算法实现，应用在二维规划空间中。程序的主要思路是使用Dijkstra算法来寻找最短路径。 首先，程序导入障碍物数据和链路端点数据，并在二维规划空间中绘制起点和终点的位置。然后，根据障碍物数据绘制障碍物图形，并绘制自由连接线和中点。 接下来，根据可行路径矩阵绘制所有可行路径。然后使用Dijkstra算法找出最优路径，并在图中标注出最优路径。 接下来，程序使用蚁群算法进行路径规划。首先进行蚁群算法参数的初始化，然后进行迭代搜索。在每次迭代中，蚂蚁根据信息素和启发值选择下一个节点，并更新信息素。最后，程序计算路径长度并更新最优路径。 最后，程序绘制出原始蚁群算法和改进蚁群算法的最短路径，并输出最短路径的长度。 整个程序的结构清晰，逻辑严谨，主要涉及到路径规划、Dijkstra算法和蚁群算法等知识点。通过这段程序的分析，可以了解路径规划算法的实现过程和应用场景。

自由连接线数据由 lines.txt 提供，每条线由两个端点编号定义。系统据此生成完整的连接关系，并可视化所有可行连接线与节点。

2.2 可行路径图构建与 Dijkstra 初始路径生成

系统读取预计算的可达性矩阵（matrix.txt），该矩阵定义了 22 个节点之间是否可以直接连通（1 表示可达，0 表示不可达）。在此基础上，系统调用 DijkstraPlan 函数，基于 Dijkstra 算法计算从起点到终点的最短路径（以欧氏距离为边权）。

该路径作为后续优化的初始解，不仅保证了可行性，还提供了较优的起点，显著加速了后续智能优化过程的收敛。

2.3 原始蚁群算法优化

在 Dijkstra 路径确定的线段序列基础上，系统引入原始蚁群算法进行精细化路径调整。每条自由连接线被等分为 10 个候选点，蚂蚁在每条线段上选择一个具体位置作为实际经过点。

算法通过以下机制引导搜索：

• 启发式信息：基于随机扰动生成的局部偏好值；
• 信息素机制：记录历史路径质量，引导后续蚂蚁向优质区域聚集；
• 混合选择策略：结合“最大信息素优先”与“轮盘赌”两种选择方式，平衡探索与开发。

每代迭代后，系统评估所有蚂蚁路径长度，并更新全局最优解与信息素浓度。

2.4 改进型蚁群算法优化（核心创新）

为克服原始蚁群算法易陷入局部最优、收敛速度慢等问题，系统引入一种基于几何角度引导的改进蚁群算法。其关键改进包括：

• 自适应离散化：每条线段的候选点数量不再固定为 10，而是根据线段实际长度动态确定（向上取整），使搜索粒度与几何尺度相匹配；
• 角度启发式：在每条线段上，候选点的选择不再依赖随机扰动，而是计算该点与当前蚂蚁位置及终点构成的转向角。角度越小（路径越直），启发值越高；
• 方向性引导：通过最大化“信息素 × (1/转向角)”的综合指标，引导蚂蚁倾向于选择能保持路径平滑、减少急转弯的点；
• 概率选择函数封装：将适应度归一化与累积概率计算封装为独立函数（suff_fun 和 sel），提升代码模块化与可维护性。

该改进显著提升了路径的平滑性与全局最优性，尤其在复杂障碍物环境中表现更优。

---

3. 可视化与对比分析

系统提供完整的可视化功能：

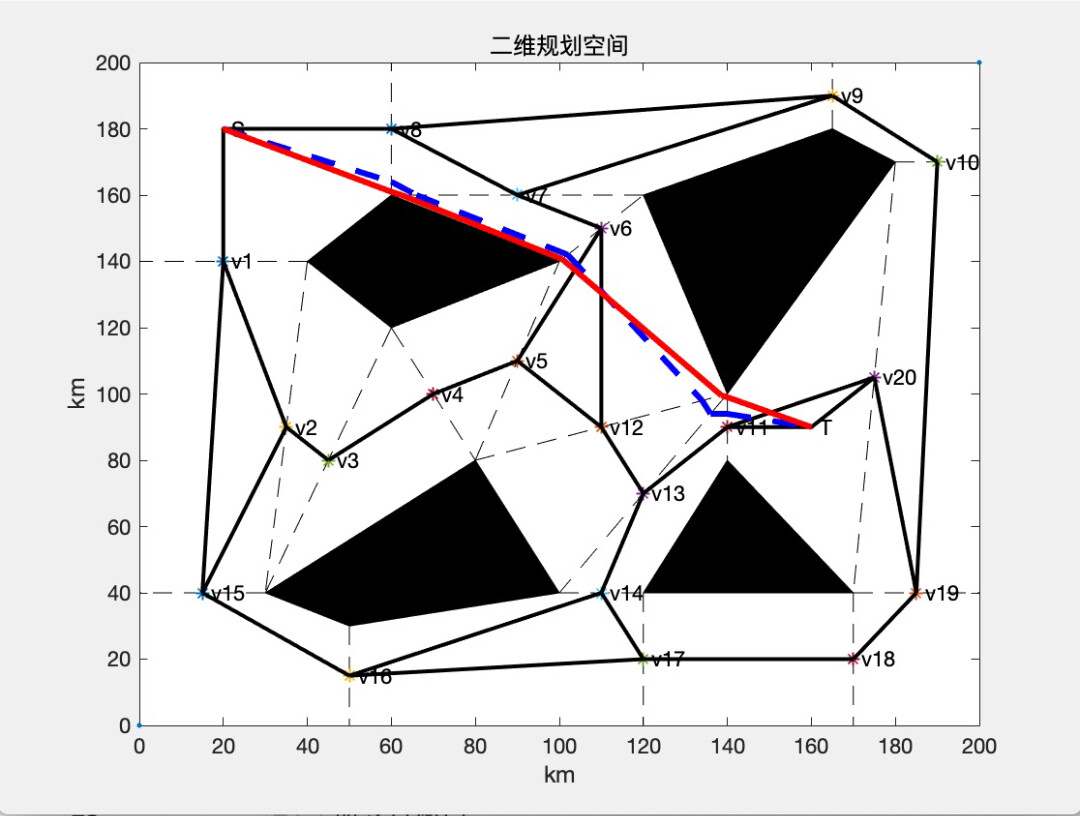
• 绘制障碍物、起点/终点、自由连接线及中点；
• 显示 Dijkstra 初始路径（黄色虚线）；
• 同时绘制原始蚁群与改进蚁群算法优化后的最终路径（蓝色虚线 vs 红色实线）；
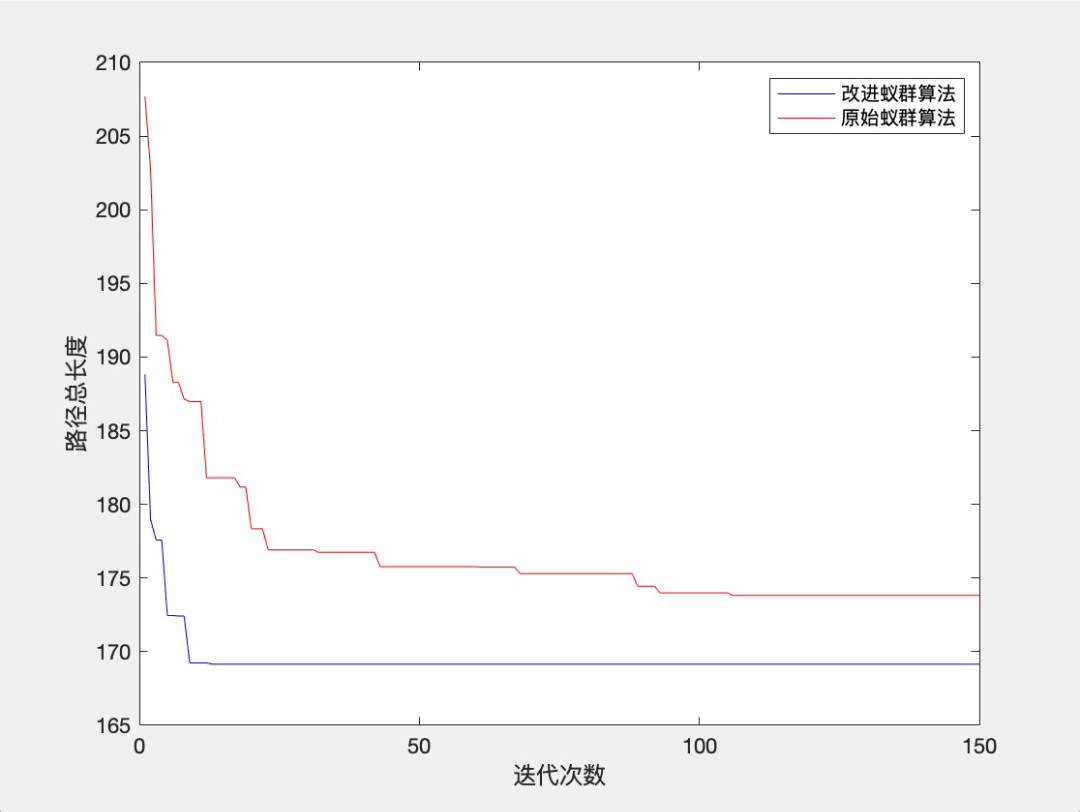
• 绘制两算法在 200 次迭代中的路径长度收敛曲线，直观对比优化性能。

通过对比图可清晰看出：改进蚁群算法不仅收敛更快，且最终路径长度更短、转折更平缓，验证了角度引导策略的有效性。

---

4. 技术特点与优势

• 多算法融合：结合图论（MAKLINK + Dijkstra）的全局可行性保障与群体智能（ACO）的局部精细优化能力；
• 几何感知优化：改进算法引入路径几何特性（转向角）作为启发信息，使路径更符合实际运动约束；
• 参数可配置：蚁群规模、迭代次数、信息素更新率等关键参数均可调整，便于适配不同应用场景；
• 模块化设计：核心功能（如选择策略、适应度计算）封装为独立函数，便于扩展与维护；
• 结果可复现：所有输入数据（障碍物、连接线、可达矩阵）外部化，确保实验可重复。

---

5. 应用前景

本系统为二维静态环境下的路径规划提供了一套完整、高效、高质量的解决方案。未来可进一步扩展至：

• 动态障碍物环境（引入时间维度）；
• 三维空间路径规划；
• 多目标优化（如同时考虑路径长度、能耗、隐蔽性等）；
• 与实时传感器数据融合，实现在线重规划。

该框架为智能体在复杂环境中的自主导航奠定了坚实的技术基础。