基于Matlab的改进人工势场法路径规划探究
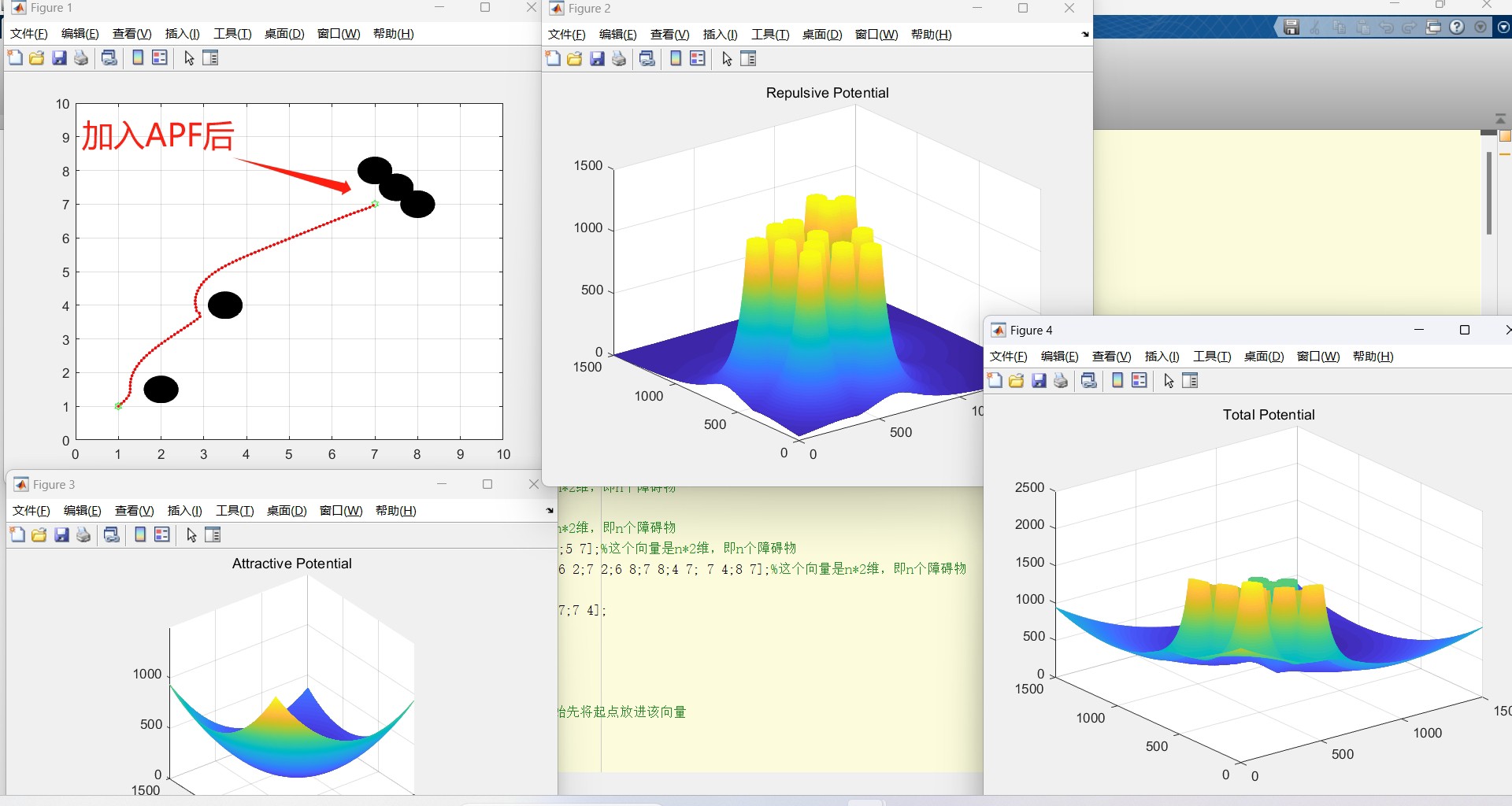
基于matlab实现改进的人工势场法,apf算法进行路径规划,通过改进斥力函数和引入模拟退火算法,克服局部极小值和目标不可达问题。并附送未改进的apf算法,可做改进与未改进的效果比对使用,如图,未改进的算法会陷入局部极小值从而导致路径规划失败。起始点位置,障碍物位置可以根据自己需求随便设置更改,自己设置地图进行路径规划,可自动生成斥力场,引力场,合力场。在机器人路径规划领域,人工势场法(APF)是
基于matlab实现改进的人工势场法,apf算法进行路径规划,通过改进斥力函数和引入模拟退火算法,克服局部极小值和目标不可达问题。 并附送未改进的apf算法,可做改进与未改进的效果比对使用,如图,未改进的算法会陷入局部极小值从而导致路径规划失败。 起始点位置,障碍物位置可以根据自己需求随便设置更改,自己设置地图进行路径规划,可自动生成斥力场,引力场,合力场。

在机器人路径规划领域,人工势场法(APF)是一种经典且应用广泛的方法。然而,传统的APF算法存在一些局限性,比如容易陷入局部极小值,导致目标不可达。今天咱们就来聊聊基于Matlab实现改进的APF算法,通过改进斥力函数和引入模拟退火算法来克服这些问题,同时也分享下未改进的APF算法,方便大家做效果比对。
未改进的APF算法
先来看未改进的APF算法实现。在Matlab里,我们首先要设定起始点、目标点还有障碍物的位置,这里咱们就根据需求随意设置一下。
% 定义起始点、目标点和障碍物位置
start = [0, 0];
goal = [10, 10];
obstacles = [2, 2; 4, 4; 6, 6];这段代码很简单,就是分别定义了起始点 start、目标点 goal 以及障碍物位置 obstacles,这里障碍物我们设置了三个点。
接下来是计算引力场和斥力场。引力场相对简单,引力与机器人到目标点的距离成正比。
% 计算引力
function F_att = compute_attractive_force(robot, goal, eta)
F_att = eta * (goal - robot);
end这个 computeattractiveforce 函数里,eta 是引力系数,通过它来调整引力的大小,引力向量就是目标点减去机器人当前位置再乘以引力系数。
斥力场计算稍微复杂点,当机器人靠近障碍物时斥力急剧增大。
% 计算斥力
function F_rep = compute_repulsive_force(robot, obstacles, rho0, k)
F_rep = [0, 0];
for i = 1:size(obstacles, 1)
dist = norm(robot - obstacles(i, :));
if dist < rho0
F_rep = F_rep + k * (1/dist - 1/rho0) * (1/dist^2) * (robot - obstacles(i, :));
end
end
end在 computerepulsiveforce 函数中,rho0 是一个距离阈值,当机器人与障碍物的距离 dist 小于 rho0 时,斥力开始起作用,k 是斥力系数。从代码里能看到,距离障碍物越近,斥力越大,方向是远离障碍物。
最后就是计算合力,规划路径了。
% 计算合力并规划路径
step_size = 0.1;
robot = start;
path = robot;
while norm(robot - goal) > step_size
F_att = compute_attractive_force(robot, goal, eta);
F_rep = compute_repulsive_force(robot, obstacles, rho0, k);
F_total = F_att + F_rep;
robot = robot + step_size * F_total / norm(F_total);
path = [path; robot];
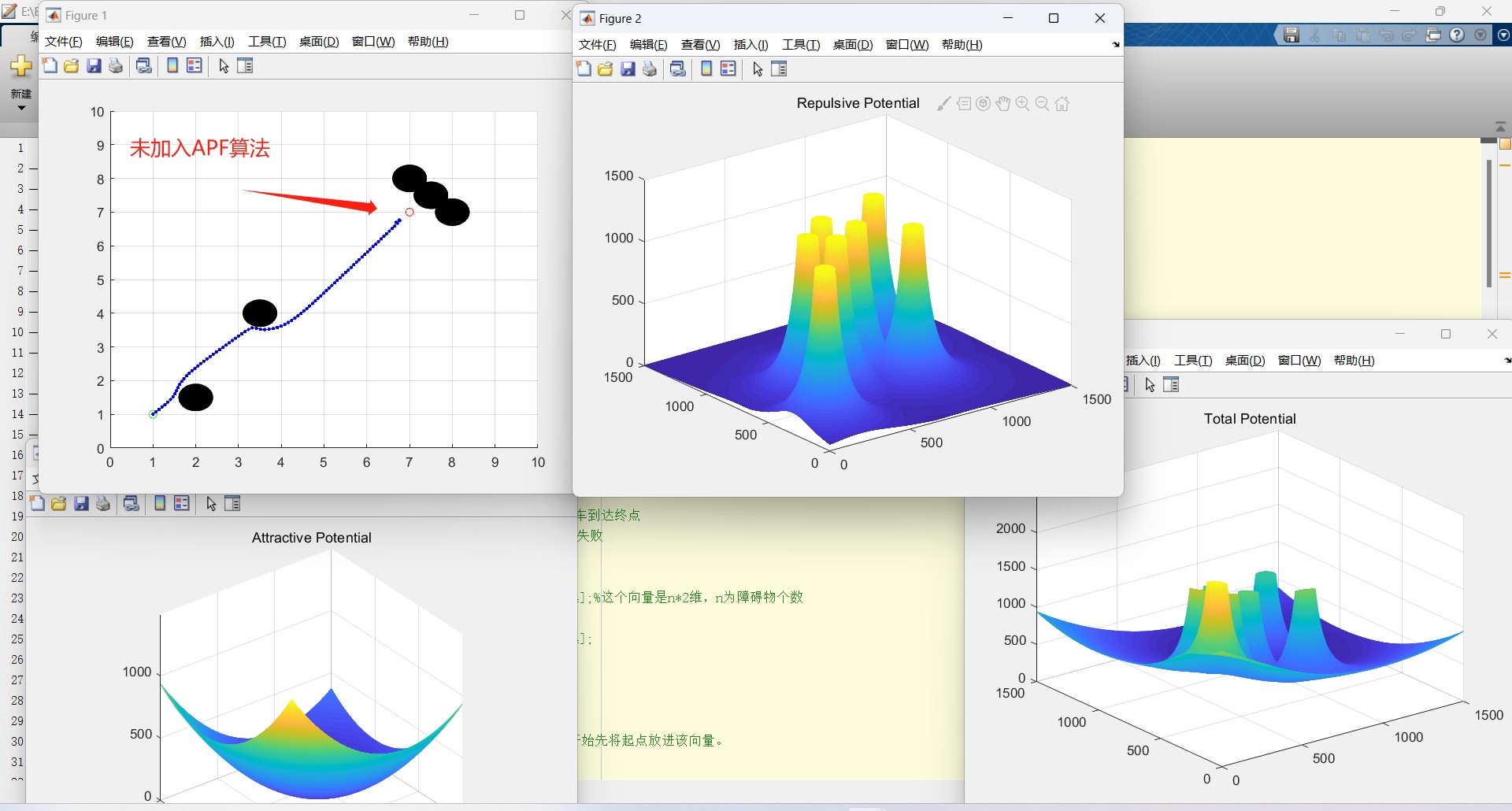
end这段代码里,step_size 是每次移动的步长,机器人从起始点 start 出发,不断计算引力、斥力和合力,按照合力方向移动一小步,记录下路径 path,直到接近目标点。但是呢,就像图里展示的,这种未改进算法很容易陷入局部极小值,导致路径规划失败。
改进的APF算法
改进斥力函数
为了克服局部极小值问题,我们先改进斥力函数。传统斥力函数在某些情况下会导致局部极小,我们可以让斥力函数在远离障碍物时也能起到一定作用,避免机器人过早陷入局部陷阱。
% 改进后的斥力计算
function F_rep_improved = compute_improved_repulsive_force(robot, obstacles, rho0, k)
F_rep_improved = [0, 0];
for i = 1:size(obstacles, 1)
dist = norm(robot - obstacles(i, :));
F_rep_improved = F_rep_improved + k * (1/dist^2) * (robot - obstacles(i, :));
end
end对比之前的斥力函数,这里不再设置距离阈值 rho0,而是让斥力在任何距离都起作用,只是随着距离增大斥力减小的速度更快,这样能引导机器人更好地避开障碍物,减少陷入局部极小的可能。
引入模拟退火算法
除了改进斥力函数,我们还引入模拟退火算法。模拟退火算法可以让机器人有一定概率跳出局部极小值。
% 模拟退火算法参数
T0 = 100; % 初始温度
alpha = 0.95; % 降温系数
T = T0;
while T > 1e-3
F_att = compute_attractive_force(robot, goal, eta);
F_rep = compute_improved_repulsive_force(robot, obstacles, rho0, k);
F_total = F_att + F_rep;
new_robot = robot + step_size * F_total / norm(F_total);
if norm(new_robot - goal) < norm(robot - goal) || exp((norm(robot - goal) - norm(new_robot - goal)) / T) > rand()
robot = new_robot;
end
path = [path; robot];
T = alpha * T;
end在这段代码里,T0 是初始温度,alpha 是降温系数。在每次迭代中,计算新的位置 new_robot,如果新位置更好(离目标更近),或者根据一定概率(与温度 T 有关),就接受新位置。随着温度不断降低,接受较差位置的概率越来越小,最后收敛到较好的路径。

通过这样改进斥力函数和引入模拟退火算法,我们就能有效克服传统APF算法局部极小值和目标不可达的问题,在Matlab模拟的地图中实现更优的路径规划啦。大家不妨自己动手试试,感受下改进前后的差别。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)