——机器人动力学系统具有典型非线性特点，利用TS模糊技术可以实现线性化建模

T-S模糊技术（Takagi-Sugeno模糊模型）是一种基于模糊逻辑的系统建模方法，由日本学者Takagi和Sugeno于1985年提出。该技术通过将非线性系统分解为多个局部线性子系统，并利用模糊规则进行整合，实现对复杂系统的精确建模与控制。

一、典型机器人动力学系统

通常用二阶系统表示低速下的机器人动力学行为：

其中，为惯性矩阵，为粘滞摩擦系数，为负载质量，为重力加速度，为重力加速度至关节转轴的距离，为关节转角，相应其一阶导和二阶导为相应速度和加速度。为控制器信号，直接作用于关节处（红色）。其受力如图所示：

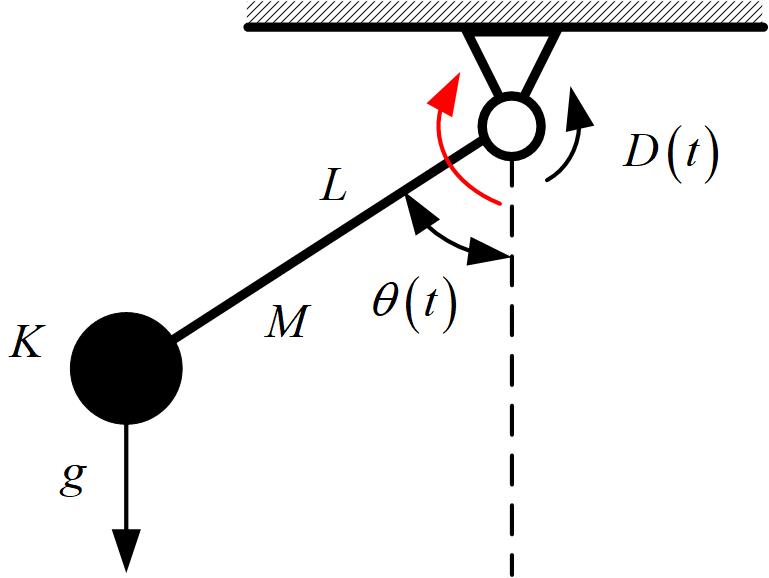
该方程中含有非线性项，无法直接转化为状态空间方程。

例如，可以将上述方程重写为：

令，写成状态空间方程标准形式，可以得到：

注意到，为粘滞摩擦系数，其为时变量。一般状态空间方程中的系数矩阵为了后续控制器能够求解，往往希望其为时不变的常数矩阵。通常，工程上如果短时间使用或是使用得当，粘滞摩擦系数往往用常数的名义摩擦系数代替。

另一个更麻烦且格格不入的项是，它由于含有非线性项而无法加入状态空间方程的线性形式中。该项是由于连杆连接两个不同坐标系所带来的，而机器人中不同坐标系（关节）连接又不可避免也极为复杂。这种情况就是我们经常听到“机器人系统具有强非线性”中非线性的由来，这也是我们需要利用T-S模糊技术线性化的首要目标。该例是单关节机器人的动力学，也是最简单的非线性构成，我们从这种简单情况出发讲解机器人是如何用TS模糊技术线性化的。

二、T—S模糊技术线性化

注意到，非线性项是一个三角函数，且由关节转角决定。对于，对其线性化本质就是希望将其转化为某种的形式（其中C为常数）。

首先能想到的，对于转化为的线性形式，可表达为

其系数函数图像如图所示。

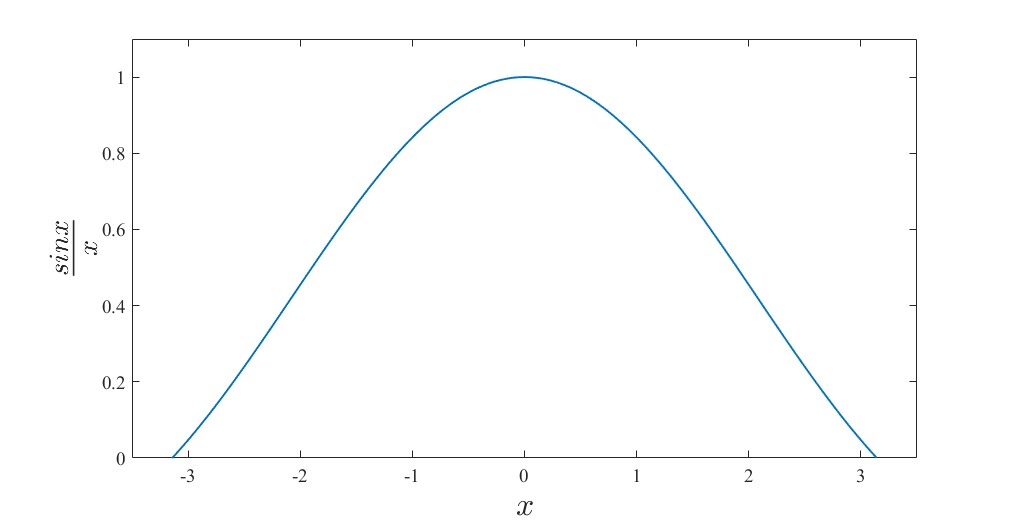
可以看到，只有在x=0附近时，sin(x)与x相近，其比值接近1；越接近，其比值越接近0差异越大。一般在时（约28.6°）时，近似是合理的。同时需要注意到，泰勒展开也是针对x=0附近进行线性化展开的。

因此，可以判定，与无法简单近似。

这里介绍利用TS模糊进行线性化的方法。

观察一下不难发现，属于周期函数，在-1至1之间往复波折。其中，在0处与相等，均为0；当其等于时，。因此我们可以用三角波浪线进行近似。

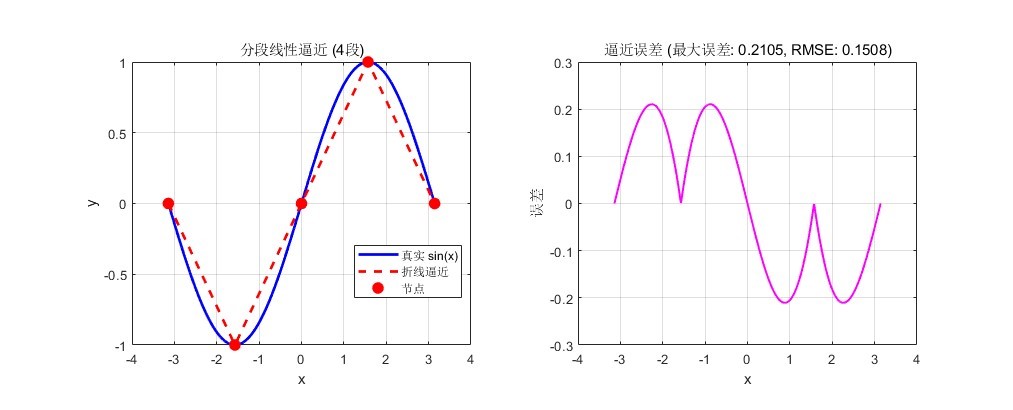
该三角波浪线可以用数学公式进行表示：

可以看到，这属于一种“此消彼长”的运动模式。初步可以分为5个工作点，分别是：

工作点1	工作点2	工作点3	工作点4	工作点5

我们希望其在工作点处可以线性化，满足的形式。因此，我们需要对其求得斜率和偏置。

通过对sin函数在工作点处泰勒展开，可以得到：

,

。

将5个工作点处的值分别带入上述式子，可以得到不同工作点处的线性近似公式：

（1）当时，

。

（2）当时，

。

（3）当时，

。

（4）当时，

。

（5）当时，

。

除了工作点处，其余sin函数处的曲线可以看成是该5条直线的“加成”，如下图所示。

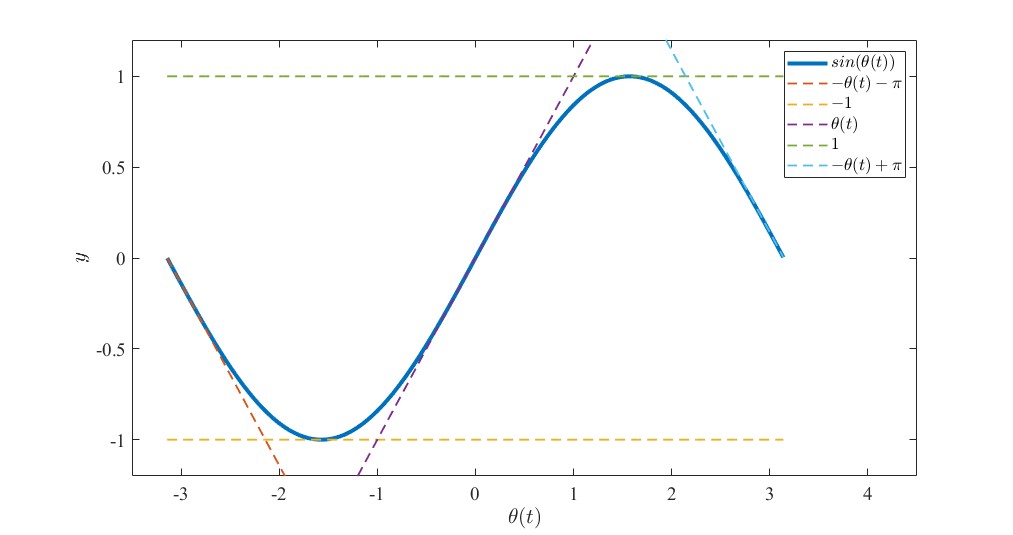
可以看到，sin(x)函数可以由这5条直线近似化而成，可以看一下它与原曲线的误差变化。

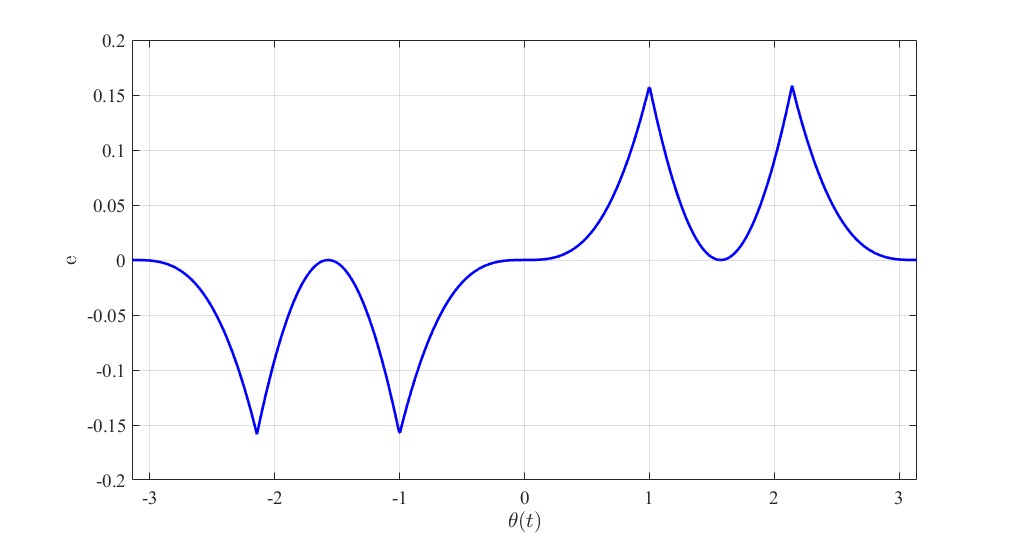
相较于前述的3段折线最大误差略有减小，这主要是泰勒展开的功劳。误差虽不大，但是仍旧存在。因此对于这些工作点间的误差大的曲线，需要用模糊技术圆滑过渡修饰一下。如何过渡呢？就是拿一点前面的拿一点后面的，和稀泥一下得到一点承上启下的。至于拿多少，则需要用隶属度函数来确定。隶属度，就是有多少成分属于前面还是后面的工作点。

三角形函数是最简单的，有一个明显起降过程，也就是我们需要的过渡过程。在工作点隶属度可以拉满设置为1，在其它非工作点逐渐淡化至0.

针对这个“5点4段线”可以设置5个三角隶属函数。其中，隶属函数具体设计如下：

我们可以绘制出这5条隶属函数的图像。

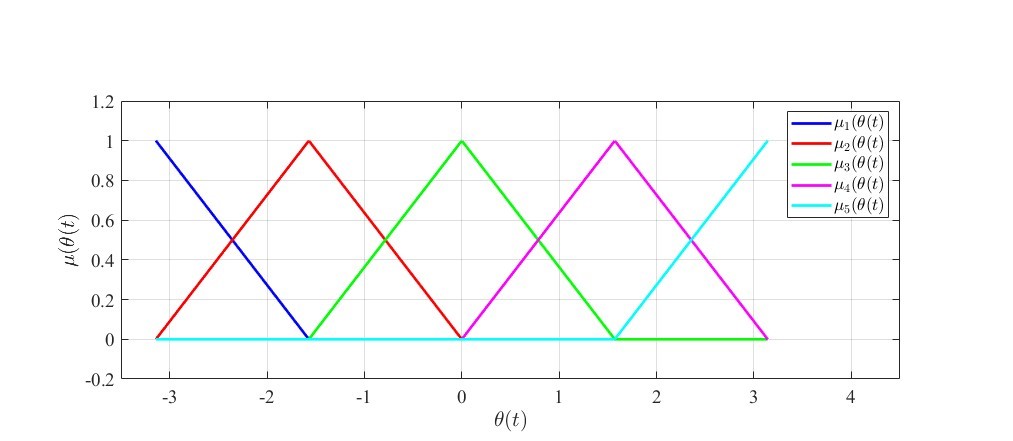
可以看到，这些隶属函数一直保证在中取任意数值时，。而且在任意工作点处，都是此消彼长的关系，符合的我们的线性化趋势。

因此，可以使用模糊推理得出，T-S模糊系统中输出为各规则输出的加权和：

需要注意的是，某一取值下，并不要求严格，这只是针对满足单位划分的情况下。例如，当出现高斯隶属函数时，。因此，上式可以进一步简化为：

至此，我们完成了基于T—S模糊技术的线性化过程。

三、T—S模糊技术在机器人动力学中的应用。

我们知道了机器人动力学的非线性方程：

其中非线性特性是由引起的。

我们也知道了如何利用T-S模糊技术处理对其进行线性化近似：

因此，我们可以基于T-S模糊技术将机器人动力学线性化。

规则1：如果在附近（），则：

规则2：如果在附近（），则：

规则3：如果在附近（），则：

规则4：如果在附近（），则：

规则5：如果在附近（），则：

当在上的其它区域时，则可表示为这5个动力学系统关于隶属函数的加权和。

可以利用MATLAB中的SIMULINK验证改模糊方法的准确性。

假设初始状态为，此时机械臂相当于是平举。假如不施加控制力矩，机械臂按理说应该受重力作用下摆运动，然后收摩擦阻力影响摆幅逐渐减小，直至停留在的位置处，实际也是如此，如图所示。

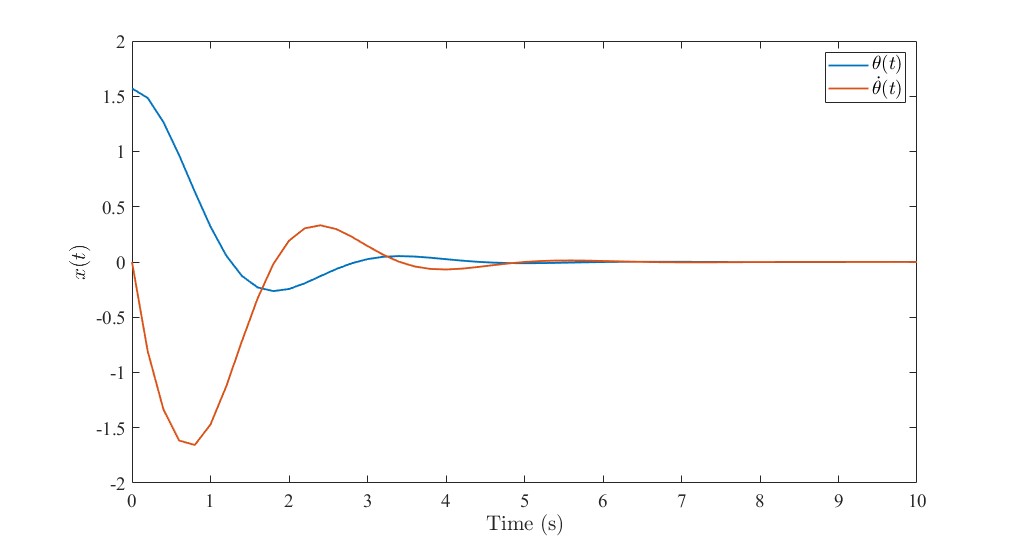
该机械臂设置，，，，，单位均为国际标准单位。

同样，可以根据前述5点4段模糊模型，仿真出T-S模糊系统输出曲线，如下图所示。

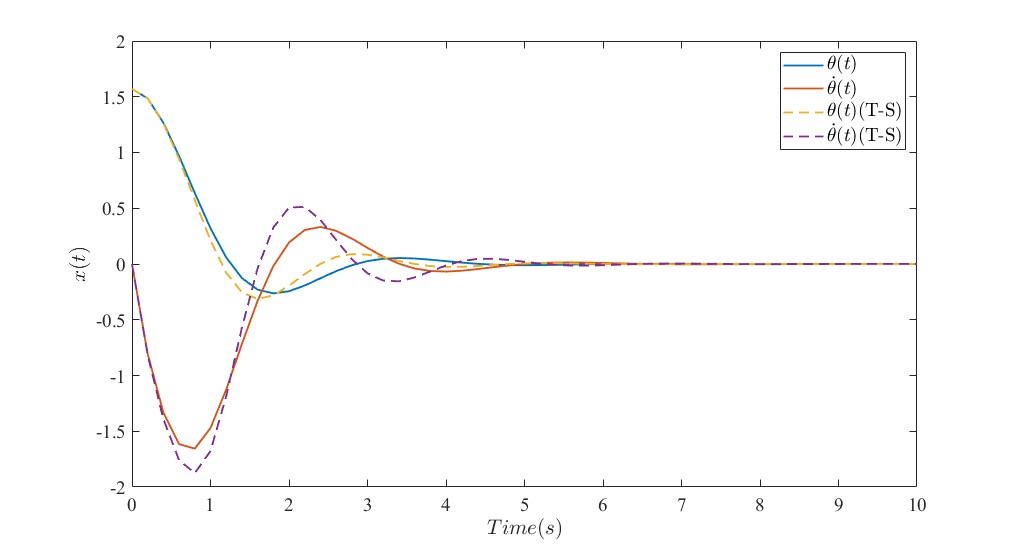
此时我们很容易发现，虚线为模糊系统的响应输出曲线，与实际系统输出曲线存在较大差异，并未完成近似的功能。

究其原因是由于带了后面的常数项，此时系统并未变成线性系统，而是成为了仿射系统。

通常，线性系统的表现形式为，而仿射系统作为介于线性与非线性系统的中间态，其表现形式为，其中往往代表了非线性项，其不满足线性叠加原理，因此无法简单用T-S模糊方法分解。

那该如何办呢？其实稍微改进一下原机器人动力学方程就可以了。

注意到，主要是利用了的方式与产生联系进而将非线性项线性化，然而其中在不同情况下容易引入进而导致系统无法成为线性系统。可以换个思路，直接将变为这种比例乘法形式，避免了常数项的产生，进而避免了系统演变为仿射系统。不要怕系数项变复杂，同样我们可以利用T-S模糊的方法处理。

基于上述结论，我们可以得到机器人动力学方程表达式为：

令，此时，。系统矩阵A(t)是时变的，其中可以用名义粘滞系数简化表示，但是要如何变为常数项呢？这里需要借助

T-S模糊的方法。

首先来观察一下在区间上的图像，见前第二张图，可以看到它是一个光滑的偶函数。当时，；当远离0时，逐渐减小缩小至0。我们不希望矩阵A出现第一列空白的，所以我们取一个无限小值替代0。

与前述T-S模糊方法一样的线性化手段，选取进行线性化展开。对于而言，没有区别，因此，我们可以得到T-S模糊的动力学模型规则：

规则1：如果接近于0，则系统模型表示为：

其中，。

规则2：如果接近于，则系统模型表示为：

其中，。

接下来需要定义两个模糊隶属函数和，其需满足。用最简单的比例加权函数作为隶属函数就可以，例如

可以看到，这两个模糊隶属函数和相当于表示了分别与1和的距离。

接下来就剩这个，它应该是一个很小的数，在文献中通常取。

因此，经T-S模糊化后的线性机器人动力学系统可以变为：

同样经过SIMULINK仿真可以得到

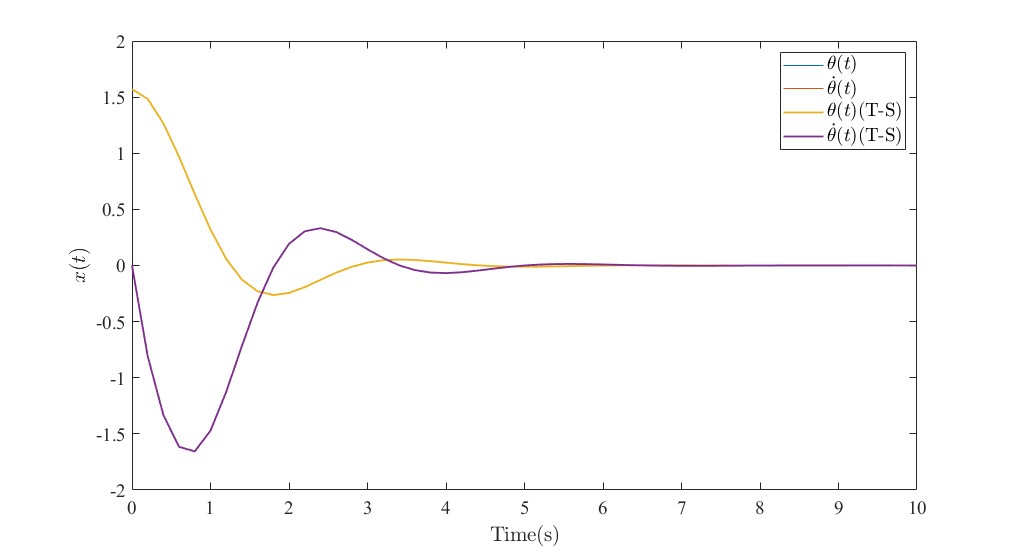
其误差曲线如图所示。

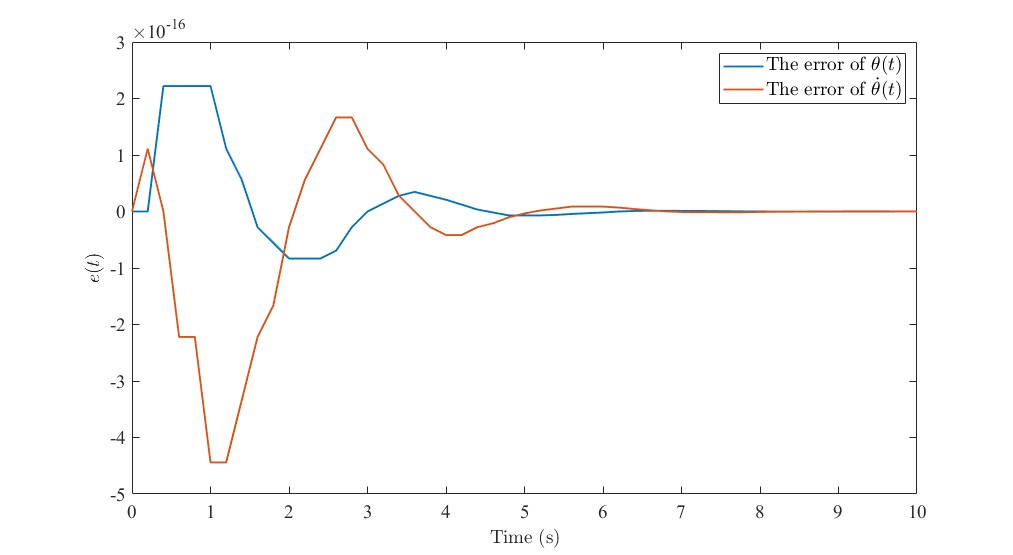
我们可以看到，当T-S模糊后的系统从仿射系统变成线性系统后，其误差相较于原始非线性系统而言非常小，几乎是0。由此可见T-S模糊方法在机器人系统这一典型非线性系统中线性化的优势。