机器学习之逻辑回归
逻辑回归(Logistic回归)又称Logistic回归分析,是机器学习中的一种分类模型,虽然名字中带有回归,但其是用来解决分类问题的。常用于数据挖掘,疾病自动诊断,经济预测等领域。逻辑回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在 0 和 1 之间。logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。
一、逻辑回归的概念
1.1 简介
逻辑回归(Logistic回归)又称Logistic回归分析,是机器学习中的一种分类模型,虽然名字中带有回归,但其是用来解决分类问题的。常用于数据挖掘,疾病自动诊断,经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在 0 和 1 之间。logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。
1.2 算法原理
线性分类器,是一种假设特征与分类结果存在线性关系的模型。这个模型通过累加计算每个维度的特征与各自权重的乘积来帮助类别决策。
假设我们输入数据的特征定义为 来代表n维特征列向量,用
来代表对应的权重,或者叫做系数,同时为了避免其过坐标原点这种硬性假设,增加一个截距 b。由此这种线性关系可以表示为:
我们要处理最简单的二分类问题,就需要把一个函数值映射到(0,1)之间,所以我们就希望有一个函数能帮我们完成这个转化,于是便找到了逻辑函数 Sigmoid(max重要) 来替代。
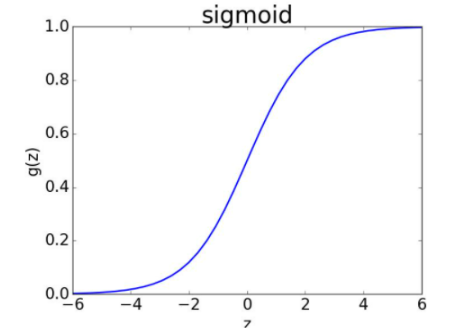
1.3 优缺点
优点:
- 计算效率高:逻辑回归的计算成本相对较低,因为它只涉及线性计算和sigmoid函数。
- 易于理解和实现:逻辑回归的模型简单,易于理解和解释。
- 不需要数据归一化:与一些其他算法不同,逻辑回归不需要对特征进行严格的归一化处理。
缺点:
- 对非线性数据效果不佳:当数据不是线性可分时,逻辑回归的效果可能不佳。
- 对特征工程敏感:逻辑回归的性能很大程度上取决于特征的选择和构造。
- 容易过拟合:当模型复杂度过高或样本量较少时,逻辑回归容易过拟合。
二、模型训练
在逻辑回归中,我们通常使用最大似然估计(Maximum Likelihood Estimation)来估计参数 ( \theta )。具体地,我们试图找到一组参数,使得在这组参数下,样本的观测值出现的概率最大。这通常通过最小化损失函数(如交叉熵损失)来实现。
三、线性回归和逻辑回归的基本区别
因变量处理方式不同:线性回归中,因变量y处于被解释的特殊地位,由自变量x解释;而逻辑回归中,因变量表示某种事件发生与否的概率,不直接由自变量解释。
对应数据类型不同:线性回归自变量和因变量都可以是随机变量,而逻辑回归的因变量是概率,通常取值范围在0和1之间,表示事件发生概率。
研究目的和对象不同:线性回归适用于预测因变量的数值结果,可以量化影响大小;而逻辑回归更适用于解决分类问题,如二分类问题中的“是”或“否”。
四、逻辑回归模型构造
4.1 需求
逻辑回归模型可以看成是线性回归+sigmoid函数
线性回归:z=w*x+b
sigmoid函数: y=1/(1+e^(-z))
逻辑回归:y=1/(1+e^(-w*x+b))
所以求解一个好的逻辑回归只需要求解最佳的w和b即可
4.2 代价函数
1)代价函数是体现“预测值”与“实际值”相似程度的函数
2)代价函数越小,模型越好
线性回归的代价函数:
若逻辑回归也是采用此代价函数,可如下图所示:
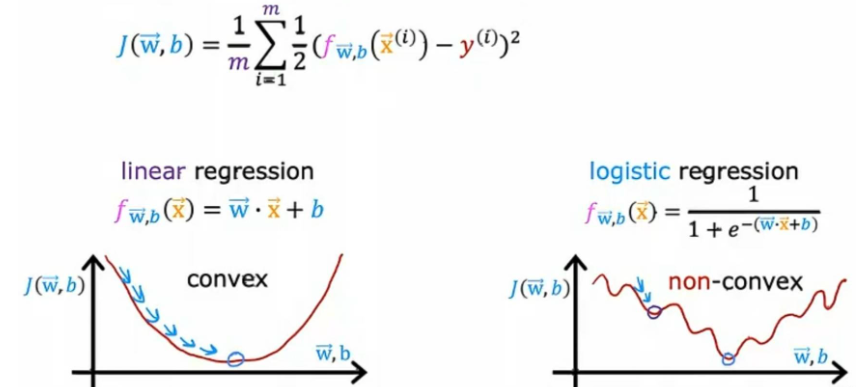
逻辑回归的代价函数将会是非凸代价函数不凸,意味着如果尝试使用梯度下降可能会陷入很多局部最小值。所以平方误差代价函数对逻辑回归来说不是一个好的选择。
五、实战演练
5.1 代码示例
5.1.1 数据集
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
0.667394 12.741452 0
-2.460150 6.866805 1
0.569411 9.548755 0
-0.026632 10.427743 0
0.850433 6.920334 1
1.347183 13.175500 0
1.176813 3.167020 1
-1.781871 9.097953 0
-0.566606 5.749003 1
0.931635 1.589505 1
-0.024205 6.151823 1
-0.036453 2.690988 1
-0.196949 0.444165 1
1.014459 5.754399 1
1.985298 3.230619 1
-1.693453 -0.557540 1
-0.576525 11.778922 0
-0.346811 -1.678730 1
-2.124484 2.672471 1
1.217916 9.597015 0
-0.733928 9.098687 0
-3.642001 -1.618087 1
0.315985 3.523953 1
1.416614 9.619232 0
-0.386323 3.989286 1
0.556921 8.294984 1
1.224863 11.587360 0
-1.347803 -2.406051 1
1.196604 4.951851 1
0.275221 9.543647 0
0.470575 9.332488 0
-1.889567 9.542662 0
-1.527893 12.150579 0
-1.185247 11.309318 0
-0.445678 3.297303 1
1.042222 6.105155 1
-0.618787 10.320986 0
1.152083 0.548467 1
0.828534 2.676045 1
-1.237728 10.549033 0
-0.683565 -2.166125 1
0.229456 5.921938 1
-0.959885 11.555336 0
0.492911 10.993324 0
0.184992 8.721488 0
-0.355715 10.325976 0
-0.397822 8.058397 0
0.824839 13.730343 0
1.507278 5.027866 1
0.099671 6.835839 1
-0.344008 10.717485 0
1.785928 7.718645 1
-0.918801 11.560217 0
-0.364009 4.747300 1
-0.841722 4.119083 1
0.490426 1.960539 1
-0.007194 9.075792 0
0.356107 12.447863 0
0.342578 12.281162 0
-0.810823 -1.466018 1
2.530777 6.476801 1
1.296683 11.607559 0
0.475487 12.040035 0
-0.783277 11.009725 0
0.074798 11.023650 0
-1.337472 0.468339 1
-0.102781 13.763651 0
-0.147324 2.874846 1
0.518389 9.887035 0
1.015399 7.571882 0
-1.658086 -0.027255 1
1.319944 2.171228 1
2.056216 5.019981 1
-0.851633 4.375691 1
-1.510047 6.061992 0
-1.076637 -3.181888 1
1.821096 10.283990 0
3.010150 8.401766 1
-1.099458 1.688274 1
-0.834872 -1.733869 1
-0.846637 3.849075 1
1.400102 12.628781 0
1.752842 5.468166 1
0.078557 0.059736 1
0.089392 -0.715300 1
1.825662 12.693808 0
0.197445 9.744638 0
0.126117 0.922311 1
-0.679797 1.220530 1
0.677983 2.556666 1
0.761349 10.693862 0
-2.168791 0.143632 1
1.388610 9.341997 0
0.317029 14.739025 05.1.2 代码实战
import sys
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# Logistic 回归梯度上升优化算法
def load_data_set():
# 创建两个列表
data_mat = []
label_mat = []
try:
# 打开文件
fr = open("C:\\Users\\86136\\Desktop\\testSet.txt")
except FileNotFoundError:
print("错误:文件 'testSet.txt' 未找到。请确保文件存在并位于正确的路径下。")
return data_mat, label_mat
for line in fr.readlines():
# 对当前行去除首尾空格,并按空格进行分离
line_arr = line.strip().split()
data_mat.append([1.0, float(line_arr[0]), float(line_arr[1])])
label_mat.append(int(line_arr[2]))
fr.close()
return data_mat, label_mat
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
def grad_ascent(data_mat_in, class_labels):
# 将输入的数据转换为NumPy矩阵
data_matrix = np.asmatrix(data_mat_in)
# 将类别标签转换为NumPy矩阵,并进行转置,使其成为列向量
label_mat = np.asmatrix(class_labels).transpose()
# 获取数据矩阵的行数和列数
m, n = np.shape(data_matrix)
# 设置学习率
alpha = 0.001
# 设置最大迭代次数
max_cycles = 500
# 初始化权重为n行1列的矩阵,元素全部为1
weights = np.ones((n, 1))
# 进行最大迭代次数的循环
for k in range(max_cycles):
# 计算当前权重下的预测值,使用sigmoid函数
h = sigmoid(data_matrix * weights)
# 计算预测值与实际值之间的误差
error = (label_mat - h)
# 更新权重:权重+学习率*数据矩阵的转置*误差
weights = weights + alpha * data_matrix.transpose() * error
# 返回训练好的权重
return weights
# 画出数据集和Logistic回归最佳拟合直线的函数
def plot_best_fit(weights):
# 导入matplotlib.pyplot模块用于绘图
import matplotlib.pyplot as plt
# 加载数据集
data_mat, label_mat = load_data_set()
# 将数据矩阵转换为NumPy数组
data_arr = np.array(data_mat)
# 获取数据点的数量
n = np.shape(data_arr)[0]
# 初始化两个列表,分别用于存储正类和负类的x坐标和y坐标
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
# 遍历所有数据点,将它们分类到正类或负类
for i in range(n):
if int(label_mat[i]) == 1:
# 如果标签为1,则将数据点的x和y坐标分别添加到正类的列表中
xcord1.append(data_arr[i, 1])
ycord1.append(data_arr[i, 2])
else:
# 如果标签不为1,则将数据点的x和y坐标分别添加到负类的列表中
xcord2.append(data_arr[i, 1])
ycord2.append(data_arr[i, 2])
# 创建一个新图形
fig = plt.figure()
# 在图形中添加一个子图
ax = fig.add_subplot(111)
# 在子图中绘制正类数据点的散点图,使用红色方块标记
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
# 在子图中绘制负类数据点的散点图,使用绿色标记
ax.scatter(xcord2, ycord2, s=30, c='green')
# 创建一个x值的范围,用于绘制最佳拟合直线
x = np.arange(-3.0, 3.0, 0.1)
# 根据权重计算对应的y值
y = (-weights[0] - weights[1] * x) / weights[2]
# 在子图中绘制最佳拟合直线
ax.plot(x, y)
# 设置x轴标签
plt.xlabel('X1')
# 设置y轴标签
plt.ylabel('X2')
# 显示图形
plt.show()
# 主程序
dataMat, labelMat = load_data_set()
if dataMat and labelMat:
weights = grad_ascent(dataMat, labelMat)
plot_best_fit(weights.getA())5.2 结果展示
得到的图像就像这样:
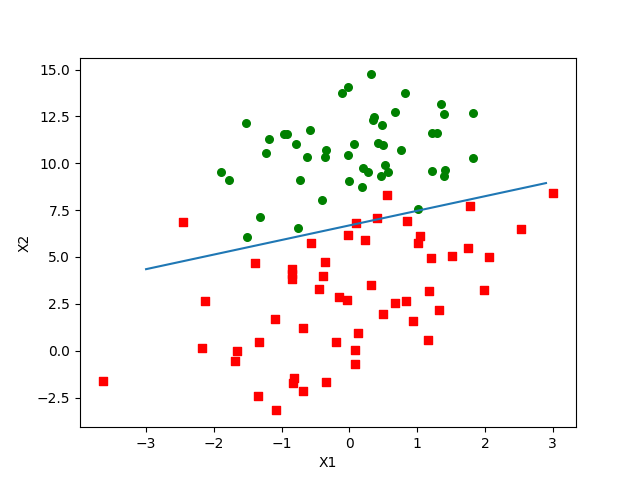

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容






所有评论(0)