二连杆机器人动力学——机械臂动力学计算实例

1. 机器人系统模型假设一个二连杆机械臂结构如图所示。其中，机械臂的质量主要富集于机器人关节处，分别为：、；机械臂连杆长度分别为：、；机械臂关节运动为纯旋转，所以仅存在为角度的广义坐标：、；重力加速度为：。根据定义拉格朗日方程：其中，L为拉格朗日函数，而K为系统广义动能，P为系统广义位能；为连杆子系统索引号（）；为第个子系统的动能和位能的坐标（位移和角度），为相应的广义速度（线速度和角速度）；为第

hello我是小菜鸡

24637人浏览 · 2021-04-05 22:50:07

hello我是小菜鸡 · 2021-04-05 22:50:07 发布

1. 机器人系统模型

假设一个二连杆机械臂结构如图所示。

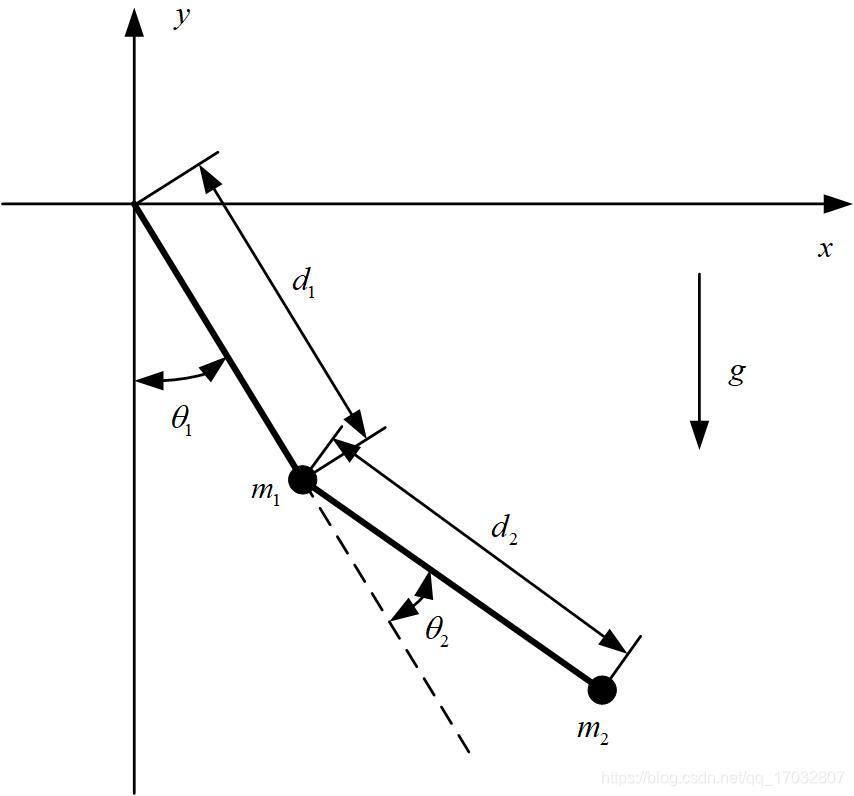
其中，

机械臂的质量主要富集于机器人关节处，分别为： $m_1$ 、 $m_2$ ；机械臂连杆长度分别为： $d_1$ 、 $d_2$ ；机械臂关节运动为纯旋转，所以仅存在为角度的广义坐标： $\theta _1$ 、 $\theta _2$ ；重力加速度为： $g$ 。

根据定义

拉格朗日方程：

$F_{i}=\frac{d}{dt} \frac{\partial L }{\partial \dot{q}_{i}} - \frac{\partial L }{\partial \dot{q}_{i}},i=1,2,...,n$

其中，

L为拉格朗日函数 $L=K-P$ ，而K为系统广义动能，P为系统广义位能；

$i$ 为连杆子系统索引号（ $i=1,2,...$ ）； $q_i$ 为第 $i$ 个子系统的动能和位能的坐标（位移和角度）， $\dot{q}_i$ 为相应的广义速度（线速度和角速度）； $F_{i}$ 为第 $i$ 个子系统的广义力（力和力矩）。

2. 计算各个连杆的动能及位能

该二连杆机器人系统可将机器人拆解为两个单独连杆（连杆1和连杆2 ）的子系统。

2.1 连杆1的动能

$K_1 \\= \frac{1}{2} m_1 v_{1}^{2} \\=\frac{1}{2} m_1 \left ( \left (\frac{d}{dt}(d_1 sin \theta_1) \right )^2 + \left (\frac{d}{dt}(-d_1 cos \theta_1) \right )^2 \right ) \\ = \frac{1}{2} m_1 \left ( \left ( d_1 cos \theta_1 \dot{\theta}_1 \right )^2 + \left ( d_1 sin \theta_1 \dot{\theta}_1\right )^2 \right ) \\=\frac{1}{2} m_1 d_1^{2} \left ( cos^2 \theta_1+sin^2 \theta_1 \right ) \dot{\theta}_{1}^{2} \\ = \frac{1}{2} m_1 d_1^{2} \dot{\theta}_{1}^{2}$

2.2 连杆1的位能

$P_{1}\\=m_{1}g h_{1} \\= m_{1}g(-d_{1} cos \theta _{1}) \\= - m_{1} g d_{1} cos \theta_{1}$

2.3 连杆2的动能

$K_2 \\= \frac{1}{2} m_2 v_{2}^{2}\\=\frac{1}{2} m_2 \left ( (\frac{d }{d t} (d_1 sin \theta _1 + d_2 sin(\theta _1 + \theta _2)))^{2}+ (\frac{d }{d t} (-d_1 cos \theta _1 - d_2 cos(\theta _1 + \theta _2)))^{2}\right ) \\=\frac{1}{2} m_2 \left ( \left ( d_1 cos \theta_1 \dot{\theta}_1 + d_2 cos (\theta_1 + \theta_2)(\dot{\theta}_1 + \dot{\theta}_2) \right )^{2} +\left(d_1 sin \theta_1 \dot{\theta}_1 + d_2 sin(\theta_1 + \theta_2)(\dot{\theta_1}+\dot{\theta_2})\right)^2 \right ) \\=\frac{1}{2} m_2\left ( d_1^2 \dot{\theta}_{1}^{2} + d_{2}^{2}\left ( \dot{\theta}_1^{2}+2\dot{\theta}_1 \dot{\theta}_2 + \dot{\theta}_2^2 \right ) +2d_1 d_2 cos \theta_2 (\dot{\theta}_1^2 + \dot{\theta}_1 \dot{\theta}_2)\right ) \\=\frac{1}{2} m_2 d_1^2 \dot{\theta}_{1}^{2} + \frac{1}{2} m_2 d_{2}^{2}\left ( \dot{\theta}_1^{2}+2\dot{\theta}_1 \dot{\theta}_2 + \dot{\theta}_2^2 \right ) +m_2 d_1 d_2 cos \theta_2 (\dot{\theta}_1^2 + \dot{\theta}_1 \dot{\theta}_2)$

2.4 连杆2的位能

$P_{2}\\=m_{2}g h_{2} \\= m_{2}g(-d_{1} cos \theta _{1} - d_2 cos(\theta_1 + \theta_2)) \\= - m_{2} g d_{1} cos \theta_{1} - m_{2} g d_{1} cos(\theta_1 + \theta_2)$

2.5 系统总能量

总动能：

$K \\= K_1 + K_2 \\=\frac{1}{2} m_1 d_1^{2} \dot{\theta}_{1}^{2}+\frac{1}{2} m_2 d_1^2 \dot{\theta}_{1}^{2} + \frac{1}{2} m_2 d_{2}^{2}\left ( \dot{\theta}_1^{2}+2\dot{\theta}_1 \dot{\theta}_2 + \dot{\theta}_2^2 \right ) +m_2 d_1 d_2 cos \theta_2 (\dot{\theta}_1^2 + \dot{\theta}_1 \dot{\theta}_2) \\=\frac{1}{2} \left (m_1 +m_2 \right ) d_1^{2} \dot{\theta}_{1}^{2} + \frac{1}{2} m_2 d_{2}^{2}\left ( \dot{\theta}_1^{2}+2\dot{\theta}_1 \dot{\theta}_2 + \dot{\theta}_2^2 \right ) +m_2 d_1 d_2 cos \theta_2 (\dot{\theta}_1^2 + \dot{\theta}_1 \dot{\theta}_2)$

总位能

$P\\=P_1 + P_2 \\=- m_{1} g d_{1} cos \theta_{1}- m_{2} g d_{1} cos \theta_{1} - m_{2} g d_{1} cos(\theta_1 + \theta_2) \\ = - \left (m_{1} +m_2 \right ) g d_{1} cos \theta_{1}- m_{2} g d_{1} cos(\theta_1 + \theta_2)$

3. 拉格朗日平衡法求动力学方程

二连杆机械臂的拉格朗日函数L可以计算得：

$L \\=K-P \\=\frac{1}{2} \left (m_1 +m_2 \right ) d_1^{2} \dot{\theta}_{1}^{2} + \frac{1}{2} m_2 d_{2}^{2}\left ( \dot{\theta}_1^{2}+2\dot{\theta}_1 \dot{\theta}_2 + \dot{\theta}_2^2 \right ) +m_2 d_1 d_2 cos \theta_2 (\dot{\theta}_1^2 + \dot{\theta}_1 \dot{\theta}_2)\\+ \left (m_{1} +m_2 \right ) g d_{1} cos \theta_{1}+ m_{2} g d_{1} cos(\theta_1 + \theta_2)$

让L对分别对 $\theta _1, \theta_2, \dot{\theta}_1, \dot{\theta}_2$ 进行求导：

$\frac{\partial L}{\partial \theta_1} \\ = -(m_1 + m_2) g d_1 sin \theta_1 - m_2 g d_1 sin(\theta_1 + \theta_2)$ ；

$\frac{\partial L }{\partial \theta_2} \\= -m_2 d_1 d_2 sin \theta_2 (\dot{\theta}_1^2 + \dot{\theta}_1 \dot{\theta}_2)- m_2 g d_1 sin(\theta_1+\theta_2)$ ；

$\frac{\partial L}{\partial \dot{\theta}_1} \\= (m_1 + m_2) d_1^2 \dot{\theta}_1 + m_2 d_2^2 \dot{\theta}_1 + m_2 d_2^2 \dot{\theta}_2 + 2 m_2 d_1 d_2 cos \theta_2 \dot{\theta}_1 + m_2 d_1 d_2 cos \theta_2 \dot{\theta}_2$

$\frac{\partial L}{\partial \dot{\theta}_2} \\=m_2 d_2 ^2 \dot{\theta}_1+m_2 d_2 ^2 \dot{\theta}_2 + m_2 d_1 d_2 cos \theta_2 \dot{\theta}_1$

$\frac{d}{dt} \frac{\partial L }{\partial \dot{\theta}_1} \\= (m_1 + m_2) d_1^2 \ddot{\theta}_1 + m_2 d_2^2 \ddot{\theta}_1 + m_2 d_2^2 \ddot{\theta}_2 - 2m_2 d_1 d_2 sin \theta _2 \dot{\theta}_1 \dot{\theta}_2 + 2m_2 d_1 d_2 cos \theta_2 \ddot{\theta}_1 - m_2 d_1 d_2 sin \theta_2 \dot{\theta}_2^2 + m_2 d_1 d_2 cos \theta_2 \ddot{\theta}_2 \\= \left [ (m_1 + m_2) d_1^2 + m_2 d_2^2 + 2m_2 d_1 d_2 cos \theta_2 \right ] \ddot{\theta}_1 + \left ( m_2 d_2^2 + m_2 d_1 d_2 cos \theta_2 \right ) \ddot{\theta}_2 \\- 2 m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1 \dot{\theta}_2 - m_2 d_1 d_2 sin \theta_2 \dot{\theta}_2^2$

$\frac{d}{dt} \frac{\partial L }{\partial \dot{\theta}_2} \\= m_2 d_2^2 \ddot{\theta}_1 + m_2 d_2^2 \ddot{\theta}_2 + m_2 d_1 d_2 cos \theta_2 \ddot{\theta}_1 - m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1 \dot{\theta}_2$

机械臂各关节力矩分别为 $T_1,T_2$ ，根据拉格朗日方程可以得到：

$T_1 \\ = \frac{d}{dt} \frac{\partial L }{\partial \dot{\theta}_1}-\frac{\partial L}{\partial \theta_1} \\=\left [ (m_1 + m_2) d_1^2 + m_2 d_2^2 + 2m_2 d_1 d_2 cos \theta_2 \right ] \ddot{\theta}_1 + \left ( m_2 d_2^2 + m_2 d_1 d_2 cos \theta_2 \right ) \ddot{\theta}_2 \\- 2 m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1 \dot{\theta}_2 - m_2 d_1 d_2 sin \theta_2 \dot{\theta}_2^2 +(m_1 + m_2) g d_1 sin \theta_1 + m_2 g d_1 sin(\theta_1 + \theta_2)$

$T_2 \\ = \frac{d}{dt} \frac{\partial L }{\partial \dot{\theta}_2}-\frac{\partial L}{\partial \theta_2} \\= m_2 d_2^2 \ddot{\theta}_1 + m_2 d_2^2 \ddot{\theta}_2 + m_2 d_1 d_2 cos \theta_2 \ddot{\theta}_1+m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1^2 + m_2 g d_1 sin(\theta_1+\theta_2)$

整理成动力学方程，

$\left\{\begin{matrix} T_1 = \left [ (m_1 + m_2) d_1^2 + m_2 d_2^2 + 2m_2 d_1 d_2 cos \theta_2 \right ] \ddot{\theta}_1 + \left ( m_2 d_2^2 + m_2 d_1 d_2 cos \theta_2 \right ) \ddot{\theta}_2 \\- 2 m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1 \dot{\theta}_2 - m_2 d_1 d_2 sin \theta_2 \dot{\theta}_2^2 +(m_1 + m_2) g d_1 sin \theta_1 + m_2 g d_1 sin(\theta_1 + \theta_2) \\ T_2 = \left (m_2 d_2^2 + m_2 d_1 d_2 cos \theta_2 \right )\ddot{\theta}_1 + m_2 d_2^2 \ddot{\theta}_2 +m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1^2 + m_2 g d_1 sin(\theta_1+\theta_2)\end{matrix}\right.$

写成矩阵形式

$\begin{bmatrix} T_1\\ T_2 \end{bmatrix} \\=\begin{bmatrix} (m_1 + m_2) d_1^2 + m_2 d_2^2 + 2m_2 d_1 d_2 cos \theta_2 & m_2 d_2^2 + m_2 d_1 d_2 cos \theta_2\\ m_2 d_2^2 + m_2 d_1 d_2 cos \theta_2 & m_2 d_2^2 \end{bmatrix} \begin{bmatrix} \ddot{\theta}_1\\ \ddot{\theta}_2 \end{bmatrix} \\+ \begin{bmatrix} 0 & -2m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1-m_2 d_1 d_2 sin \theta_2 \dot{\theta}_2\\ m_2 d_1 d_2 sin \theta_2 \dot{\theta}_1 & 0 \end{bmatrix} \begin{bmatrix} \dot{\theta}_1\\ \dot{\theta}_2 \end{bmatrix} \\+\begin{bmatrix} (m_1 + m_2)gd_1 sin \theta_1 + m_2 g d_1 sin(\theta_1 +\theta_2)\\ m_2 g d_1 sin(\theta_1 + \theta_2) \end{bmatrix}$

通常上述矩阵形式可以用二阶非线性微分方程描述：

$\tau =M(q) \ddot{q}+C(q,\dot{q}) \dot{q}+G(q)$

其中， $q,\dot{q},\ddot{q}$ 分别为机器人广义坐标、广义速度、广义加速度； $M(q)$ 为机械臂惯性矩阵； $C(q,\dot{q})$ 表示离心力和科氏力矩阵； $G(q)$ 表示机器人重力矩阵； $\tau$ 表示机器人广义力。

常用性质：

性质1： $M(q)-2C(q,\dot{q})$ 是一个斜对称矩阵；

性质2： $M(q)$ 是一个对称正定矩阵；

DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

草莓采摘机器人结构设计2张cad＋设计说明书＋三维图

2022年，山东省的智慧农业项目中，草莓采摘机器人被广泛应用于大棚种植，提升了采摘效率和作业质量，根据市场调研，预计到2024年，草莓采摘机器人将会在技术上进一步升级，性能和效率将得到提升，市场需求也将持续增长[8]。(1)提高生产效率：顾名思义，提升生产效率是所有设备的关键因素，也是各个技术的突破点，草莓采摘机器人能够在短时间内完成大量的采摘工作，将会显著提高生产效率，降低人工成本。(3)提升采

DAMO开发者矩阵

【磁场】扩展卡尔曼滤波器用于利用高斯过程回归进行磁场SLAM研究附Matlab代码

同步定位与地图构建（Simultaneous Localization and Mapping, SLAM）是自主移动机器人实现未知环境自主导航的核心技术。传统视觉、激光SLAM在光照变化剧烈、遮挡严重或无纹理环境中易失效，而磁场SLAM凭借地磁场的全域分布、稳定性强、不受光照遮挡影响等独特优势，成为复杂环境下SLAM技术的重要补充方案。高斯过程回归（Gaussian Process Regres