目录

 1. 介绍

1.1 XGboost简单介绍

1.2 数据集基本情况回顾

2. 数据准备

2.1 特征构造

2.2  数据准备

3. XGBOOST模型

3.1 模型搭建

3.2 特征重要性

3.3 模型评估

3.4 对比真实值和预测值

总结

---

 1. 介绍

在“加州房价（California Housing Prices）数据集（一）—— 数据集的预处理”一文中，已介绍了该数据集的基本情况，同时，文章还探讨了如何针对该数据集的描述性分析以及变量间的相关性分析。如需查看请转到下方链接：

​​​​​​https://blog.csdn.net/rainbow_baby/article/details/152127894?spm=1001.2014.3001.5502

https://blog.csdn.net/rainbow_baby/article/details/152127894?spm=1001.2014.3001.5502

接下来，承接上文的数据预处理工作，将重点展开特征工程构建与预测模型搭建的具体实践。

1.1 XGboost简单介绍

XGBoost（全称为 eXtreme Gradient Boosting，极限梯度提升）是一种基于决策树的集成学习算法。它通过迭代训练多个弱分类器（CART 树），以加法模型的形式逐步优化预测结果，并利用梯度下降法最小化损失函数。在训练过程中，每棵树学习之前模型的残差，最终将所有弱分类器的预测结果加权组合，形成强分类器。

在预测阶段，新样本会依次经过每棵决策树，每棵树输出一个预测值（分类任务为类别得分，回归任务为数值）。模型将这些预测值按训练得到的权重进行加权求和，得到最终预测结果。XGBoost 通过引入正则化项控制模型复杂度，在保证精度的同时有效抑制过拟合，尤其适用于结构化数据的建模任务。

1.2 数据集基本情况回顾

本文依旧沿用Kaggle平台上的加州房价数据集。该数据集包含20,640个样本，共10个特征变量，其中9个为数值型（float64），1个为类别型（object）。

异常值及其处理情况：
缺失值：'total_bedrooms' 有20433个样本，缺失率约 0.99%，用中位数进行填充；
极端值：'median_income'、'total_rooms'、'total_bedrooms'、'population'及'households'存在低于2.5%的极端值，因此采用winsorize进行缩尾处理。

特征间相关性情况：

• longitude 与 latitude：相关系数 - 0.92，极强负相关（p<0.001），符合地理空间规律，经纬度呈明显反向关联。
• total_rooms 与 total_bedrooms：相关系数 0.92，极强正相关（p<0.001），总房间数多的区域，总卧室数通常也多。
• population 与 total_rooms/total_bedrooms：相关系数 0.84/0.87，极强正相关（p<0.001），人口越多，对居住空间需求越大，总房间数、总卧室数通常越多。
• households 与 total_rooms/total_bedrooms：相关系数 0.91/0.97，极强正相关（p<0.001），家庭户数越多，所需的独立居住单元越多，总房间数、总卧室数随之增加。
• population 与 households：相关系数 0.91，极强正相关（p<0.001），家庭由人口组成，家庭户数越多，总人口数通常越多。
• median_income 与 median_house_value：相关系数 0.69，较强正相关（p<0.001），收入越高的区域，房屋价值通常越高。

2. 数据准备

2.1 特征构造

由于total_rooms、total_bedrooms、population和households间均有极强的正相关性，因此为了减少相关性对模型的干扰，创建交互特征。

# 每人平均房间数
df['rooms_per_person'] = df['total_rooms'] / df['population'] 
# 卧室占比 
df['bedrooms_per_room'] = df['total_bedrooms'] / df['total_rooms'] 
# 户均人数 
df['people_per_household'] = df['population'] / df['households'] 

df['income_squared'] = df['median_income'] **2

rooms_per_person：直接量化人均居住空间，是衡量居住舒适度与拥挤程度的客观指标。

bedrooms_per_room：通过卧室占比反映房屋的功能定位。

people_per_household（：推断家庭构成与潜在住房需求的变量。

income_squared（经济非线性特征）：旨在捕捉支付能力与房价之间的非线性规律。

2.2  数据准备

由于该特征为分类变量，因此采用独热编码将其转换为多个二元指示变量，以供模型直接使用。

df = pd.get_dummies(df, columns=['ocean_proximity'], prefix='ocean', drop_first=False)
df = df.rename(columns={'ocean_<1H OCEAN': 'ocean_1H_OCEAN'})

	ocean_1H_OCEAN	ocean_INLAND	ocean_ISLAND	ocean_NEAR BAY	ocean_NEAR OCEAN
0	False	False	False	True	False
1	False	False	False	True	False
2	False	False	False	True	False
3	False	False	False	True	False
4	False	False	False	True	False

拆分数据集：

# 目标变量是 median_house_value
X = df.drop('median_house_value', axis=1)
y = df['median_house_value']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

3. XGBOOST模型

3.1 模型搭建

#搭建模型
model = xgb.XGBRegressor(
    objective='reg:squarederror',  # 回归任务，平方误差损失
    missing=np.nan,  # 启用XGBoost原生缺失值处理
    random_state=42,  # 固定随机种子，保证可复现
    tree_method='hist',  # 高效的直方图算法，适合大数据
    n_jobs=-1  # 并行计算，加速训练
)

构建参数字典param_grid，明确各待优化参数的候选值列表，以此定义网格搜索的参数空间。结合交叉验证策略，对 XGBoost 模型超参数实施自动化调优 —— 通过遍历所有参数组合并验证性能，最终筛选出最优配置，实现模型效能的精准提升。

# 定义待搜索的参数网格
param_grid = {
    'max_depth': [3,4, 5],          # 候选值：树的最大深度（控制过拟合）
    'learning_rate': [0.05, 0.1], # 候选值：学习率（控制步长）
    'n_estimators': [500,1000],  # 候选值：树的数量（模型复杂度）
    'subsample': [0.8, 0.9],           # 候选值：样本采样率（降低过拟合）
    'colsample_bytree': [0.8],     # 候选值：特征采样率（降低过拟合）
    'reg_alpha': [0, 0.5, 1]
}

#  执行网格搜索，找到最优参数和最优模型
grid_search = GridSearchCV(
    estimator=model,    # 传入基础模型框架
    param_grid=param_grid,   # 传入待搜索的参数网格
    cv=5,                    # 5折交叉验证
    scoring='neg_mean_squared_error',  # 评估指标（回归用负MSE）
    n_jobs=-1                # 并行计算加速搜索
)

# 训练所有参数组合（这一步才是“激活”不同参数的模型并评估）
grid_search.fit(X_train, y_train)

# 最终的“最优模型”（已用最优参数配置好，可直接用于预测）
best_xgb_model = grid_search.best_estimator_

• 始化 GridSearchCV 对象，配置基础模型、待搜索参数网格、5 折交叉验证策略，并指定负均方误差（neg_mean_squared_error）为评估标准。
• 调用.fit () 方法启动参数搜索：自动遍历所有参数组合，对每组参数执行交叉验证（训练 + 评估），通过比较平均验证分数，最终筛选出性能最优的参数集。
• 搜索完成后，通过grid_search.best_estimator_即可获取经最优参数配置、并已完成训练的最终模型（best_xgb_model）。该模型整合了参数寻优的结果，可直接用于后续的预测任务与深度分析，无需额外训练，便捷高效。

3.2 特征重要性

分析关键特征的重要性，深入理解模型决策逻辑，提升预测结果的可信度与可靠性，确保其符合业务常识和实际需求。

plt.figure(figsize=(8, 6))
xgb.plot_importance(best_xgb_model, max_num_features=10, importance_type='gain',color = 'maroon')
plt.title('Top 10 Features by Gain')
plt.show()

• ocean_INLAND（内陆地区标识）：重要性最高，表明“是否为内陆地区”是房价的核心决定性因素。清晰反映了远离海岸线的区位属性会显著降低房产价值，凸显出地理区位的首要影响。
• median_income（收入中位数）：作为经济能力的直接体现，其重要性位居前列，强有力地验证了居民支付能力是驱动房价变化的基本经济规律。
• income_squared（收入平方项）：重要性显著，成功捕捉到收入与房价间的非线性关系。这表明在高收入区间，收入的增长对房价的推升作用更为强劲，揭示了财富效应的加速现象。
• people_per_household（户均人口）：重要性较高，表征家庭规模，间接影响对住宅面积和功能的需求。
• rooms_per_person（人均房间数）：直接衡量居住空间的宽敞度与舒适性，是影响房价的关键物理属性。
• ocean_NEAR BAY（近海湾）、ocean_1H_OCEAN（近海一小时圈）与ocean_NEAR OCEAN（近海）共同证实了“亲水”环境对房产的显著溢价效应。
• longitude（经度）与latitude（纬度）的重要性表明，加州房价存在明确的空间分布规律。地理坐标作为区域发展水平、资源禀赋和社区质量的代理变量，共同构成了房价的地理格局。

为探究房屋价值与海洋邻近度的关联性，小提琴图清晰揭示了其间的“空间溢价”分布规律。

plt.figure(figsize=(8, 6))
sns.violinplot(data=df_processed, x='ocean_proximity', y='median_house_value',color='cyan')
plt.title('Relationship between California housing prices and distance to the coast (violin plot)')
plt.xlabel('Distance to the coast')
plt.ylabel('Median price (USD)')
plt.gcf().axes[0].yaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()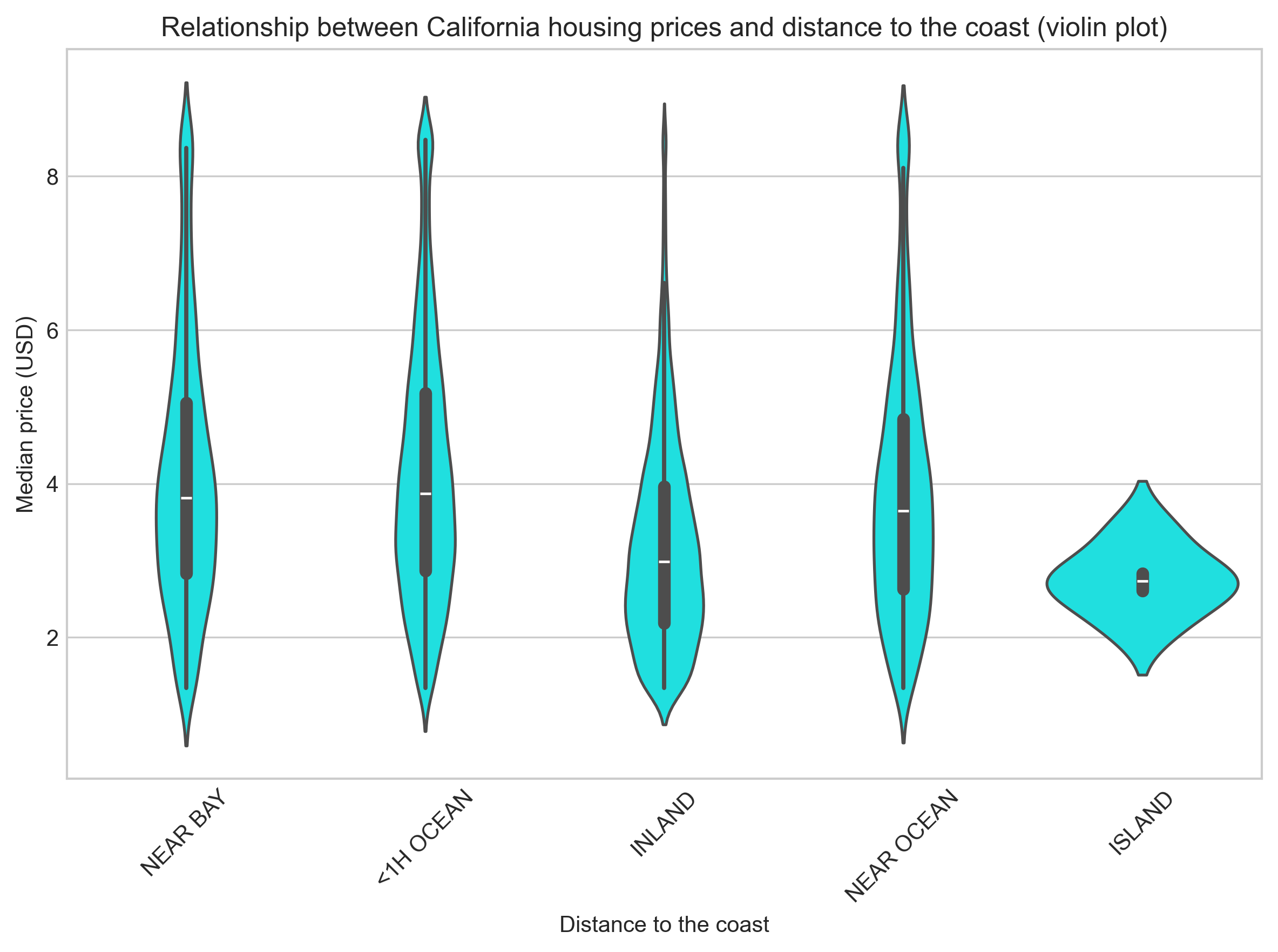

小提琴图显示，加州房价存在显著的地理溢价：临水区域（如近海湾、近海）房价分布呈现高位、离散的形态，表明其价值高且内部差异大；而内陆与岛屿区域则呈现低位、集中的分布，房价普遍偏低。

因此，加州房价是由 “位置好坏、居民收入、住房需求” 共同影响的。这个模型抓住了这些关键因素，不仅能很准地预测房价，更能从地理、经济及市场维度，明确揭示房价形成的内在逻辑。

3.3 模型评估

XGBoost模型的学习曲线如下，横轴记录训练过程中的迭代轮次，纵轴为RMSE（均方根误差），其值越低代表模型预测越精准。其中，蓝色与橙色曲线分别追踪了模型在训练集和测试集上的性能表现。

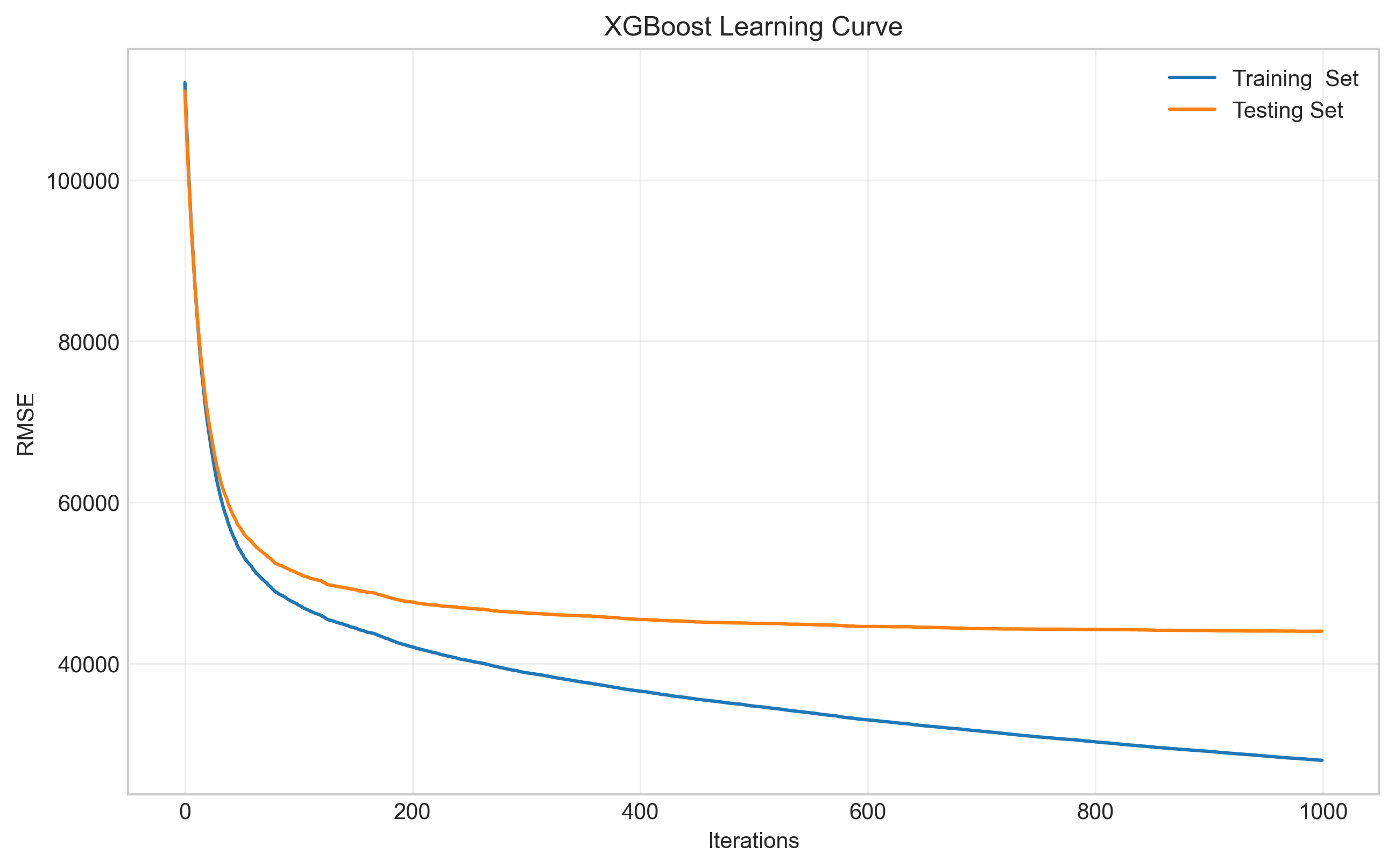
初期学习阶段：在训练初期，两条曲线均呈现快速下降趋势，这表明模型正在有效地从数据中捕捉核心规律，预测能力迅速提升。

收敛与泛化阶段：随着迭代进行，曲线下降速率减缓并最终趋于平稳。训练集误差（蓝线）仍保持缓慢下降，而测试集误差（橙线）则基本稳定在一个较低水平。此模式表明，模型在充分学习的同时，并未对训练数据产生严重过拟合，具备了优秀的泛化能力。

评估指标解释：

MSE (均方误差)：计算预测值与真实值之间差异的平方的平均值。它对较大的误差给予更高的惩罚。

RMSE (均方根误差)：MSE 的平方根。这是最关键的一个指标，因为它将误差恢复到了与原始目标变量（本例中是房价，单位为美元）相同的单位。

MAE (平均绝对误差)：计算预测值与真实值之间绝对差异的平均值。它对所有误差一视同仁。

R² (决定系数)：衡量模型能够解释目标变量方差的比例。它是一个相对指标，越接近 1 越好。

y_pred = best_xgb_model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)  # 均方根误差
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"测试集RMSE：{rmse:.2f}美元")
print(f"测试集MAE：{mae:.2f}美元")
print(f"测试集R²：{r2:.4f}")  

#输出结果：

测试集RMSE：44015.25美元
测试集MAE：29031.52美元
测试集R²：0.8522

模型预测房价与实际值的平均偏差（RMSE）约 4.4 万美元，典型误差（MAE）约 2.9 万美元，整体误差处于可控范围。

R² 达 0.8522，表现优秀，意味着模型能解释 85.22% 的房价波动，证明特征工程和参数调优有效，模型整体拟合效果好，捕捉数据规律的能力强。

模型预测误差在合理范围，且能有效解释房价变化，整体性能良好，可满足基础房价预测需求。

3.4 对比真实值和预测值

plt.figure(figsize=(8, 6))
sns.scatterplot(x=y_test, y=y_pred, alpha=0.6, color='green')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
plt.xlabel('Actual Price ($)')
plt.ylabel('Predicted Price ($)')
plt.title('Actual vs Predicted Prices')
plt.show()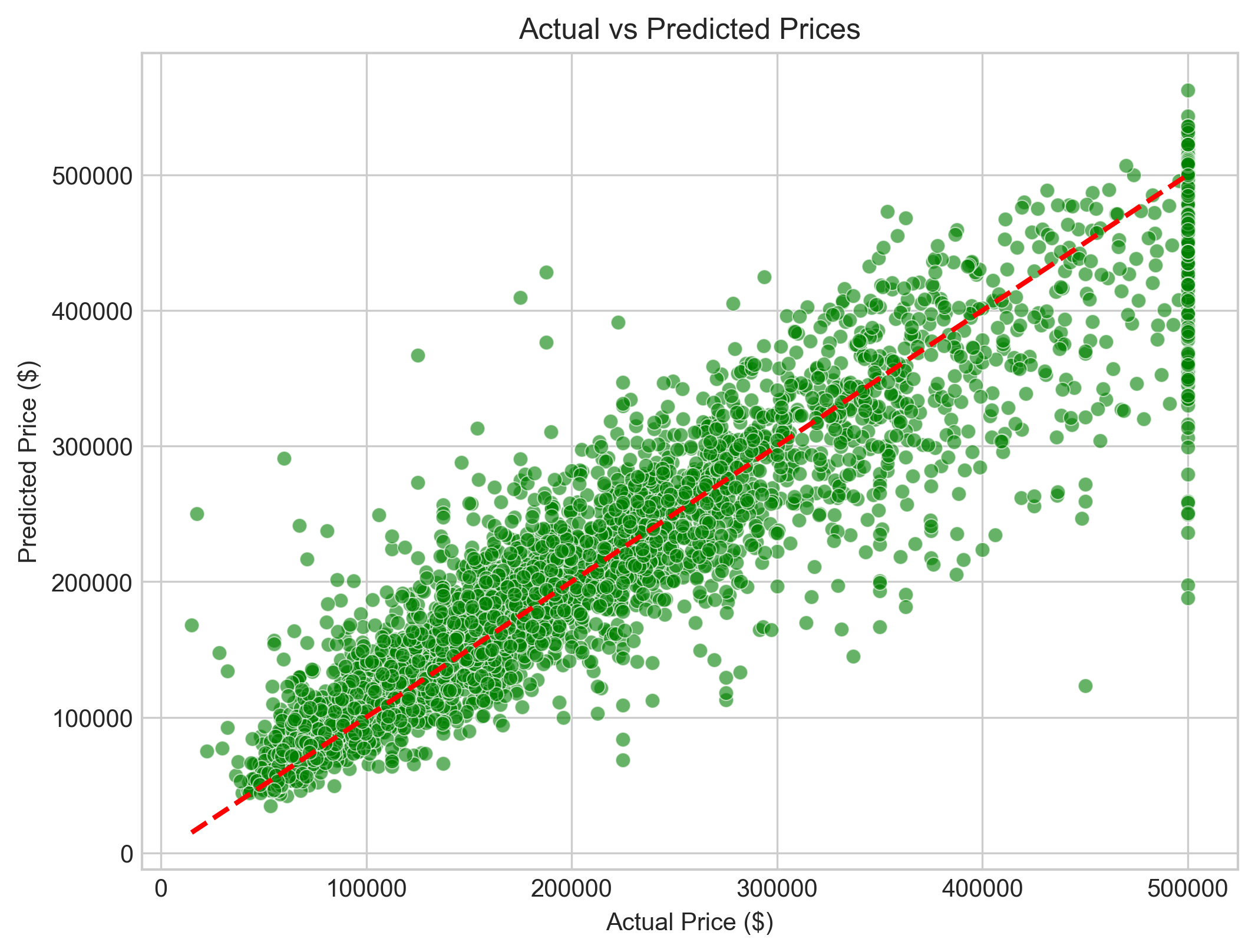

从房价预测对比图可以看出，绿色散点大多紧密分布在红色虚线附近，仅在高价和低价区域出现少量轻微偏离。这表明：模型预测结果与实际房价整体吻合度较高，误差控制在合理范围内，能够准确捕捉房价变化规律，在实际应用中表现出良好的预测可靠性。

---

总结

本文结合加州房价数据及前期预处理成果，构建高性能 XGBoost 回归模型。经严谨特征工程，揭示地理区位（临水溢价）、经济能力（收入非线性推动）、居住属性（空间舒适度）三大房价核心驱动力。模型经网格搜索优化，学习曲线稳健，测试集 R² 达 0.85，泛化良好，既实现精准预测，也为解读房价逻辑、辅助决策提供量化依据。
欢迎指正，感谢您的阅读！