向量数据库调研
查询复杂度主要是哈希函数的计算复杂度和哈希表的遍历复杂度,一般时间复杂度达到O(N^p),其中N是数据库中向量的数量。时间复杂度主要是与K(最近邻数目)、N(向量数目)和D(向量空间维数)相关,因此时间复杂度能够低至O(log N)。预处理时间复杂度为O(N * D),其中N是数据库中向量的数量,D是向量的维度;自定义实现的 HNSW,调整到规模,并支持完整的 CRUD。搜索复杂度为O(N log
向量数据库的优势
|
数据库类型 |
适用场景 |
典型数据库举例 |
|
关系型数据库(RDBMS) |
处理结构化数据,擅长OLTP,如财务、人事管理等。 |
MySQL,Oracle,SQL Server |
|
非关系型数据库(NoSQL) |
存储大量非结构化或半结构化数据,擅长点查,如大数据分析、人工智能等。 |
MongoDB,Redis,Cassandra |
|
对象数据库 |
数据存储结构比较复杂的应用场景 |
Versant Object Database,ObjectStore,ZopeDB |
|
列式数据库 |
需要快速进行按列查询的应用场景,擅长OLTP查询,如数据仓库。 |
HBase,Cassandra,Amazon DynamoDB |
|
图形数据库 |
存储和处理大型图形数据,一般使用GraphQL如社交网络、物联网等场景。 |
Neo4j,ArangoDB,JanusGraph |
|
向量数据库 |
快速处理向量数据的应用场景,擅长算法聚类等,如图像识别、音频处理、自然语言处理等 |
Milvus,Faiss,Hive-Vector-Storage |
|
全文搜索引擎(search db) |
处理全文搜索和日志存储等应用场景 |
Elasticsearch,Apache Solr,Sphinx |
在 db engines rank中,向量数据在最近一段时间得到很强的关注和发展。
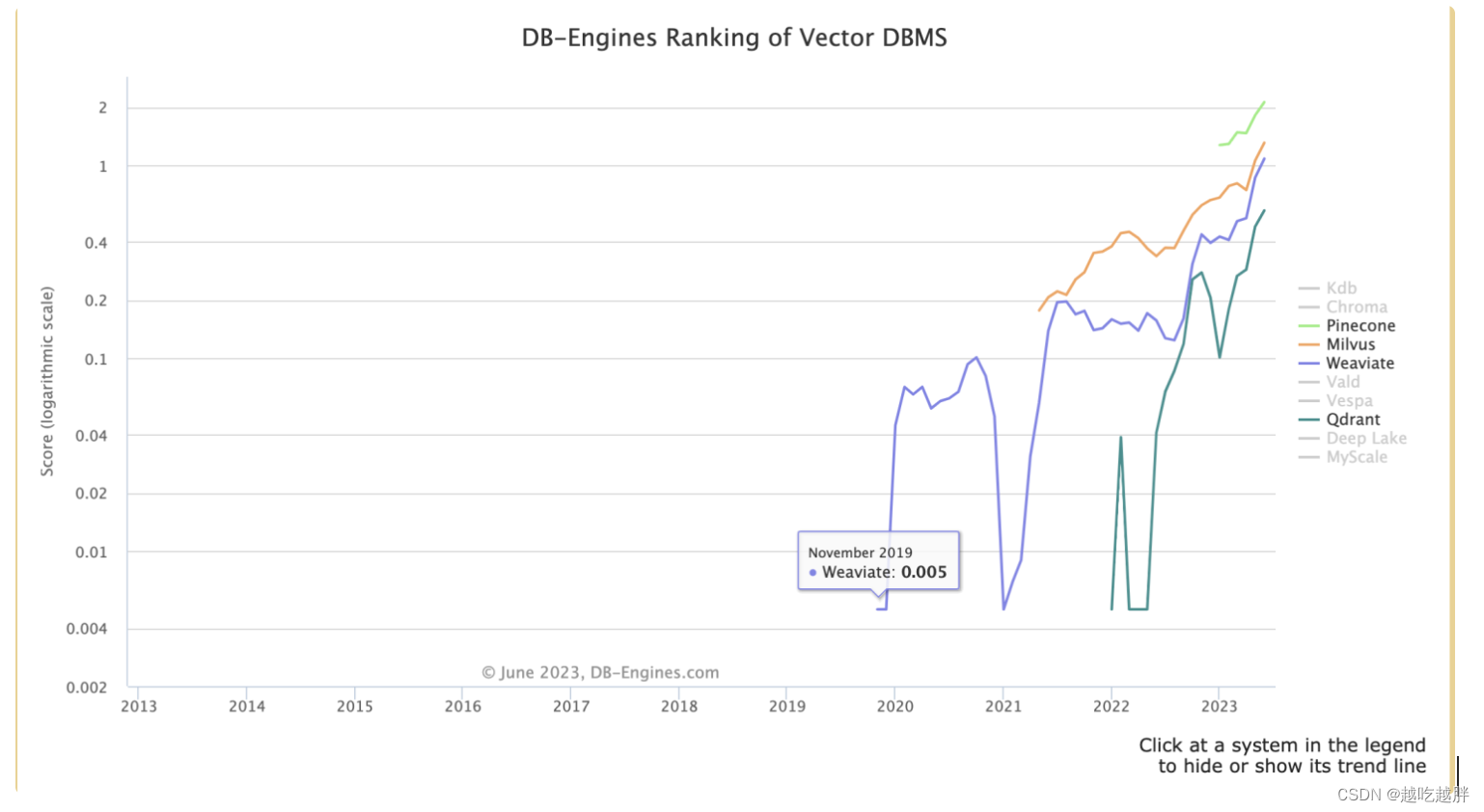
向量数据库横向对比
Milvus、Pinecone、Vespa、Weaviate、Vald、GSI 和 Qdrant
- 价值主张。让整个向量搜索引擎脱颖而出的独特之处是什么?
- 类型。该引擎的通用类型:向量数据库、大数据平台。托管/自托管。
- 架构。高级系统架构,包括分片、插件、可扩展性、硬件细节(如果可用)等方面。
- 算法。这个搜索引擎采用了什么算法来进行相似度/向量搜索,它提供了哪些独特的功能?
- 代码:它是开源的还是闭源的?
|
类型 |
代码 |
算法 |
|
|
自托管 |
开源 |
允许多个基于 ANN 算法的索引:FAISS、ANNOY、HNSW、RNSG。 |
|
|
托管 |
闭源 |
由 FAISS 提供支持的 Exact KNN;ANN 由专有算法提供支持。支持所有主要距离度量:余弦(默认)、点积和欧几里得。 |
|
|
托管/自托管 |
开源 |
HNSW(针对实时CRUD和元数据过滤进行了修改);一套重新排序和密集检索方法。 |
|
|
托管/自托管 |
开源 |
自定义实现的 HNSW,调整到规模,并支持完整的 CRUD。只要能做CRUD ,系统就支持插件ANN算法。 |
|
|
自托管 |
开源 |
基于最快算法:NGT,比很多强算法,如Scann和HNSW都要快。 |
|
|
ES OS的向量搜索硬件后端 |
闭源 |
保持神经散列的汉明空间局部性。 |
|
|
托管/自托管 |
开源 |
Rust 中的自定义HNSW 实现。 |
向量数据库依赖算法的优劣势
|
算法名称 |
算法优势 |
算法劣势 |
复杂度分析 |
|
Exact KNN |
精确性高,可以保证正确性 |
对大型数据集的搜索较慢 |
搜索复杂度为O(N log N),其中N是数据库中向量的数量。对于高维数据和大量数据,复杂度可能会比较高 |
|
LSH |
可以在大型数据集中实现快速近似KNN搜索 |
近似性较差,可能会导致搜索结果不够准确 |
查询复杂度主要是哈希函数的计算复杂度和哈希表的遍历复杂度,一般时间复杂度达到O(N^p),其中N是数据库中向量的数量。 |
|
Scann |
快速和可扩展,特别适合大量高维向量的搜索 |
相比于精确KNN和其他近似KNN算法,精度可能会有所降低 |
预处理时间复杂度为O(N * D),其中N是数据库中向量的数量,D是向量的维度;查询复杂度为O(log N)。 |
|
KD树 |
计算快速,适合高维度空间的KNN搜索 |
对于包含稀疏数据的向量,性能可能会受到影响 |
预处理时间复杂度为O(N * log N),其中N是数据库中向量的数量;查询复杂度为O(log N)。 |
|
HNSW |
可以在大型高维数据集中实现快速近似KNN搜索,且精度较高 |
查询速度较慢(不如LSH和SCANN) |
构建时间复杂度为O(N * log N),其中N是数据库中向量的数量;查询复杂度为O(log N)。 |
|
RNSG |
较快的最近邻搜索速度,且搜索结果较为准确 |
不适用于非欧几里得空间 |
时间复杂度主要是与K(最近邻数目)、N(向量数目)和D(向量空间维数)相关,因此时间复杂度能够低至O(log N)。 |
向量数据库分析
milvus
架构实现:Milvus 实现了四层:接入层、协调服务、工作节点和存储。这些层是独立的,以实现更好的可扩展性和灾难恢复。
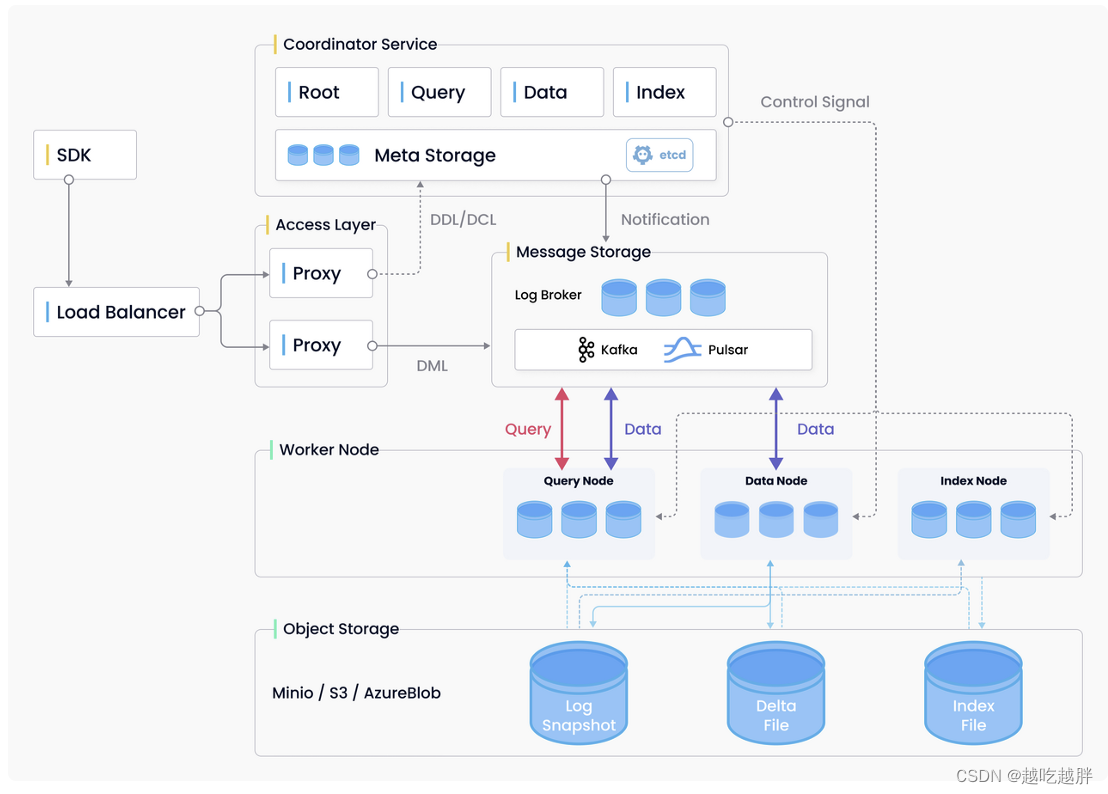
产品优势:
- 支持私有化部署
- 多版本:单机版(standalone)、集群版(cluster),支持部署在CPU和GPU上,弹性可扩展。
- 易运维:采用云原生架构,使用docker和k8s能够快速安装和运维。
- 实现场景多:能快速实现图搜图、语音搜索语音、文搜文。
参考资料
链接

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)