无监督学习与有监督学习的本质区别是什么_无监督学习之数据降维
无监督学习有一个特别的作用就是给高维数据降维,比如一个MNIST的图片,1*28*28=784维数据,难以有直观的理解,因为人类视觉容易理解的只有1维线,2维面和3维体,这时候无监督学习就有了用武之地,还有一个特点就是无监督学习不需要数据标签,下面来一个简单的例子准备数据准备两组数据,10维的,第一组产生3维的随机向量,然后使用3维数据生成10维数据,第二组直接就是10维的随机向量两组数据产生逻辑
无监督学习有一个特别的作用就是给高维数据降维,比如一个MNIST的图片,1*28*28=784维数据,难以有直观的理解,因为人类视觉容易理解的只有1维线,2维面和3维体,这时候无监督学习就有了用武之地,还有一个特点就是无监督学习不需要数据标签,下面来一个简单的例子
准备数据
准备两组数据,10维的,第一组产生3维的随机向量,然后使用3维数据生成10维数据,第二组直接就是10维的随机向量

两组数据产生逻辑
这里解释一下,实际第一组数据就是3维的,因为3维以外的其他7维都是这3维生成的,即都是相关的,那么理论上来说,这组数据应该可以在3维空间表达出来,现在我们来降维
降维网络

6层降维网络
重建网络
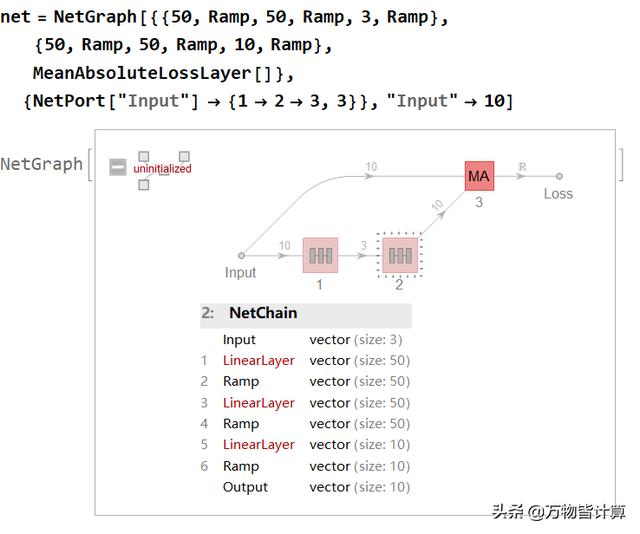
重建网络
损失函数
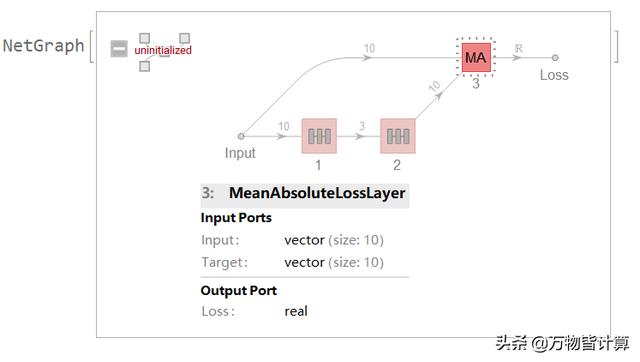
损失函数
基本原理:先对输入数据进行降维,这里会降到3维,然后使用这个3维数据重建原来的数据,再和原来的数据进行对比计算损失函数,如果效果好的话,理论上来说,10维数据就和降维后的3维数据相关,不然的话就不可能由3维数据重建得到
训练网络
训练容易陷入局部最优解,多训练几次,保留损失最低的结果
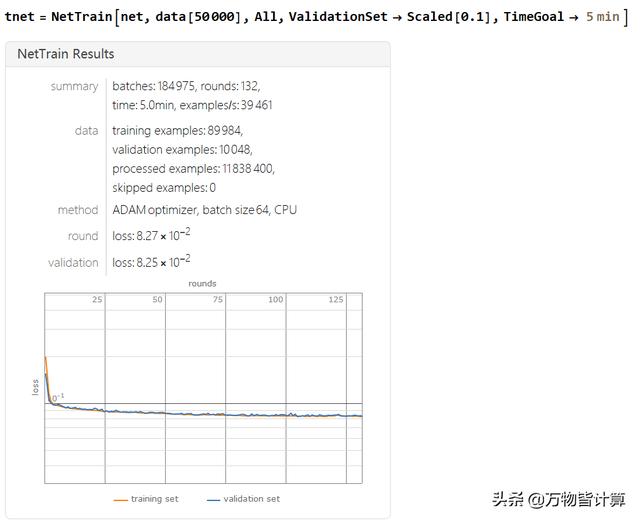
训练结果
提取网路

降维网路,重建网络
评估网络质量

网络评估
两个类别都生成100个数据,进行降维重建,和原来的数据计算差异,差异越小,网络质量越高
降维数据可视化
10维数据降维到3维,就可以可视化了
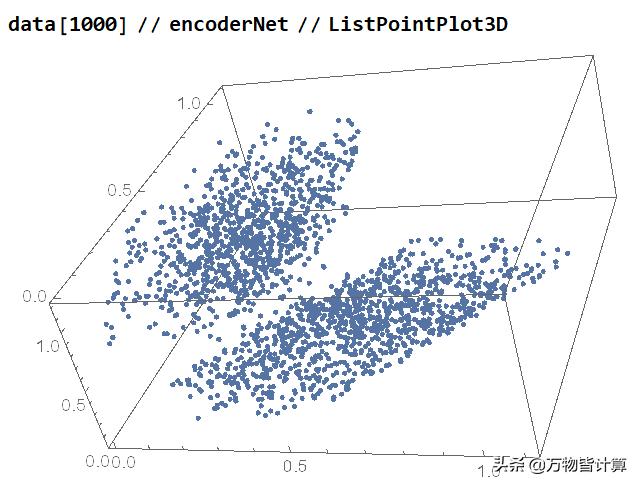
数据3维可视化
可以看到空间中的3维点分为2部分,如果我们按照原来的数据着色的话,就可以看出来,两个类型的数据通过可视化就已经可以肉眼进行分类了
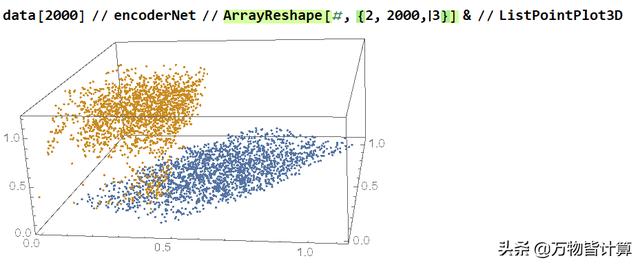
按照生成规则着色
在我们不知道数据到底有没有特征或者特征分明的分类的时候,做数据降维可以帮助我们进行数据的聚类分析

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容








所有评论(0)