【计算机图形学】实验二:曲线拟合
(1)给定四个已知点P1—P4,以此作为控制顶点绘制一段三次Bezier曲线。(2)给定四个已知点P1—P4,以此作为曲线上的点绘制一段三次Bezier曲线。给定六个已知点P1—P6,以此作为控制顶点绘制一条三次B样条曲线。Visual Studio 2019图形学实验程序框架Windows11系统对于问题1(1),三次Bezier曲线的矩阵表示形式如下:Q(t)=(t3t2t1)(−13−313
写在前面
效果演示移步视频
https://www.bilibili.com/video/BV1ah4y177dL
目录
1. 实验内容
1. 绘制三次Bezier曲线
(1)给定四个已知点P1—P4,以此作为控制顶点绘制一段三次Bezier曲线。
(2)给定四个已知点P1—P4,以此作为曲线上的点绘制一段三次Bezier曲线。
2.绘制三次B样条曲线
给定六个已知点P1—P6,以此作为控制顶点绘制一条三次B样条曲线。
2. 实验环境
Visual Studio 2019
图形学实验程序框架
Windows11系统
3. 问题分析
3.1问题1(1)
对于问题1(1),三次Bezier曲线的矩阵表示形式如下:
Q ( t ) = ( t 3 t 2 t 1 ) ( − 1 3 − 3 1 3 − 6 3 0 − 3 3 0 0 1 0 0 0 ) ( P 0 P 1 P 2 P 3 ) ( 0 ≤ t ≤ 1 ) Q(t)=\begin{pmatrix}t^3&t^2&t&1\end{pmatrix}\begin{pmatrix}-1&3&-3&1\\3&-6&3&0\\-3&3&0&0\\1&0&0&0\end{pmatrix}\begin{pmatrix}P_0\\P_1\\P_2\\P_3\end{pmatrix}(0\le t\le 1) Q(t)=(t3t2t1)
−13−313−630−33001000
P0P1P2P3
(0≤t≤1)
其中, P 3 P_3 P3, P 2 P_2 P2, P 1 P_1 P1, P 0 P_0 P0分别为4个控制点坐标值。 Q ( t ) Q(t) Q(t)为曲线上点的坐标值。 t t t为参数。
曲线的参数式为:
{ x ( t ) = a x t 3 + b x t 2 + c x t + d x y ( t ) = a y t 3 + b y t 2 + c y t + d y ( 0 ≤ t ≤ 1 ) . ( 1 ) \begin{cases}x(t)=a_xt^3+b_xt^2+c_xt+d_x\\y(t)=a_yt^3+b_yt^2+c_yt+d_y\end{cases}(0\le t\le 1).(1) {x(t)=axt3+bxt2+cxt+dxy(t)=ayt3+byt2+cyt+dy(0≤t≤1).(1)
式中系数分别为:
a x = − x 0 + 3 x 1 − 3 x 2 + x 3 a y = − y 0 + 3 y 1 − 3 y 2 + y 3 b x = 3 x 0 − 6 x 1 + 3 x 2 b y = 3 y 0 − 6 y 1 + 3 y 2 c x = − 3 x 0 + 3 x 1 c y = − 3 y 0 + 3 y 1 d x = x 0 d y = y 0 . ( 2 ) \begin{matrix} a_x=-x_0+3x_1-3x_2+x_3&a_y=-y_0+3y_1-3y_2+y_3\\ b_x=3x_0-6x_1+3x_2&b_y=3y_0-6y_1+3y_2\\ c_x=-3x_0+3x_1&c_y=-3y_0+3y_1\\ d_x=x_0&d_y=y_0 \end{matrix}.(2) ax=−x0+3x1−3x2+x3bx=3x0−6x1+3x2cx=−3x0+3x1dx=x0ay=−y0+3y1−3y2+y3by=3y0−6y1+3y2cy=−3y0+3y1dy=y0.(2)
在设计程序时,只需将控制点 P i ( i = 0 , 1 , 2 , 3 ) P_i(i=0,1,2,3) Pi(i=0,1,2,3)的坐标 ( x i , y i ) (x_i,y_i) (xi,yi)代入 ( 2 ) (2) (2)式解得 a x , b x , c x , d x a_x,b_x,c_x,d_x ax,bx,cx,dx与 a y , b y , c y , d y a_y,b_y,c_y,d_y ay,by,cy,dy,再将求解得到的值代入 ( 1 ) (1) (1)即可。
3.2问题1(2)
对于问题1(2),已知曲线上4个点,画出穿过这4个点的三次Bezier曲线。线上4个点对应参变量 t t t的取值。其中,第 0 0 0号点对应的 t = 0 t=0 t=0,第 3 3 3号点对应的 t = 1 t=1 t=1,第 1 1 1号点与第 2 2 2号点对应的取值可以自定。在本文中,取第 1 1 1号点对应的 t = 0.25 t=0.25 t=0.25,取第 2 2 2号点对应的 t = 0.5 t=0.5 t=0.5。
已知曲线上四个点 Q ( 0 ) , Q ( t 1 ) , Q ( t 2 ) , Q ( 1 ) Q(0),Q(t_1),Q(t_2),Q(1) Q(0),Q(t1),Q(t2),Q(1),其中 0 ≤ t 1 ≤ t 2 ≤ 1 0\le t_1 \le t_2 \le 1 0≤t1≤t2≤1,将其代入 ( 1 ) (1) (1)式,得到方程组:
x ( 0 ) = d x x ( t 1 ) = a x t 1 3 + b x t 1 2 + c x t 1 + d x x ( t 2 ) = a x t 2 3 + b x t 2 2 + c x t 2 + d x x ( 1 ) = a x + b x + c x + d x . ( 3 ) \begin{matrix} x(0)=d_x\\ x(t_1)=a_xt_1^3+b_xt_1^2+c_xt_1+d_x\\ x(t_2)=a_xt_2^3+b_xt_2^2+c_xt_2+d_x\\ x(1)=a_x+b_x+c_x+d_x \end{matrix}.(3) x(0)=dxx(t1)=axt13+bxt12+cxt1+dxx(t2)=axt23+bxt22+cxt2+dxx(1)=ax+bx+cx+dx.(3)
其中, x ( t i ) x(t_i) x(ti)为曲线上已知点的横坐标,为已知量。将$(3)式写成矩阵形式如下:
( 0 0 0 1 t 1 3 t 1 2 t 1 1 t 2 3 t 2 2 t 2 1 1 1 1 1 ) ( a x b x c x d x ) = ( x ( 0 ) x ( t 1 ) x ( t 2 ) x ( 1 ) ) . ( 4 ) \begin{pmatrix} 0&0&0&1\\ t_1^3&t_1^2&t_1&1\\ t_2^3&t_2^2&t_2&1\\ 1&1&1&1 \end{pmatrix} \begin{pmatrix} a_x\\b_x\\c_x\\d_x \end{pmatrix}= \begin{pmatrix} x(0)\\x(t_1)\\x(t_2)\\x(1) \end{pmatrix}.(4)
0t13t2310t12t2210t1t211111
axbxcxdx
=
x(0)x(t1)x(t2)x(1)
.(4)
对 ( 4 ) (4) (4)式,左乘矩阵 ( 0 0 0 1 t 1 3 t 1 2 t 1 1 t 2 3 t 2 2 t 2 1 1 1 1 1 ) \begin{pmatrix}0&0&0&1\\t_1^3&t_1^2&t_1&1\\t_2^3&t_2^2&t_2&1\\1&1&1&1\end{pmatrix}
0t13t2310t12t2210t1t211111
的逆矩阵,即可解得 ( a x b x c x d x ) T \begin{pmatrix}a_x&b_x&c_x&d_x\end{pmatrix}^T (axbxcxdx)T
( a x b x c x d x ) = ( 0 0 0 1 t 1 3 t 1 2 t 1 1 t 2 3 t 2 2 t 2 1 1 1 1 1 ) − 1 ( x ( 0 ) x ( t 1 ) x ( t 2 ) x ( 1 ) ) . ( 5 ) \begin{pmatrix} a_x\\b_x\\c_x\\d_x \end{pmatrix}= \begin{pmatrix} 0&0&0&1\\ t_1^3&t_1^2&t_1&1\\ t_2^3&t_2^2&t_2&1\\ 1&1&1&1 \end{pmatrix}^{-1} \begin{pmatrix} x(0)\\x(t_1)\\x(t_2)\\x(1) \end{pmatrix}.(5)
axbxcxdx
=
0t13t2310t12t2210t1t211111
−1
x(0)x(t1)x(t2)x(1)
.(5)
对 ( a y b y c y d y ) T \begin{pmatrix}a_y&b_y&c_y&d_y\end{pmatrix}^T (aybycydy)T,同理:
( a y b y c y d y ) = ( 0 0 0 1 t 1 3 t 1 2 t 1 1 t 2 3 t 2 2 t 2 1 1 1 1 1 ) − 1 ( y ( 0 ) y ( t 1 ) y ( t 2 ) y ( 1 ) ) . ( 6 ) \begin{pmatrix} a_y\\b_y\\c_y\\d_y \end{pmatrix}= \begin{pmatrix} 0&0&0&1\\ t_1^3&t_1^2&t_1&1\\ t_2^3&t_2^2&t_2&1\\ 1&1&1&1 \end{pmatrix}^{-1} \begin{pmatrix} y(0)\\y(t_1)\\y(t_2)\\y(1) \end{pmatrix}.(6)
aybycydy
=
0t13t2310t12t2210t1t211111
−1
y(0)y(t1)y(t2)y(1)
.(6)
将根据式 ( 5 ) (5) (5)与 ( 6 ) (6) (6)式解得 ( a x b x c x d x ) T \begin{pmatrix}a_x&b_x&c_x&d_x\end{pmatrix}^T (axbxcxdx)T的 ( a y b y c y d y ) T \begin{pmatrix}a_y&b_y&c_y&d_y\end{pmatrix}^T (aybycydy)T与代入 ( 1 ) (1) (1)式,即可绘制出满足问题1(2)的Bezier曲线。
根据已知的需要穿过的曲线上四个点 Q ( 0 ) , Q ( t 1 ) , Q ( t 2 ) , Q ( 1 ) Q(0),Q(t_1),Q(t_2),Q(1) Q(0),Q(t1),Q(t2),Q(1),还可以反推控制点。其中,控制点 P 0 P_0 P0与 P 3 P_3 P3已知, P 1 P_1 P1与 P 2 P_2 P2未知。
Q 1 = ( t 1 3 t 1 2 t 1 1 ) ( − 1 3 − 3 1 3 − 6 3 0 − 3 3 0 0 1 0 0 0 ) ( P 0 P 1 P 2 P 3 ) = ( a 3 a 2 a 1 a 0 ) ( P 0 P 1 P 2 P 3 ) ( 7 ) Q_1= \begin{pmatrix} t_1^3&t_1^2&t_1&1 \end{pmatrix} \begin{pmatrix} -1&3&-3&1\\ 3&-6&3&0\\ -3&3&0&0\\ 1&0&0&0 \end{pmatrix} \begin{pmatrix} P_0\\P_1\\P_2\\P_3 \end{pmatrix}= \begin{pmatrix} a_3&a_2&a_1&a_0 \end{pmatrix} \begin{pmatrix} P_0\\P_1\\P_2\\P_3 \end{pmatrix}(7) Q1=(t13t12t11)
−13−313−630−33001000
P0P1P2P3
=(a3a2a1a0)
P0P1P2P3
(7)
Q 1 = ( t 2 3 t 2 2 t 2 1 ) ( − 1 3 − 3 1 3 − 6 3 0 − 3 3 0 0 1 0 0 0 ) ( P 0 P 1 P 2 P 3 ) = ( b 3 b 2 b 1 b 0 ) ( P 0 P 1 P 2 P 3 ) ( 8 ) Q_1= \begin{pmatrix} t_2^3&t_2^2&t_2&1 \end{pmatrix} \begin{pmatrix} -1&3&-3&1\\ 3&-6&3&0\\ -3&3&0&0\\ 1&0&0&0 \end{pmatrix} \begin{pmatrix} P_0\\P_1\\P_2\\P_3 \end{pmatrix}= \begin{pmatrix} b_3&b_2&b_1&b_0 \end{pmatrix} \begin{pmatrix} P_0\\P_1\\P_2\\P_3 \end{pmatrix}(8) Q1=(t23t22t21)
−13−313−630−33001000
P0P1P2P3
=(b3b2b1b0)
P0P1P2P3
(8)
联立 ( 7 ) ( 8 ) (7)(8) (7)(8)式,可得:
( a 2 a 1 b 2 b 1 ) ( P 1 P 2 ) = ( Q 1 − a 3 P 0 − a 0 P 3 Q 2 − b 3 P 0 − b 0 P 3 ) ( 9 ) \begin{pmatrix} a_2&a_1\\ b_2&b_1 \end{pmatrix} \begin{pmatrix} P_1\\P_2 \end{pmatrix}= \begin{pmatrix} Q_1-a_3P_0-a_0P_3\\Q_2-b_3P_0-b_0P_3 \end{pmatrix}(9) (a2b2a1b1)(P1P2)=(Q1−a3P0−a0P3Q2−b3P0−b0P3)(9)
解得:
( P 1 P 2 ) = ( a 2 a 1 b 2 b 1 ) − 1 ( Q 1 − a 3 P 0 − a 0 P 3 Q 2 − b 3 P 0 − b 0 P 3 ) ( 10 ) \begin{pmatrix} P_1\\P_2 \end{pmatrix}= \begin{pmatrix} a_2&a_1\\ b_2&b_1 \end{pmatrix}^{-1} \begin{pmatrix} Q_1-a_3P_0-a_0P_3\\Q_2-b_3P_0-b_0P_3 \end{pmatrix}(10) (P1P2)=(a2b2a1b1)−1(Q1−a3P0−a0P3Q2−b3P0−b0P3)(10)
( 10 ) (10) (10)式即根据曲线通过的点反推了控制点 P 1 P_1 P1和 P 2 P_2 P2。
3.3问题2
对于问题2,三次B样条曲线的矩阵表示形式如下:
Q ( t ) = ( t 3 t 2 t 1 ) 1 6 ( − 1 3 − 3 1 3 − 6 3 0 − 3 0 3 0 1 4 1 0 ) ( P 0 P 1 P 2 P 3 ) ( 0 ≤ t ≤ 1 ) . ( 11 ) Q(t)= \begin{pmatrix} t^3&t^2&t&1 \end{pmatrix} \frac16 \begin{pmatrix} -1&3&-3&1\\ 3&-6&3&0\\ -3&0&3&0\\ 1&4&1&0 \end{pmatrix} \begin{pmatrix} P_0\\P_1\\P_2\\P_3 \end{pmatrix} (0\le t \le 1).(11) Q(t)=(t3t2t1)61
−13−313−604−33311000
P0P1P2P3
(0≤t≤1).(11)
分解后的参数式为:
{ x ( t ) = a x t 3 + b x t 2 + c x t + d x y ( t ) = a y t 3 + b y t 2 + c y t + d y ( 0 ≤ t ≤ 1 ) ( 12 ) \begin{cases} x(t)=a_xt^3+b_xt^2+c_xt+d_x\\ y(t)=a_yt^3+b_yt^2+c_yt+d_y \end{cases}(0\le t \le 1)(12) {x(t)=axt3+bxt2+cxt+dxy(t)=ayt3+byt2+cyt+dy(0≤t≤1)(12)
式中系数分别为:
a x = − ( x 0 − 3 x 1 + 3 x 2 − x 3 ) / 6 a y = − ( y 0 − 3 y 1 + 3 y 2 − y 3 ) / 6 b x = ( x 0 − 2 x 1 + x 2 ) / 2 b y = ( y 0 − 2 y 1 + y 2 ) / 2 c x = − ( x 0 − x 2 ) / 2 c y = − ( y 0 − y 2 ) / 2 d x = ( x 0 + 4 x 1 + x 2 ) / 6 d y = ( y 0 + 4 y 1 + y 2 ) / 6 \begin{matrix} a_x=-(x_0-3x_1+3x_2-x_3)/6&a_y=-(y_0-3y_1+3y_2-y_3)/6\\ b_x=(x_0-2x_1+x_2)/2&b_y=(y_0-2y_1+y_2)/2\\ c_x=-(x_0-x_2)/2&c_y=-(y_0-y_2)/2\\ d_x=(x_0+4x_1+x_2)/6&d_y=(y_0+4y_1+y_2)/6 \end{matrix} ax=−(x0−3x1+3x2−x3)/6bx=(x0−2x1+x2)/2cx=−(x0−x2)/2dx=(x0+4x1+x2)/6ay=−(y0−3y1+3y2−y3)/6by=(y0−2y1+y2)/2cy=−(y0−y2)/2dy=(y0+4y1+y2)/6
一段三次B样条曲线需要4个控制点。但在已有三次B样条曲线的情况下,可以额外增加一个控制点,即可相应地增加一段B样条曲线,自然地能达到 C 2 C_2 C2连续。
4. 算法设计
4.1问题1(1)
正如3.1所分析,算法的流程如下:
1.计算求解系数 a x , b x , c x , d x a_x,b_x,c_x,d_x ax,bx,cx,dx与 a y , b y , c y , d y a_y,b_y,c_y,d_y ay,by,cy,dy。
2.从 t = 0 t=0 t=0开始,设置步长 t = 0.001 t=0.001 t=0.001,对于每一个步长 t t t值,按 ( 14 ) (14) (14)式绘制曲线。
{ x ( t ) = a x t 3 + b x t 2 + c x t + d x y ( t ) = a y t 3 + b y t 2 + c y t + d y ( 0 ≤ t ≤ 1 ) ( 14 ) \begin{cases} x(t)=a_xt^3+b_xt^2+c_xt+d_x\\ y(t)=a_yt^3+b_yt^2+c_yt+d_y \end{cases}(0\le t \le 1)(14) {x(t)=axt3+bxt2+cxt+dxy(t)=ayt3+byt2+cyt+dy(0≤t≤1)(14)
3.循环第2步,直到 t = 1 t=1 t=1时结束。
算法的流程图如下: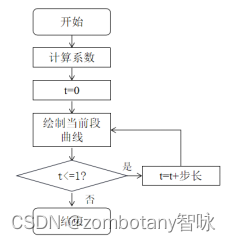
4.2问题2
正如章节3.2分析,算法的流程如下:
1.根据 ( 5 ) ( 6 ) (5)(6) (5)(6)式,求解 a x , b x , c x , d x a_x,b_x,c_x,d_x ax,bx,cx,dx与 a y , b y , c y , d y a_y,b_y,c_y,d_y ay,by,cy,dy。
2.从 t = 0 t=0 t=0开始,设置步长 t = 0.001 t=0.001 t=0.001,对于每一个步长 t t t值,按 ( 15 ) (15) (15)式绘制曲线。
{ x ( t ) = a x t 3 + b x t 2 + c x t + d x y ( t ) = a y t 3 + b y t 2 + c y t + d y ( 0 ≤ t ≤ 1 ) ( 15 ) \begin{cases} x(t)=a_xt^3+b_xt^2+c_xt+d_x\\ y(t)=a_yt^3+b_yt^2+c_yt+d_y \end{cases}(0\le t\le 1)(15) {x(t)=axt3+bxt2+cxt+dxy(t)=ayt3+byt2+cyt+dy(0≤t≤1)(15)
3.循环第2步,直到 t = 1 t=1 t=1时结束。
4.根据 ( 10 ) (10) (10)式反推控制点,并将4个控制点连结成线。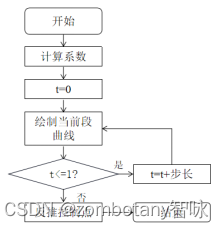
4.3问题3
正如章节3.3所分析,算法的流程如下:
1.取 i = 0 i=0 i=0。
2.根据 P i , P i + 1 , P i + 2 , P i + 3 P_i,P_{i+1},P_{i+2},P_{i+3} Pi,Pi+1,Pi+2,Pi+3这四个控制点计算参数 a x , b x , c x , d x a_x,b_x,c_x,d_x ax,bx,cx,dx与 a y , b y , c y , d y a_y,b_y,c_y,d_y ay,by,cy,dy。
3.从 t = 0 t=0 t=0开始,设置步长 t = 0.001 t=0.001 t=0.001,对于每一个步长 t t t值,按式 ( 16 ) (16) (16)绘制曲线。
{ x ( t ) = a x t 3 + b x t 2 + c x t + d x y ( t ) = a y t 3 + b y t 2 + c y t + d y ( 0 ≤ t ≤ 1 ) ( 16 ) \begin{cases} x(t)=a_xt^3+b_xt^2+c_xt+d_x\\ y(t)=a_yt^3+b_yt^2+c_yt+d_y \end{cases}(0\le t\le 1)(16) {x(t)=axt3+bxt2+cxt+dxy(t)=ayt3+byt2+cyt+dy(0≤t≤1)(16)
4.循环第3步,直到 t = 1 t=1 t=1时结束。
5. i ← i + 1 i\leftarrow i+1 i←i+1循环第2步,直到遍历完所有控制点。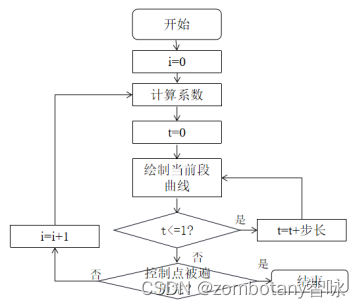
5. 源代码
5.1 Bezier1
//以已知的四个点为控制点绘制Bezier曲线
//p:已知的四个控制点
void CDiamondView::DrawBezier1(POINT p[4])
{
InvalidateRect(NULL);//强制清屏
UpdateWindow();
CDC* pDC = GetDC();
CPen newPen, * oldPen;
newPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 0));
oldPen = pDC->SelectObject(&newPen);
pDC->Polyline(p, 4);
pDC->SelectObject(oldPen);
CPen newPen2;
newPen2.CreatePen(PS_SOLID, 2, RGB(255, 0, 0));
oldPen = pDC->SelectObject(&newPen2);
double ax = -p[0].x + 3 * p[1].x - 3 * p[2].x + p[3].x;
double ay = -p[0].y + 3 * p[1].y - 3 * p[2].y + p[3].y;
double bx = 3 * p[0].x - 6 * p[1].x + 3 * p[2].x;
double by = 3 * p[0].y - 6 * p[1].y + 3 * p[2].y;
double cx = -3 * p[0].x + 3 * p[1].x;
double cy = -3 * p[0].y + 3 * p[1].y;
double dx = p[0].x;
double dy = p[0].y;
pDC->MoveTo(p[0].x, p[0].y);
for (double t = 0; t <= 1; t = t + 0.001) {
int xt = ax * t * t * t + bx * t * t + cx * t + dx;
int yt = ay * t * t * t + by * t * t + cy * t + dy;
pDC->LineTo(xt, yt);
// Sleep(10);
}
pDC->SelectObject(oldPen);
}
5.2 Bezier2
//以已知的四个点为Bezier曲线上的点来绘制Bezier曲线
//p:已知的四个点
void CDiamondView::DrawBezier2(POINT p[4])
{
//假设控制点1的t1=0.25
//假设控制点2的t2=0.5
InvalidateRect(NULL);//强制清屏
UpdateWindow();
CDC* pDC = GetDC();
CPen newPen, * oldPen;
newPen.CreatePen(PS_SOLID, 2, RGB(0, 0, 0));
oldPen = pDC->SelectObject(&newPen);
pDC->Polyline(p, 4);
pDC->SelectObject(oldPen);
POINT controlpoint[4];
controlpoint[0] = p[0];//控制点0即为P0
controlpoint[3] = p[3];//控制点1即为P1
controlpoint[1].x = 3.5549 * (p[1].x - 0.4219 * p[0].x - 0.0156 * p[3].x) - 1.3329 * (p[2].x - 0.125 * p[0].x - 0.125 * p[3].x);
controlpoint[1].y = 3.5549 * (p[1].y - 0.4219 * p[0].y - 0.0156 * p[3].y) - 1.3329 * (p[2].y - 0.125 * p[0].y - 0.125 * p[3].y);//反推控制点1坐标
controlpoint[2].x = -3.5549*(p[1].x - 0.4219 * p[0].x - 0.0156 * p[3].x) + 3.9995 * (p[2].x - 0.125 * p[0].x - 0.125 * p[3].x);
controlpoint[2].y = -3.5549 * (p[1].y - 0.4219 * p[0].y - 0.0156 * p[3].y) + 3.9995 * (p[2].y - 0.125 * p[0].y - 0.125 * p[3].y);//反推控制点2坐标
CPen newPen1;
newPen1.CreatePen(PS_SOLID, 2, RGB(0, 0, 255));
oldPen = pDC->SelectObject(&newPen1);
pDC->Polyline(controlpoint, 4);
pDC->MoveTo(p[0].x, p[0].y);
pDC->SelectObject(oldPen);
CPen newPen2;
newPen2.CreatePen(PS_SOLID, 2, RGB(255, 0, 0));
oldPen = pDC->SelectObject(&newPen2);
//反推ax、bx、cx、dx、ay、by、cy、dy
double ax = 8.0 / 3.0 * p[3].x - 16 * p[2].x + 64.0 / 3.0 * p[1].x - 8 * p[0].x;
double ay = 8.0 / 3.0 * p[3].y - 16 * p[2].y + 64.0 / 3.0 * p[1].y - 8 * p[0].y;
double bx = -2 * p[3].x + 20 * p[2].x - 32 * p[1].x + 14 * p[0].x;
double by = -2 * p[3].y + 20 * p[2].y - 32 * p[1].y + 14 * p[0].y;
double cx = -7 * p[0].x + 32.0 / 3.0 * p[1].x - 4 * p[2].x + 1.0 / 3.0 * p[3].x;
double cy = -7 * p[0].y + 32.0 / 3.0 * p[1].y - 4 * p[2].y + 1.0 / 3.0 * p[3].y;
double dx = p[0].x;
double dy = p[0].y;
for (double t = 0; t <= 1; t = t + 0.001) {
int xt = ax * t * t * t + bx * t * t + cx * t + dx;
int yt = ay * t * t * t + by * t * t + cy * t + dy;
pDC->LineTo(xt, yt);
// Sleep(10);
}
pDC->SelectObject(oldPen);
}
5.3 B样条曲线
//以已知的六个点为控制点来绘制B样条曲线
//p:已知的六个控制点
void CDiamondView::DrawBCurve(POINT p[6])
{
InvalidateRect(NULL);//强制清屏
UpdateWindow();
CDC* pDC = GetDC();
CPen newPen, * oldPen;
newPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 0));
oldPen = pDC->SelectObject(&newPen);
pDC->Polyline(p, 6);
pDC->SelectObject(oldPen);
CPen newPen2;
newPen2.CreatePen(PS_SOLID, 3, RGB(255, 0, 0));
oldPen = pDC->SelectObject(&newPen2);
for (int i = 0; i < 3; i++) {
double ax = -(p[i].x - 3 * p[i + 1].x + 3 * p[i + 2].x - p[i + 3].x) / 6;
double ay = -(p[i].y - 3 * p[i + 1].y + 3 * p[i + 2].y - p[i + 3].y) / 6;
double bx = (p[i].x - 2 * p[i + 1].x + p[i + 2].x) / 2;
double by = (p[i].y - 2 * p[i + 1].y + p[i + 2].y) / 2;
double cx = -(p[i].x - p[i + 2].x) / 2;
double cy = -(p[i].y - p[i + 2].y) / 2;
double dx = (p[i].x + 4 * p[i + 1].x + p[i + 2].x) / 6;
double dy = (p[i].y + 4 * p[i + 1].y + p[i + 2].y) / 6;
// pDC->MoveTo(p[i].x, p[i].y);
for (double t = 0; t <= 1; t = t + 0.001) {
int xt = ax * t * t * t + bx * t * t + cx * t + dx;
int yt = ay * t * t * t + by * t * t + cy * t + dy;
pDC->MoveTo(xt, yt);
pDC->LineTo(xt, yt);
// Sleep(10);
}
}
pDC->SelectObject(oldPen);
}
6.程序运行结果

正确地根据4个控制点绘制出了一条Bezier曲线,且将4个控制点连接绘制出来。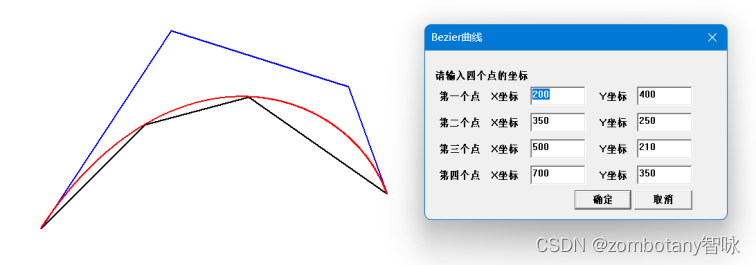
正确地根据曲线上4个点绘制出了一条Bezier曲线能够穿过这4个点,且将这4个点连接绘制出来。并且能够根据曲线本身反推控制点,将这4个点用蓝色的线连接绘制出来。
正确地根据6个控制点绘制了B样条曲线。
7.总结

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)