目录

• 树结构核心概念速览
• 9 大经典树型结构深度剖析
• 树结构应用场景与避坑指南
• 高频面试题实战解析
• 总结与学习资源推荐

前言

在数据结构的世界里，树型结构凭借其独特的层级关系和高效的数据处理能力，成为程序员必须掌握的核心知识。无论是算法面试、日常开发，还是系统架构设计，树结构的身影无处不在。本文将带你深入拆解 9 种经典树型结构，用最通俗的语言、最实用的案例，帮你彻底吃透这些高频考点！

一、树结构核心概念速览

树结构以分层的方式组织数据，每个节点可以有零个或多个子节点。理解树结构，需掌握几个核心术语：

• 根节点：树的顶层节点，没有父节点
• 子节点：被其他节点直接连接的节点
• 叶子节点：没有子节点的节点
• 树的高度：从根节点到最远叶子节点的最长路径上的节点数

不同类型的树通过特定的约束条件，实现不同的功能需求。接下来我们逐一拆解！

二、9 大经典树型结构深度剖析

1. 完全二叉树

定义：除最后一层外，其余层节点数全满，且最后一层节点从左到右连续排列。
核心特点：

• 可使用数组高效存储（节点 i 的左子节点为 2i+1，右子节点为 2i+2）
• 层序遍历判断：若遇到空节点后仍有非空节点，则不是完全二叉树
  应用场景：优先队列、堆排序的底层实现

      A
    /   \
   B     C
  / \   / 
 D  E  F   

2. 满二叉树

定义：所有层节点数均达到最大值，节点总数为 2^h - 1（h 为树高）。
硬核公式：

节点总数 = 2^高度 - 1

记忆技巧：每层节点数呈 2^0, 2^1, 2^2... 指数增长

      A
    /   \
   B     C
  / \   / \
 D   E F   G

3. 二叉搜索树（BST）

核心规则：

• 左子树所有节点值 < 根节点值
• 右子树所有节点值 > 根节点值
• 左右子树均为 BST
  致命缺陷：极端情况下会退化为链表，导致查找效率从 O(log n) 暴跌至 O(n)！
  性能优化：引入平衡机制（如 AVL 树、红黑树）

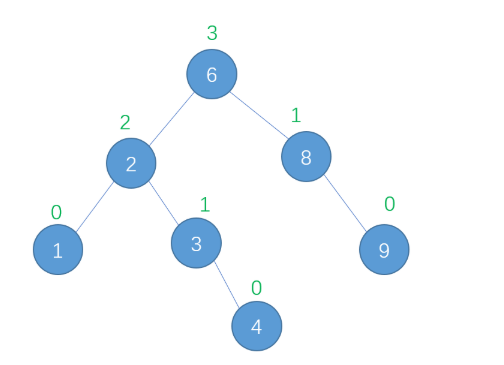
      5
    /   \
   3     7
  / \   / \
 2   4 6   8

4. 平衡二叉树（AVL 树 & 红黑树）

AVL 树：

• 严格要求左右子树高度差不超过 1
• 通过左旋、右旋操作保持平衡
• 适用场景：对查询性能要求极高的场景（如数据库索引）

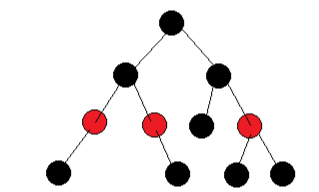
红黑树：

• 通过颜色标记（红 / 黑）实现近似平衡
• 规则：
  1. 根节点和叶子节点为黑色
  2. 红色节点的子节点必须为黑色
  3. 任意路径的黑节点数量相同
• 经典应用：Java 的 TreeMap、C++ 的 std::map

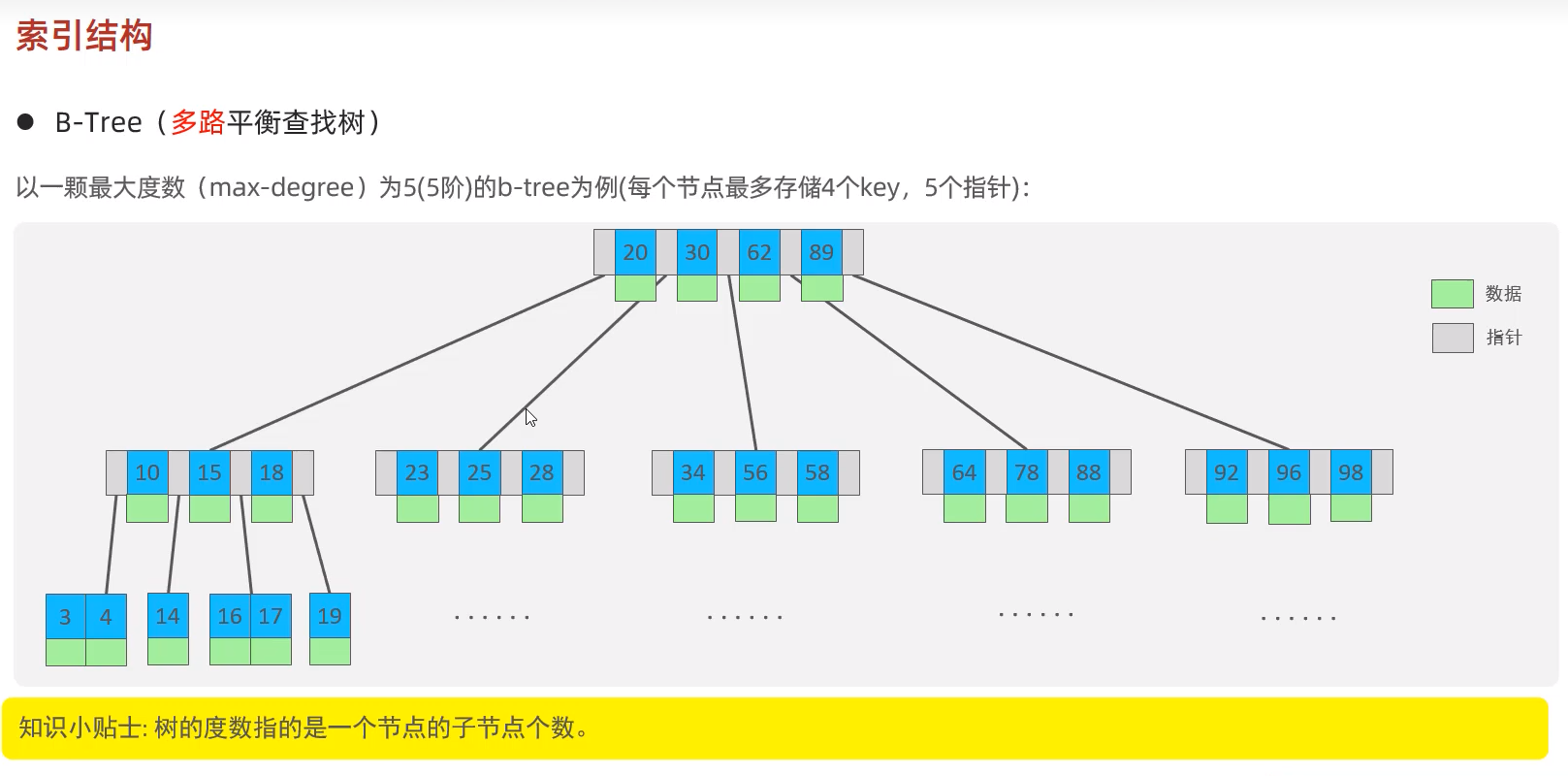
5. B 树 & B + 树

很相似，所以放一起对比。

B 树：

• 多路平衡搜索树，每个节点可存多个键值对
• 核心优势：减少磁盘 I/O 次数，适合外存数据存储

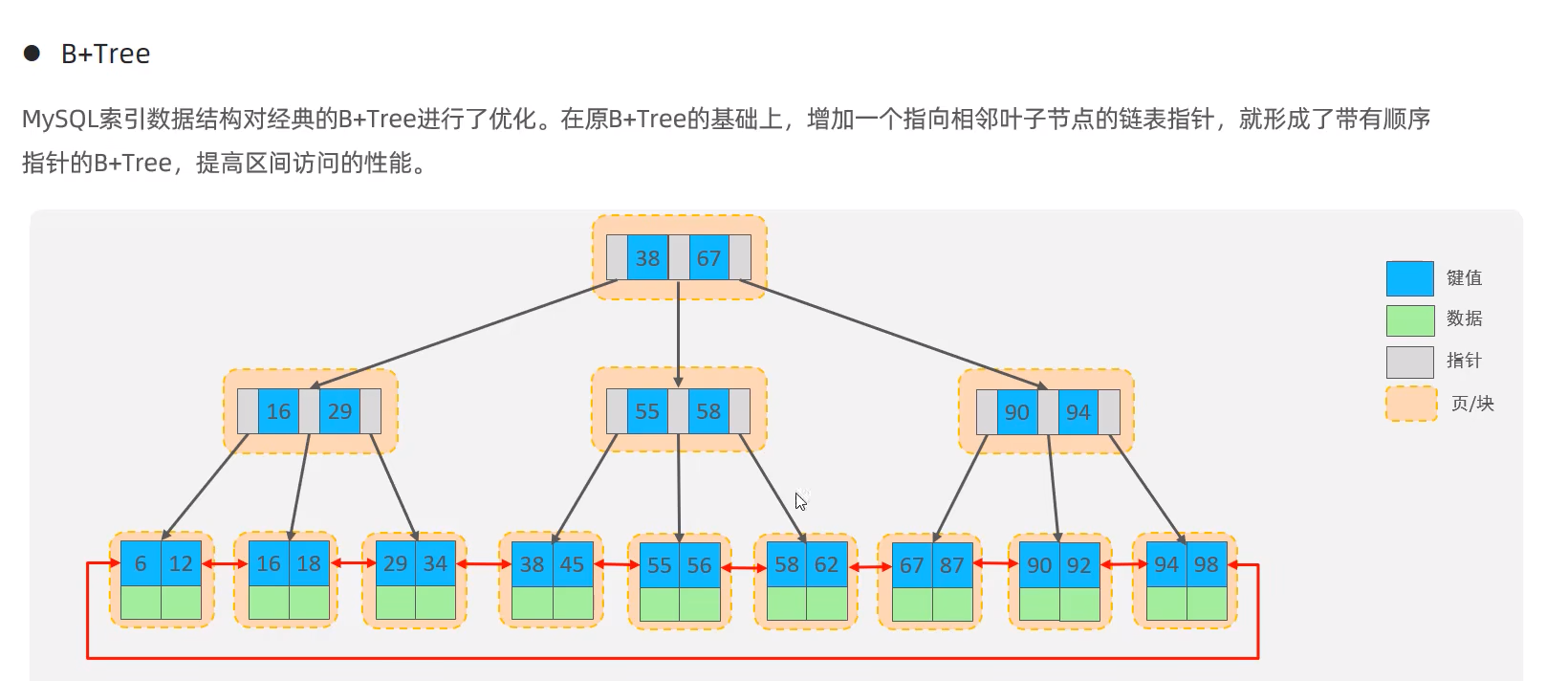
B + 树（数据库索引神器！）：

详情可看：一文通俗讲解MySQL数据库常见面试题-CSDN博客

• 非叶子节点仅存键，数据全在叶子节点
• 叶子节点用链表串联，支持高效范围查询
• 场景：MySQL、MongoDB 等数据库的索引结构

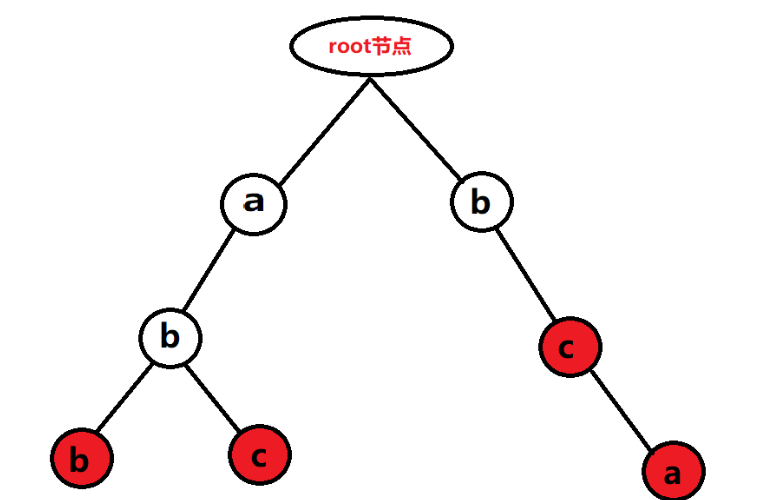
6. 字典树（前缀树）

逆天功能：字符串集合的高效存储与检索，通过共享前缀大幅节省空间！
经典案例：

• 搜索引擎自动补全
• 拼写检查
• IP 路由最长前缀匹配

结构特点：根节点为空，从根到叶子的路径构成完整字符串

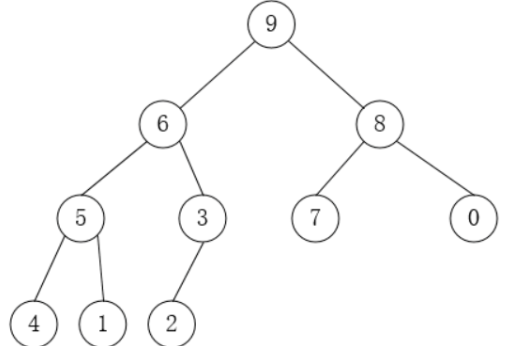
7. 堆（最大堆 & 最小堆）

核心性质：

• 最大堆：父节点值 ≥ 子节点值
• 最小堆：父节点值 ≤ 子节点值

必知应用：

• 优先队列（Java 的 PriorityQueue 底层实现）
• 堆排序（时间复杂度 O(n log n)）
• Top K 问题求解

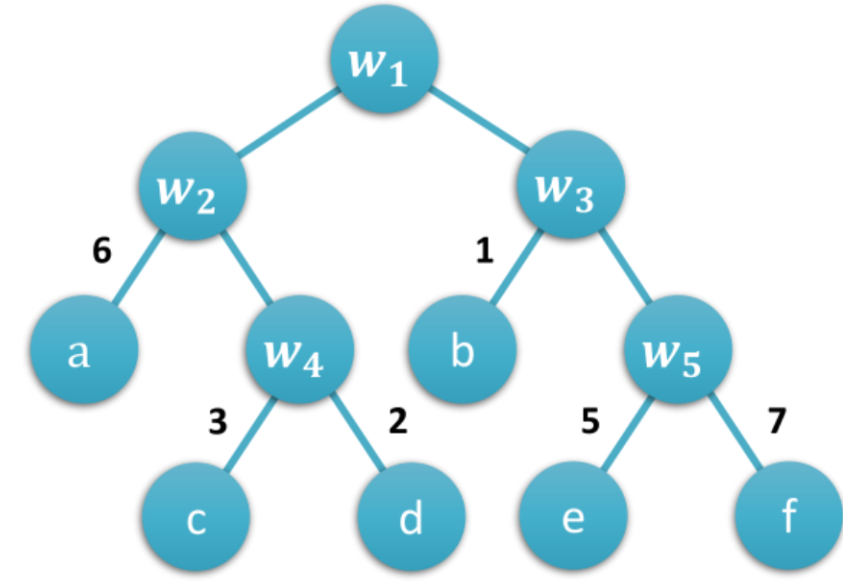
8. 哈夫曼树

终极目标：构建带权路径长度最短的二叉树，实现数据压缩！
构建三步法：

1. 将每个字符视为单节点树，权重设为出现频率
2. 合并权重最小的两棵树，生成新树（权重为两者之和）
3. 重复步骤 2，直至只剩一棵树

实战场景：

• ZIP 文件压缩
• 通信编码（减少数据传输量）

三、树结构应用场景与避坑指南

结构类型	典型应用场景	常见陷阱
二叉搜索树	快速查找（但需防退化！）	未平衡化时性能暴跌
红黑树	Map/Set 集合底层实现	插入删除时需维护颜色规则
B + 树	数据库索引	理解非叶子节点与叶子节点的分工
字典树	字符串检索	内存占用需谨慎评估

四、高频面试题实战解析

面试题 1：如何判断一棵二叉树是否为平衡二叉树？
解题思路：后序遍历 + 高度判断，递归计算左右子树高度差

面试题 2：为什么 MySQL 索引使用 B + 树而不是 B 树？
关键回答：

1. B + 树所有数据在叶子节点，查询效率更稳定
2. 叶子节点链表结构支持范围查询
3. 减少磁盘 I/O 次数，提升查询性能

五、总结与学习资源推荐

树型结构看似复杂，但只要抓住每种结构的核心约束与应用场景，就能轻松驾驭！建议通过 LeetCode 专项训练（如二叉树、堆相关题目）巩固知识。

精华速记：

• 平衡树保效率：AVL 树严格平衡，红黑树近似平衡
• B + 树赢在磁盘：数据库索引的不二之选
• 字典树省空间：字符串处理的秘密武器