本文未经允许禁止转载
B站：https://space.bilibili.com/455965619
作者：Heskey0 / 赫斯基皇

一.布置场景

场景中总共有9个物体

• 6个 plane
• 1个 box
• 1个 sphere
• 1个 light

我将在此章节介绍这些物体相关的计算

注意：我们首先计算光线命中这些物体的点和光源到命中点的距离

1.plane

要表示一个plane，可以通过 点法式，所以我们总共需要两个数据

position : plane的位置
normal : plane的法向量

(1)我们首先计算光线与plane是否相交，并且求出此交点
在此之前，我们还需要传入另外两个表示光线的数据

position : 光源的位置
direction : 光的方向

注：d和norm均为 单位向量

def intersect_plane(pos, d, p, norm):
    dist = inf
    hit_pos = ti.Vector([0.0, 0.0, 0.0])
    denom = d.dot(norm)
    if abs(denom) > 0.0001:    # 光与平面不平行
        dist = norm.dot(p - pos) / denom
        hit_pos = pos + d * dist
    return dist, hit_pos

在这段代码中，我们传入参数 light_position, light_direction, plane_position, plane_normal，然后返回 命中点到光源的距离，命中点坐标
由于d和norm为单位向量，所以denom即d和norm夹角的cosine值，如果denom的绝对值 = 0，那么光线与平面不相交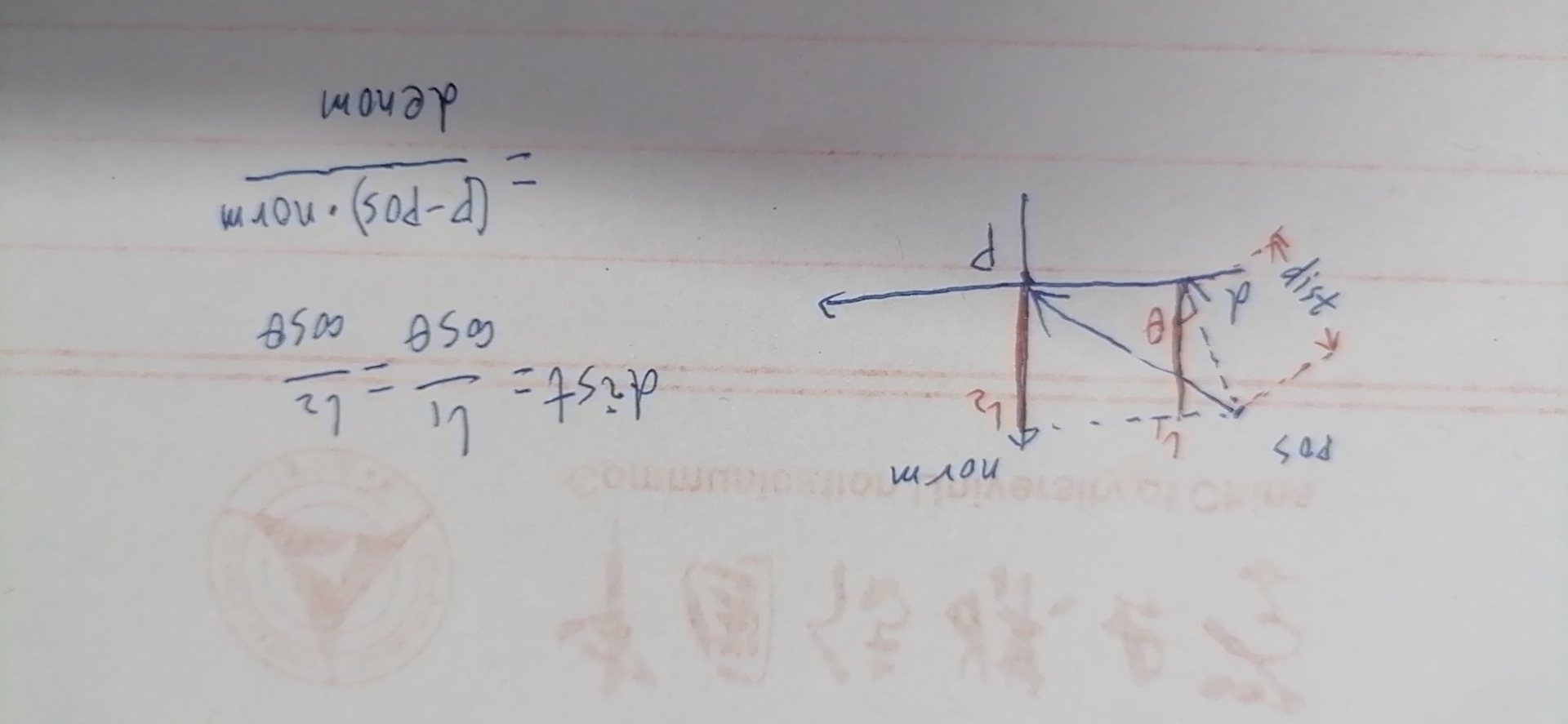

由l1=l2，denom=cos(θ)求出dist，最后根据dist求出hit_pos

2.sphere

要表示一个空间中的球，我们总共需要两个数据

position : 球的坐标
radius : 球的半径

代码如下：传入数据为pos:light_position 和 d:light_dir

def intersect_sphere(pos, d, center, radius):   
    # 构建余弦定理三角形:判断光与球是否相交
    T = pos - center
    A = 1.0	
    B = 2.0 * T.dot(d)
    C = T.dot(T) - radius * radius
    delta = B * B - 4.0 * A * C
    dist = inf
    hit_pos = ti.Vector([0.0, 0.0, 0.0])

    if delta > 0:       # 有解
        delta = ti.max(delta, 0)
        sdelta = ti.sqrt(delta)
        ratio = 0.5 / A
        ret1 = ratio * (-B - sdelta)    # 方程的解, 即三角形的边长(离入射光近的点)
        dist = ret1
        hit_pos = pos + d * dist

    return dist, hit_pos

在这段代码中，我们构建了一个三角形，它的三条边为

1. 光源 与 球心 的连线
2. 光源 与 命中点 的连线
3. 命中点 与 球心 的连线

对第3条边使用余弦定理得到一个方程组
代码中A,B,C为二元一次方程Ax^2 + Bx + C = 0的系数，用二元一次方程的求根公式可求出第2条边的长度，即dist，最后根据dist求出hit_pos

3.box

要表示一个box，我们需要的不仅仅是坐标数据，因为 box的旋转与缩放不可忽略 ，所以我们首先介绍box的矩阵变换

注：对矩阵原理不熟悉的读者可先学习 《计算机图形学》 ，这里不做赘述
（1）点的变换

def point(m, p):
    hp = ti.Vector([p[0], p[1], p[2], 1.0])
    hp = m @ hp
    hp /= hp[3]
    return ti.Vector([hp[0], hp[1], hp[2]])

(2) 向量的变换

def vec(m, v):
    hv = ti.Vector([v[0], v[1], v[2], 0.0])
    hv = m @ hv
    return ti.Vector([hv[0], hv[1], hv[2]])

(3) 光线与box的相交计算

def intersect(box_min, box_max, o, d):     # box_min, box_max, pos(box空间), ray_dir(box空间)
    intersect = 1   # 光与box是否相交

    near_t = -inf
    far_t = inf
    near_face = 0
    near_is_max = 0

    for i in ti.static(range(3)):       # ti.static(range()) can iterate matrix elements
        if d[i] == 0:   # 光平行于包围体的一个面
            if o[i] < box_min[i] or o[i] > box_max[i]:
                intersect = 0
        else:
            i1 = (box_min[i] - o[i]) / d[i]     # 处理该维度的坐标
            i2 = (box_max[i] - o[i]) / d[i]

            new_far_t = max(i1, i2)     # box检测时, 为i2
            new_near_t = min(i1, i2)    # box检测时, 为i1
            new_near_is_max = i2 < i1   # box检测时, 为true

            far_t = min(new_far_t, far_t)   # box检测时, 为i2三个维中最小的值
            if new_near_t > near_t:         # near_t    为i1三个维中最大的值
                near_t = new_near_t
                near_face = int(i)          # 记录最小的i所在的维
                near_is_max = new_near_is_max   # 在当前维中near_t, i2<i1 ?

    near_norm = ti.Vector([0.0, 0.0, 0.0])
    if near_t > far_t:
        intersect = 0
    if intersect:
        for i in ti.static(range(2)):
            if near_face == i:
                near_norm[i] = -1 + near_is_max * 2
    return intersect, near_t, far_t, near_norm      # 是否相交,

# box
def intersect_transformed(box_min, box_max, o, d):
    # 射线转换到包围体的local position
    obj_o = mat_mul_point(box_m_inv, o)
    obj_d = mat_mul_vec(box_m_inv, d)
    intersect, near_t, _, near_norm = intersect(box_min, box_max, obj_o, obj_d)

    if intersect and 0 < near_t:
        near_norm = mat_mul_vec(box_m_inv_t, near_norm)
    else:
        intersect = 0
    return intersect, near_t, near_norm

对代码的解释都写在注释里面了，还请大家耐心阅读

4.light

在此文中使用的light是方形的，light其实就是一个box，我们只需要复用上面的代码即可

def intersect_light(pos, ray_dir, tmax):
    hit, t, far_t, near_norm = intersect_aabb(light_min_pos, light_max_pos, pos, ray_dir)
    if hit and 0 < t < tmax:
        hit = 1
    else:
        hit = 0
        t = inf
    return hit, t