正向运动学和反向运动学

目录

1. 2D中的旋转矩阵
2. sympy包
3. 旋转的合成
4. 旋转矩阵中的欧拉角
5. 平移
6. 齐次变换及其逆变换
7. 齐次变换的合成
8. Denavit-Hartenberg 参数
9. DH参数分配算法
10. 正向运动学
11. 反向运动学
12. 反向运动学举例

1.2D中的旋转矩阵

在正向运动学之前，我们需要知道如何在不同的坐标系中表示向量。这时候就需要用到旋转矩阵的定义了。

旋转矩阵有两个概念上但数学上等价的解释。它们可以被看作是用其他坐标系表示一个坐标系中的向量的一种方法。这种解释被称为坐标系之间的“映射”。

或者，旋转矩阵可以看作是一个“算子”，它实际上在一个坐标系中移动一个向量。注意这种概念上的区别是很重要的，因为特定的应用程序将规定使用哪个描述。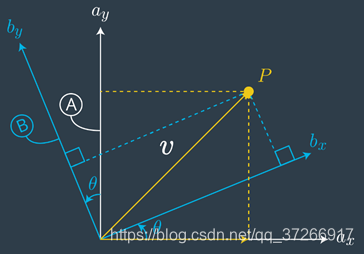

现在有一个向量v，它在A坐标系中的测量坐标我们已经知道了，现在要将它在B坐标系中表示出来。

$\mathbf{v}={\mathbf{v}}_{\mathbf{x}}{\hat{\mathbf{a}}}_{\mathbf{x}}+{\mathbf{v}}_{\mathbf{y}}{\hat{\mathbf{a}}}_{\mathbf{y}}={\mathbf{u}}_{\mathbf{x}}{\hat{\mathbf{b}}}_{\mathbf{x}}+{\mathbf{u}}_{\mathbf{x}}{\hat{\mathbf{b}}}_{\mathbf{x}}$
(1)

公式（1）点乘 ${\hat{\mathbf{a}}}_{\mathbf{x}}$得到

$\mathbf{v}.{\hat{\mathbf{a}}}_{\mathbf{x}}={\mathbf{v}}_{\mathbf{x}}{\hat{\mathbf{a}}}_{\mathbf{x}}.{\hat{\mathbf{a}}}_{\mathbf{x}}+{\mathbf{v}}_{\mathbf{y}}{\hat{\mathbf{a}}}_{\mathbf{x}}.{\hat{\mathbf{a}}}_{\mathbf{y}}={\mathbf{u}}_{\mathbf{x}}{\hat{\mathbf{a}}}_{\mathbf{x}}.{\hat{\mathbf{b}}}_{\mathbf{x}}+{\mathbf{u}}_{\mathbf{y}}{\hat{\mathbf{a}}}_{\mathbf{x}}.{\hat{\mathbf{b}}}_{\mathbf{y}}$
(2)

因为 ${\hat{\mathbf{a}}}_{\mathbf{x}}$和 ${\hat{\mathbf{a}}}_{\mathbf{y}}$ 是正交单位向量，所以 ${\hat{\mathbf{a}}}_{\mathbf{x}}\cdot {\hat{\mathbf{a}}}_{\mathbf{x}}=1$
且 ${\hat{\mathbf{a}}}_{\mathbf{x}}\cdot {\hat{\mathbf{a}}}_{\mathbf{y}}=0$所以公式（2）可以化简成：

${\mathbf{v}}_{\mathbf{x}}={\mathbf{u}}_{\mathbf{x}}{\hat{\mathbf{a}}}_{\mathbf{x}}.{\hat{\mathbf{b}}}_{\mathbf{x}}+{\mathbf{u}}_{\mathbf{y}}{\hat{\mathbf{a}}}_{\mathbf{x}}.{\hat{\mathbf{b}}}_{\mathbf{y}}$
(3)

类似的，我们使用 ${\hat{\mathbf{a}}}_{\mathbf{y}}$点乘（1）然后化简，我们就得到了

${\mathbf{v}}_{\mathbf{y}}={\mathbf{u}}_{\mathbf{x}}{\hat{\mathbf{a}}}_{\mathbf{y}}.{\hat{\mathbf{b}}}_{\mathbf{x}}+{\mathbf{u}}_{\mathbf{y}}{\hat{\mathbf{a}}}_{\mathbf{y}}.{\hat{\mathbf{b}}}_{\mathbf{y}}$
(4)

我们可以把方程(3)和(4)整理成更紧凑的矩阵形式，

$\left[\begin{array}{c}{v}_x\\ v_y\end{array}\right]=\left[\begin{array}{cc}{\hat{a}}_x.{\hat{b}}_x& {\hat{a}}_x.{\hat{b}}_y\\ {\hat{a}}_y.{\hat{b}}_x& {\hat{a}}_y.{\hat{b}}_y\end{array}\right]\left[\begin{array}{c}{u}_x\\ u_y\end{array}\right]$
(5)

化简得：
$\left[\begin{array}{c}{v}_x\\ v_y\end{array}\right]=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\left[\begin{array}{c}{u}_x\\ u_y\end{array}\right]$
(6)

等式(5)右边的第一项称为旋转矩阵，通常写成更紧凑的形式${}_b^{a}R$ 。
它们实际上是坐标系B的基向量用坐标系A表示，也就是说，

${}_{\mathbf{B}}^{\mathbf{A}}\text{R}=\left[\begin{array}{cc}{}^A{\hat{b}}_x& {}^A{\hat{b}}_y\end{array}\right]=\left[\begin{array}{cc}{\hat{a}}_x.{\hat{b}}_x& {\hat{a}}_x.{\hat{b}}_y\\ {\hat{a}}_y.{\hat{b}}_x& {\hat{a}}_y.{\hat{b}}_y\end{array}\right]=\left[\begin{array}{c}{}^B{\hat{a}}_x{}^T\\ {}^B{\hat{a}}_y{}^T\end{array}\right]$

从A到B的旋转等于从B到A旋转的转置.事实上,因为旋转矩阵是正交矩阵(由正交单位向量),它有几个属性,总结如下，证明省略。
旋转矩阵的重要性质${}_B^{A}R$：

1. 转置等于它的逆矩阵。
2. 行列式等于+1(假设是一个右手坐标系)
3. 列(和行)是互相正交的单位向量，因此，任意列(或行)的大小等于1，任意两列(或行)的点积等于零
4. 列定义基向量(即x, y, z轴)相对于基坐标系旋转后的坐标系

增加更多维度

到目前为止，我们只考虑了二维旋转，但相同的属性适用于三维旋转.

${}_B^A\text{R}=\left[\begin{array}{ccc}{}^A{\hat{b}}_x& {}^A{\hat{b}}_y& {}^A{\hat{b}}_z\end{array}\right]=\left[\begin{array}{ccc}{\hat{a}}_x.{\hat{b}}_x& {\hat{a}}_x.{\hat{b}}_y& {\hat{a}}_x.{\hat{b}}_z\\ {\hat{a}}_y.{\hat{b}}_x& {\hat{a}}_y.{\hat{b}}_y& {\hat{a}}_y.{\hat{b}}_z\\ {\hat{a}}_z.{\hat{b}}_x& {\hat{a}}_z.{\hat{b}}_y& {\hat{a}}_z.{\hat{b}}_z\end{array}\right]$

2.sympy包

SymPy是一个功能齐全的计算机代数系统（CAS），它能够以符号方式构造和操作矩阵，然后在需要时对其进行数值计算。

从符号上推导表达式有两个优点。首先，看到这些方程可以让你对系统有更多的了解，至少对于相对简单的系统是这样。其次，还有数量上的优势。由于计算机不能无限精确地执行浮点运算，因此浮点运算本身就存在一定的误差，而且误差会随着运算次数的增加而增加。

需要从SymPy和NumPy导入一些函数。

from sympy import symbols, cos, sin, pi, simplify
from sympy.matrices import Matrix
import numpy as np

接下来，定义将在旋转矩阵中使用的符号。

### 为常用“q”表示的联合变量创建符号
### 联合变量“q”等于“ϴ”或“d”决定于关节的转动或平移
q1, q2, q3, q4 = symbols('q1:5') 
# 不相关的符号可以这样定义:
A, R, O, C = symbols('A R O C')

对于旋转，大多数函数都期望角度作为弧度输入;然而，大多数人认为度的单位更直观。定义可重用转换因子通常是一个好主意。

# 转换因子
rtd = 180./np.pi # 弧度转角度
dtr = np.pi/180. # 角度转弧度

现在我们分别为X，Y和Z轴创建基本旋转的旋转矩阵。使用Matrix对象构造矩阵。

R_x = Matrix([[ 1,              0,        0],
              [ 0,        cos(q1), -sin(q1)],
              [ 0,        sin(q1),  cos(q1)]])

R_y = Matrix([[ cos(q2),        0,  sin(q2)],
              [       0,        1,        0],
              [-sin(q2),        0,  cos(q2)]])

R_z = Matrix([[ cos(q3), -sin(q3),        0],
              [ sin(q3),  cos(q3),        0],
              [ 0,              0,        1]])

最后，让我们用数字方法评估矩阵。这里发生的是将字典传递给符号表达式，并且该evalf方法将其作为浮点进行计算。字典允许同时替换多个值。

print("Rotation about the X-axis by 45-degrees")
print(R_x.evalf(subs={q1: 45*dtr}))
print("Rotation about the y-axis by 45-degrees")
print(R_y.evalf(subs={q2: 45*dtr}))
print("Rotation about the Z-axis by 30-degrees")
print(R_z.evalf(subs={q3: 30*dtr}))

输出如下：

Rotation about the X-axis by 45-degrees
Matrix([[1.00000000000000, 0, 0], [0, 0.707106781186548, -0.707106781186547], [0, 0.707106781186547, 0.707106781186548]])
Rotation about the y-axis by 45-degrees
Matrix([[0.707106781186548, 0, 0.707106781186547], [0, 1.00000000000000, 0], [-0.707106781186547, 0, 0.707106781186548]])
Rotation about the Z-axis by 30-degrees
Matrix([[0.866025403784439, -0.500000000000000, 0], [0.500000000000000, 0.866025403784439, 0], [0, 0, 1.00000000000000]])

3.旋转的合成

尽管欧拉角和旋转矩阵相对直观，但它们确实存在两个明显的缺点。

首先是与数值表现有关的问题。在三维环境中定义刚体的方向只需要三个广义坐标；但是旋转矩阵包含九个元素。显然，并非所有九个元素都是独立的，并且捕获方向信息所需的内存比使用的最小集合所需的更多。

旋转矩阵在数值上也不是很稳定。与旋转矩阵的重复乘法相关的舍入误差也会造成数值漂移。这意味着随着时间的推移，正交性条件会被破坏，矩阵将不再是一个有效的旋转矩阵。此外，在两个旋转矩阵之间平滑地插值是一项非常重要的任务.

第二个显著的缺点是表示的奇点(不要与运动学奇点混淆)。当序列中的第二次旋转使得第一坐标系和第三坐标系对齐，导致自由度损失时，表示的奇点就会出现。这种情况通常称为“万向节死锁（gimbal lock）”。在方程（4）中使用的ZYX旋转序列的情况下,当$\beta =\pi /2$观察整体旋转矩阵发生了什么。

${}_{\mathbf{B}}^{\mathbf{A}}{\text{R}}_{\mathbf{Z}\mathbf{Y}\mathbf{X}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& c_{\gamma }& -s_{\gamma }\\ 0& s_{\gamma }& c_{\gamma }\end{array}\right]\left[\begin{array}{ccc}{c}_{\pi /2}& 0& s_{\pi /2}\\ 0& 1& 0\\ -s_{\pi /2}& 0& c_{\pi /2}\end{array}\right]\left[\begin{array}{ccc}{c}_{\alpha }& -s_{\alpha }& 0\\ s_{\alpha }& c_{\alpha }& 0\\ 0& 0& 1\end{array}\right]$

${}_{\mathbf{B}}^{\mathbf{A}}{\text{R}}_{\mathbf{Z}\mathbf{Y}\mathbf{X}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& c_{\gamma }& -s_{\gamma }\\ 0& s_{\gamma }& c_{\gamma }\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ -1& 0& 0\end{array}\right]\left[\begin{array}{ccc}{c}_{\alpha }& -s_{\alpha }& 0\\ s_{\alpha }& c_{\alpha }& 0\\ 0& 0& 0\end{array}\right]$

${}_{\mathbf{B}}^{\mathbf{A}}{\text{R}}_{\mathbf{Z}\mathbf{Y}\mathbf{X}}=\left[\begin{array}{ccc}0& 0& 1\\ s_{\gamma }& c_{\gamma }& 0\\ -c_{\gamma }& s_{\gamma }& 0\end{array}\right]\left[\begin{array}{ccc}{c}_{\alpha }& -s_{\alpha }& 0\\ s_{\alpha }& c_{\alpha }& 0\\ 0& 0& 1\end{array}\right]$

${}_{\mathbf{B}}^{\mathbf{A}}{\text{R}}_{\mathbf{Z}\mathbf{Y}\mathbf{X}}=\left[\begin{array}{ccc}0& 0& 1\\ s_{\alpha +\gamma }& s_{\alpha +\gamma }& 0\\ -c_{\alpha +\gamma }& s_{\alpha +\gamma }& 0\end{array}\right]$

可以参考此处关于万向节死锁的解释。

可以看到，无论 $\alpha$ 和 $\gamma$角度是多少，它们对X分量都没有影响。值得注意的是，没有什么错误或物理上抑制旋转运动，这是一个数学上的缺陷，在欧拉坐标系中。此外，所有只用三个参数描述方向的约定都存在表示的奇异性。因此，在实际中使用欧拉角的一个关键考虑是确保运动范围不接近奇点。

下面是一个是矩阵关于Y轴和Z轴旋转的程序：

from sympy import symbols, cos, sin, pi, sqrt
from sympy.matrices import Matrix

# 为联合变量创建符号
q1, q2 = symbols('q1:3')

# 创建一个表示旋转固有序列的符号矩阵关于Y轴和Z轴。
# 让绕Y轴的旋转用q1表示，绕Z轴的旋转用q2表示。

####### TO DO ########
# 用适当的(符号)初等旋转矩阵替换R_y和R_z，然后计算YZ_intrinsic。
R_y = Matrix([[ cos(q1),        0, sin(q1)],
              [ 0,              1,       0],
              [-sin(q1),        0, cos(q1)]])
R_z = Matrix([[ cos(q2), -sin(q2),       0],
              [ sin(q2),  cos(q2),       0],
              [       0,        0,       1]])

YZ_intrinsic_sym = R_y * R_z
YZ_intrinsic_num = YZ_intrinsic_sym.evalf(subs={q1: pi/4, q2: pi/3})

4.旋转矩阵中的欧拉角

在许多情况下，特别是涉及反向运动学的情况下，我们得到一个复合旋转矩阵，有必要找到一组欧拉角来产生这种旋转。具体过程解取决于欧拉角的选择，但基本过程是相同的。现在使用一个例子来说明一般的过程。

考虑外在因素(例如:(固定轴)X-Y-Z旋转顺序。复合旋转矩阵为，
${}_{\mathbf{B}}^{\mathbf{A}}{\text{R}}_{\mathbf{X}\mathbf{Y}\mathbf{Z}}={\mathbf{R}}_{\mathbf{Z}}(\alpha ){\mathbf{R}}_{\mathbf{Y}}(\beta ){\mathbf{R}}_{\mathbf{X}}(\gamma )$
${}_{\mathbf{B}}^{\mathbf{A}}{\text{R}}_{\mathbf{X}\mathbf{Y}\mathbf{Z}}=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]=\left[\begin{array}{ccc}{c}_{\alpha }{c}_{\beta }& c_{\alpha }{s}_{\beta }{s}_{\gamma }-s_{\alpha }{c}_{\gamma }& c_{\alpha }{s}_{\beta }{c}_{\gamma }+s_{\alpha }{s}_{\gamma }\\ s_{\alpha }{c}_{\beta }& s_{\alpha }{s}_{\beta }{s}_{\gamma }+c_{\alpha }{c}_{\gamma }& s_{\alpha }{s}_{\beta }{c}_{\gamma }-c_{\alpha }{s}_{\gamma }\\ -s_{\beta }& c_{\beta }{s}_{\gamma }& c_{\beta }{c}_{\gamma }\end{array}\right]$
目标是找到角度$\alpha$，$\beta$和$\gamma$，给定数值 $r_{ij}$.解决方案是使用$r_{ij}$的各种组合。这样每个角都可以单独单独解出来。使用尽可能简单的术语似乎是一种谨慎的策略，用正弦或余弦函数的倒数来求角度不是一个好主意。原因是符号的模糊性:如果-sin($\beta$) = 0.5，那么角度在哪个象限?使用atan2函数可以避免这种歧义。语法取决于使用的语言或库，但通常是:atan2(y, x)。

关于atan2可以参考这里。

因此，通过识别，可以找到$\beta$

$\beta$: $\beta =\mathbf{a}\mathbf{t}\mathbf{a}\mathbf{n}2(\mathbf{y},\mathbf{x})=\mathbf{a}\mathbf{t}\mathbf{a}\mathbf{n}2(-{\mathbf{r}}_{31},\sqrt{{\mathbf{r}}_{11}\ast {\mathbf{r}}_{11}+{\mathbf{r}}_{21}\ast {\mathbf{r}}_{21}})$

$\gamma$: $\gamma =\mathbf{a}\mathbf{t}\mathbf{a}\mathbf{n}2({\mathbf{r}}_{32},{\mathbf{r}}_{33})$

$\alpha$:$\alpha =\mathbf{a}\mathbf{t}\mathbf{a}\mathbf{n}2({\mathbf{r}}_{21},{\mathbf{r}}_{11})$

注意：当cos($\beta$) = 0时，也就是= +/-90度时，atan2是无定义的，正如我们在欧拉角中看到的，系统表现出奇异的表示形式。

import numpy as np
from sympy.matrices import Matrix
from sympy import symbols, atan2, sqrt

# 转换因子
rtd = 180/np.pi
dtr = np.pi/180

# Fixed Axis X-Y-Z Rotation Matrix
R_XYZ = Matrix([[ 0.353553390593274, -0.306186217847897, 0.883883476483184],
                [ 0.353553390593274,  0.918558653543692, 0.176776695296637],
                [-0.866025403784439,               0.25, 0.433012701892219]])

# 从旋转矩阵中找出需要的项
r31 = R_XYZ[2,0]
r11 = R_XYZ[0,0]
r21 = R_XYZ[1,0]
r32 = R_XYZ[2,1]
r33 = R_XYZ[2,2]


# 旋转矩阵的欧拉角
# sympy 语法 ：  atan2(y, x)
beta  = atan2(-r31, sqrt(r11 * r11 + r21 * r21)) * rtd
gamma = atan2(r32, r33) * rtd
alpha = atan2(r21, r11) * rtd


print("alpha is = ",alpha*dtr, "radians", "or ", alpha, "degrees")
print("beta  is = ",beta*dtr,  "radians", "or ", beta, "degrees")
print("gamma is = ",gamma*dtr, "radians", "or ", gamma, "degrees")

其输出如下：

alpha is =  0.785398163397448 radians or  45.0000000000000 degrees
beta  is =  1.04719755119660 radians or  60.0000000000000 degrees
gamma is =  0.523598775598299 radians or  30.0000000000000 degrees

5.平移

与旋转参照系相比，平移要简单得多。这里我们考虑两个参考系，A和B，它们有相同的方向，但是它们的原点是$A_0$和$B_0$。P点的位置，相对于B坐标系是由${}^B\mathbf{r}P/Bo$向量表示。前导上标表示这个向量在_B坐标系中表示。换句话说,

${}^{\mathbf{B}}{\mathbf{r}}_{\mathbf{P}/{\mathbf{B}}_0}={\mathbf{r}}_{{\mathbf{B}}_{\mathbf{x}}}{\hat{\mathbf{b}}}_{\mathbf{x}}+{\mathbf{r}}_{{\mathbf{B}}_{\mathbf{y}}}{\hat{\mathbf{b}}}_{\mathbf{y}}+{\mathbf{r}}_{{\mathbf{B}}_{\mathbf{z}}}{\hat{\mathbf{b}}}_{\mathbf{z}}$

但目标是描述P相对于$A_0$,${}^A\mathbf{r}P/Bo$

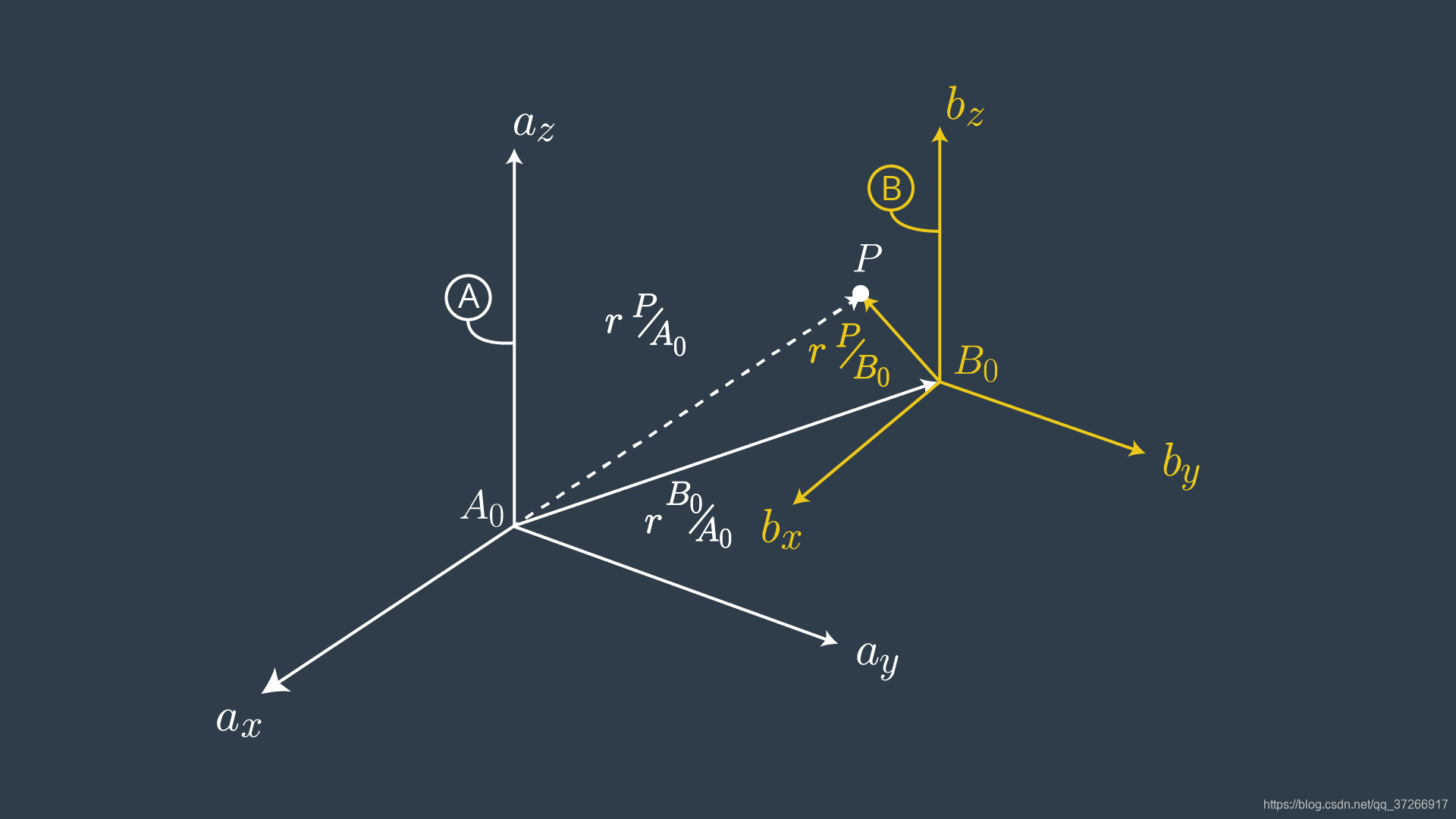因为两个坐标系有相同的相对方向，描述P相对于$A_0$
只需要简单的向量加法:

${}^{\mathbf{A}}{\mathbf{r}}_{\mathbf{P}/{\mathbf{A}}_0}{=}^{\mathbf{A}}{\mathbf{r}}_{{\mathbf{B}}_0/{\mathbf{A}}_0}{+}^{\mathbf{B}}{\mathbf{r}}_{\mathbf{P}/{\mathbf{B}}_0}$

其中${}^{A}rBo/Ao$是_B坐标系相对于A坐标系的原点的原点。值得注意的是，点P的位置并没有发生任何变化，这里只是简单地描述了它相对于另一个参照系的位置。

6.齐次变换及其逆变换

现在考虑一个更一般的情况，两个参照系同时旋转并相互平移。对于点P，它的位置相对于$B_0$是已知的，我们想找到向量${}^A\mathbf{r}P/Bo$。在_A和B坐标系方向相同的情况下，通过向量加法很容易得到解。如果我们知道如何使一帧相对于另一帧旋转，我们就能解决这个问题。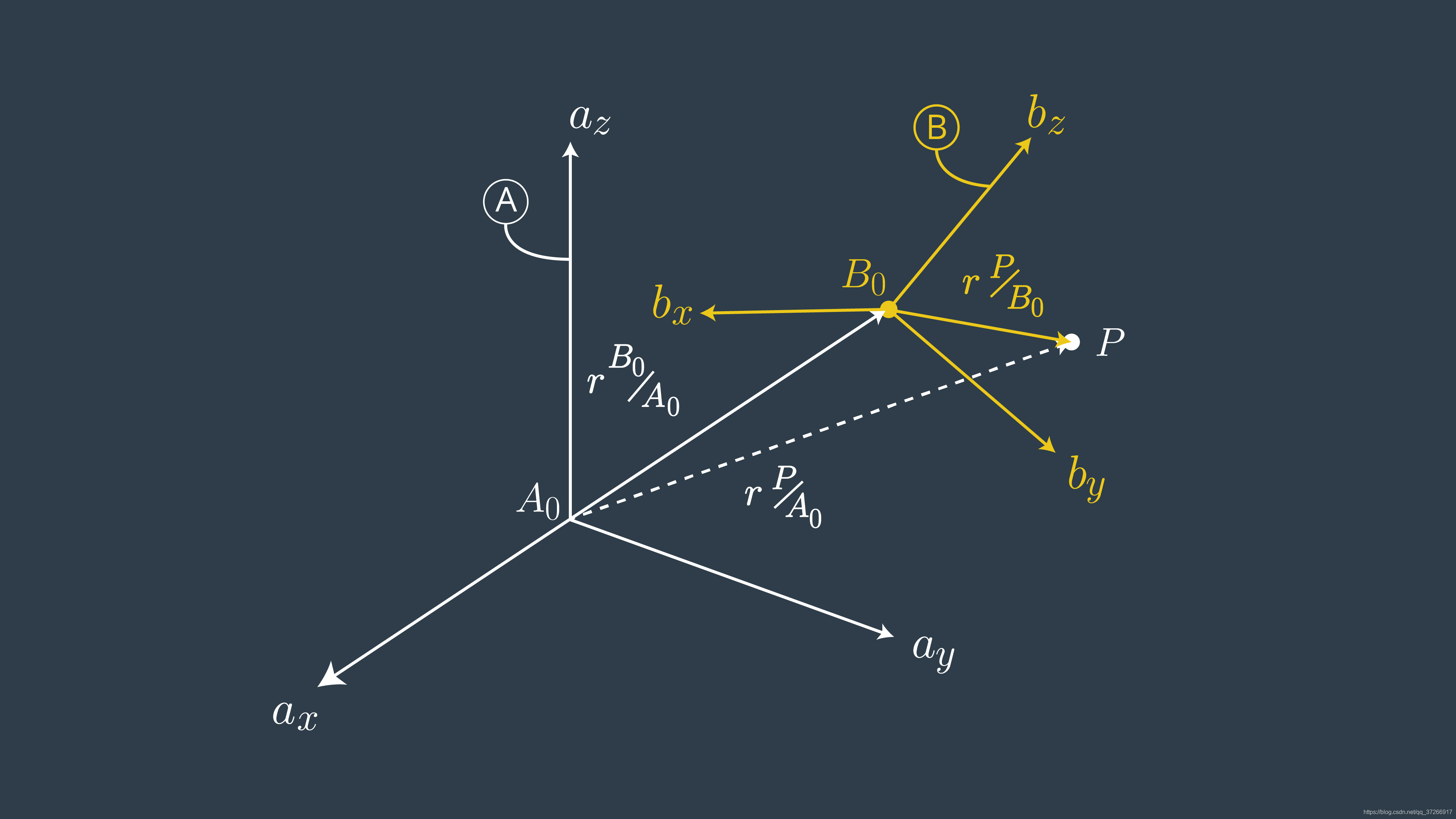
解决办法是先表达向量${}^B\mathbf{r}P/Bo$,通过在B和A坐标系之间应用一个旋转矩阵，然后加上$B_0$相对于$A_0$的偏移量。

${}^{\mathbf{A}}{\mathbf{r}}_{\mathbf{P}/{\mathbf{A}}_0}{=}_{\mathbf{B}}^{\mathbf{A}}{\mathbf{R}}^{\mathbf{B}}{\mathbf{r}}_{\mathbf{P}/{\mathbf{B}}_0}{+}^{\mathbf{A}}{\mathbf{r}}_{{\mathbf{B}}_0/{\mathbf{A}}_0}$ (1)

虽然上面的方程简洁易懂，但不便于计算机操作。然而，可以使用齐次坐标将方程(1)转换为矩阵形式，然后使用许多编程语言中可用的强大的线性代数库。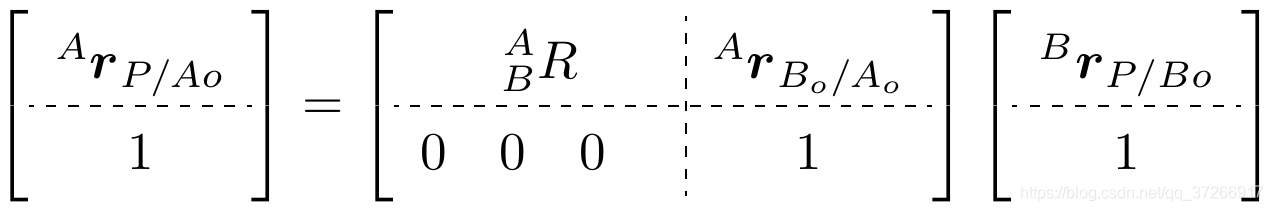
（2）

方程(2)是下面方程(3)的简写形式。
左边是一个4x1向量，它的前三个元素是点P在a坐标系中的x,y,z坐标。等式右边的第一项是4x4矩阵，称为齐次变换;它由四个子部分组成。 ${}_B^{A}R$是3x3旋转矩阵。${}^A{\mathbf{r}}_{B_0/A_0}$ 为3x1向量，表示_B坐标系相对于a坐标系的原点，用a坐标系表示。

由于矩阵乘法的维数限制，右边的最后一项也必须是4x1向量，其中 ${}^B\mathbf{r}P/B_0$是_P相对于 $B_0$并以B坐标系表示。

齐次变换的表示法类似于旋转矩阵的表示法，大写“T”(表示变换)用于前导的上标和下标。例如，${}_B^{A}T$是A和B之间的齐次变换。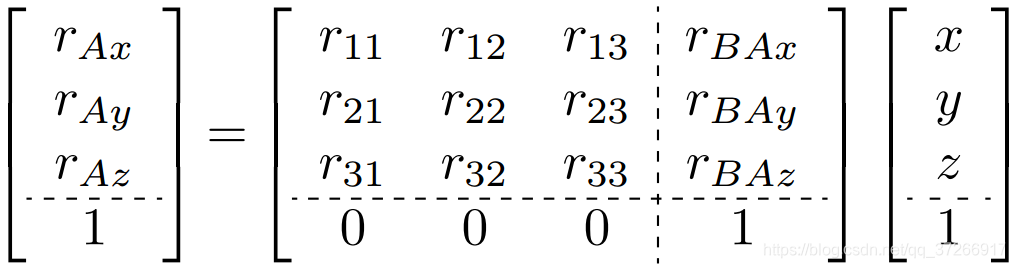
(3)

将右边的两个矩阵相乘，就可以清楚地看到矩阵形式与原始方程(1)之间的关系。

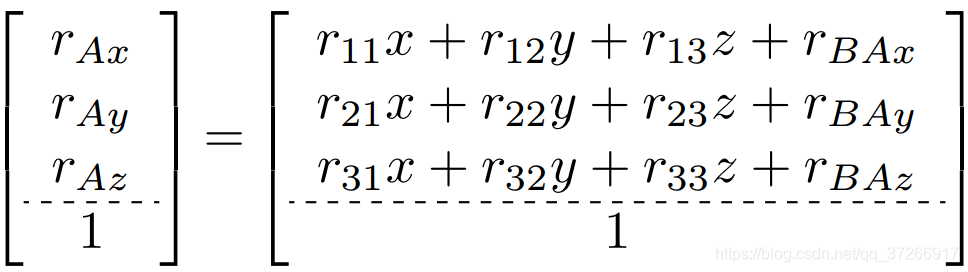
(4)

我们可以利用齐次变换的知识来计算机器人手臂末端执行器的位置。给定点P相对于参照系C的初始位置，如下。给定图像中的旋转和平移，这个点相对于坐标系B的位置是多少?

回想一下上节课，平移的偏移量是从新的坐标系的角度计算的，在例子中是参考坐标系B，因此平移量在正z方向上是34个单位。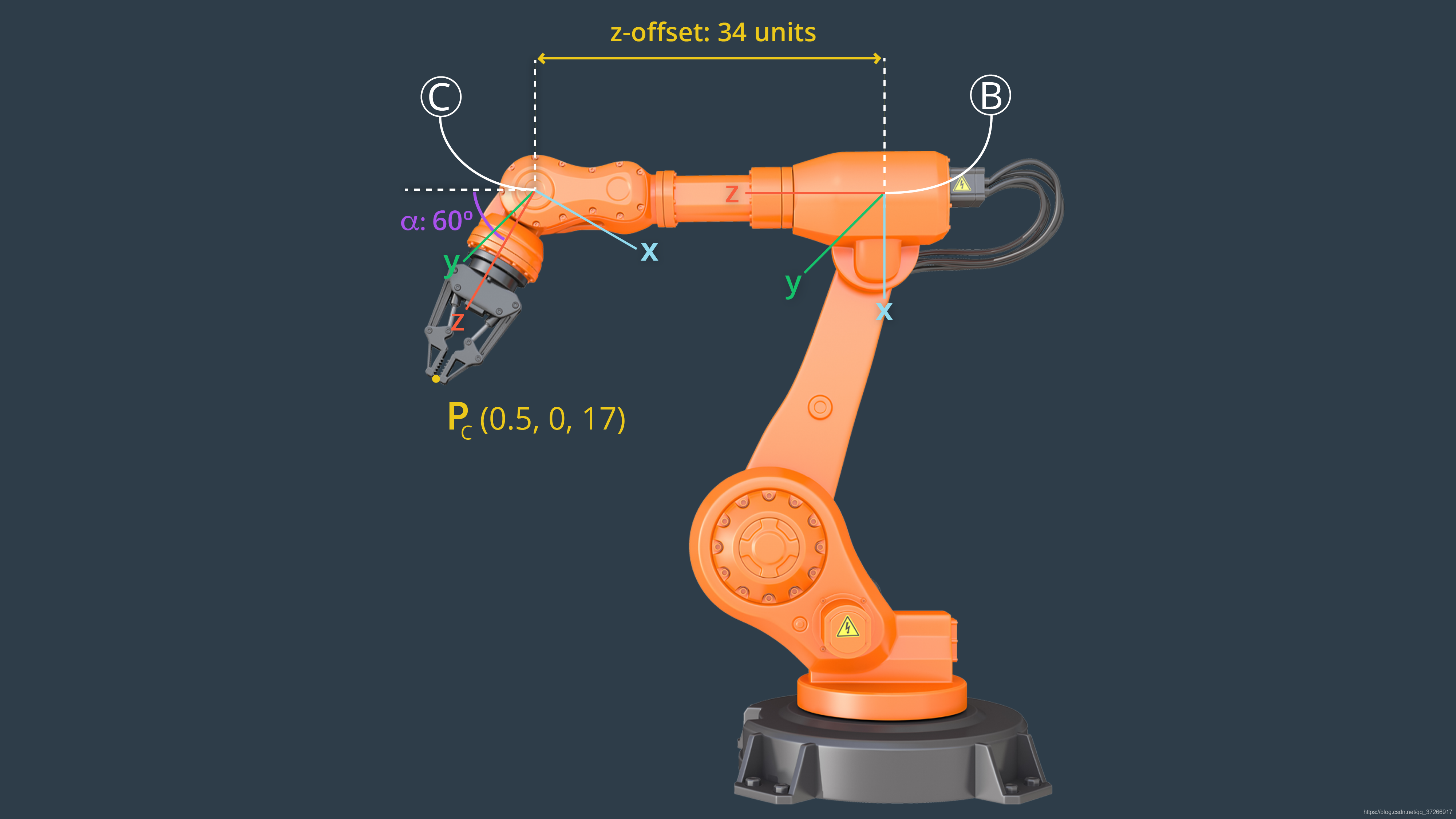

第一步是建立齐次变换矩阵从到包含绕y轴旋转60度，沿z轴平移34单位。接下来，我们将齐次变换乘以一个包含点P(0.5, 0,17)位置的矩阵。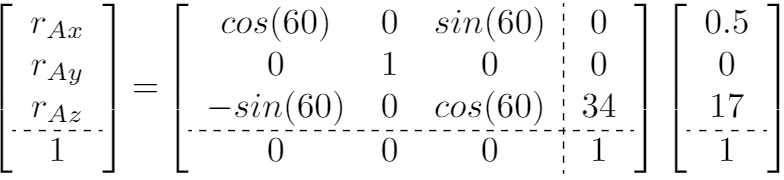

把方程右边乘出来，得到下面的结果。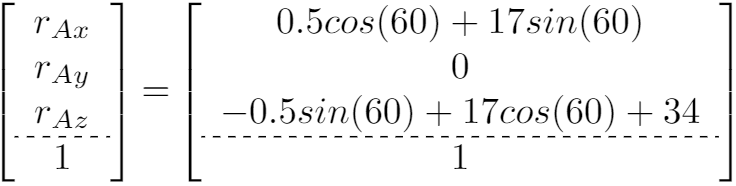

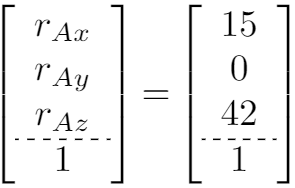
然后将点P相对于参照系B的位置粗四舍五入为(15,0,42)。

现在我们知道了末端执行器P相对于坐标系B的位置，可以再继续应用另一个变换来计算它相对于坐标系A的位置。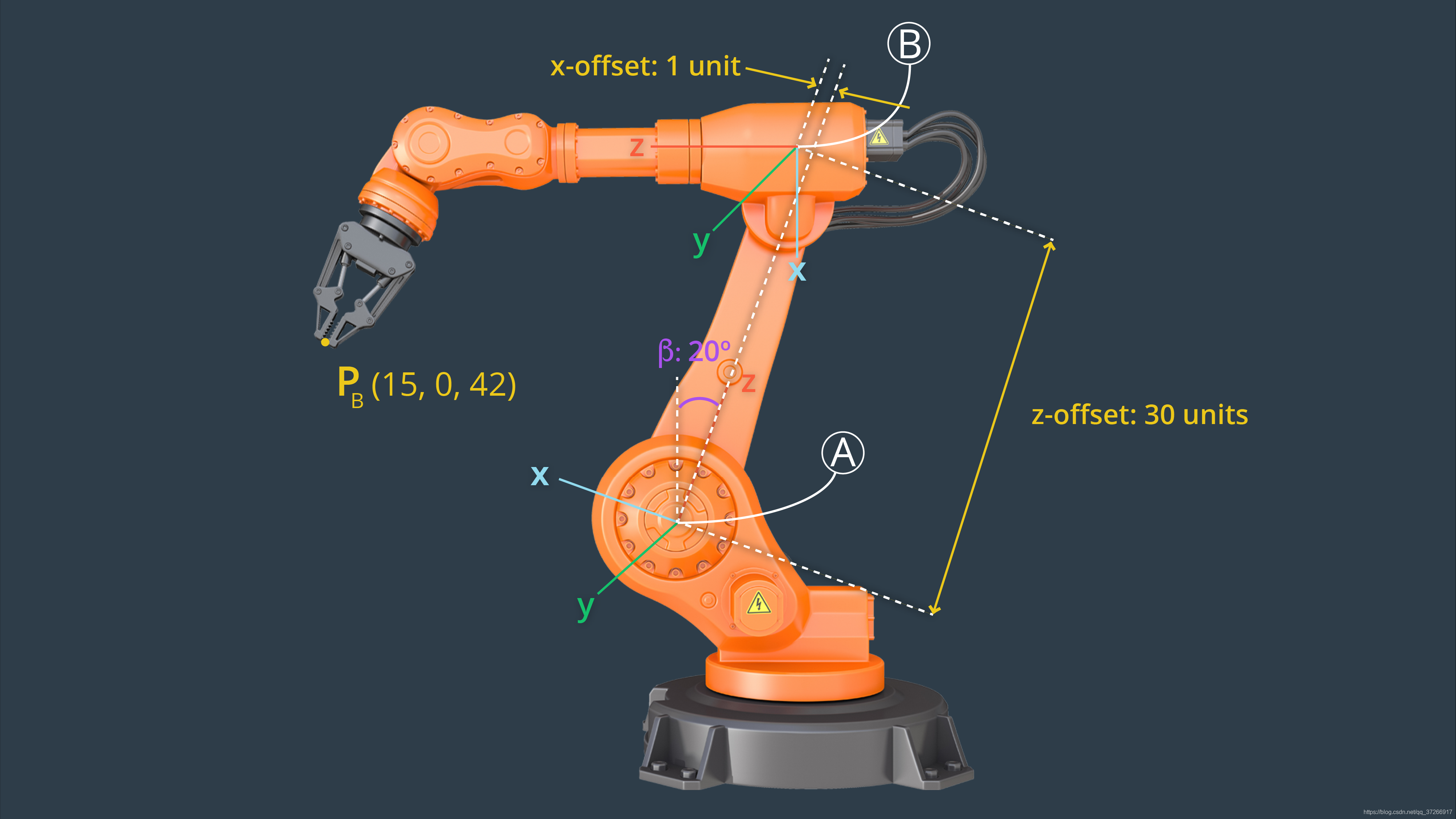

以下代码计算P相对于A坐标系的位置。

from sympy import symbols, cos, sin, pi, simplify, sqrt, atan2
from sympy.matrices import Matrix

# 转换因子
rtd = 180./pi # radians to degrees
dtr = pi/180. # degrees to radians

# 创建旋转角度的符号
q1 = symbols('q1')

# 构建 P in {B}
P = Matrix([[15.0],[0.0],[42.0],[1]])

# 定义齐次变换
T = Matrix([[ cos(q1),   0,  sin(q1),    1.],
            [ 0,         1,        0,    0.],
            [ -sin(q1),  0,  cos(q1),   30.],
            [ 0,       0,          0,   1 ]])

# 计算P在{A}中的新坐标
P_new = simplify(T * P)
print("P_new is :", P_new)

# 评价数值
print("The new coordinates of P_A are :", P_new.evalf(subs={q1: 110*dtr}))

输出为：

P_new is : Matrix([[42.0*sin(q1) + 15.0*cos(q1) + 1.0], [0], [-15.0*sin(q1) + 42.0*cos(q1) + 30.0], [1]])
The new coordinates of P_A are : Matrix([[35.3367879231231], [0], [1.53976466853328], [1.00000000000000]])