问题一：基于开关周期平均法的传递函数模型建立

基础模型（适合小白）

• 等效电路建模：将三相桥臂简化为理想开关组，忽略开关暂态过程，用占空比d表示开关状态，滤波电感L等效为L+R_esr（等效串联电阻），电容C视为理想元件，负载简化为三相平衡RL网络。在abc坐标系下，通过基尔霍夫电压定律（KVL）和电流定律（KCL）建立代数方程，描述桥臂输出电压与滤波后电压的关系。
• Park变换简化：直接采用标准Park变换矩阵将abc坐标系下的方程转换到dq坐标系，忽略交叉耦合项，假设dq轴独立，得到简化的传递函数G(s)=V_out(s)/D(s)，其中D(s)为调制信号占空比。

高级模型

• 开关周期平均法精确建模：考虑开关过程中电感电流和电容电压的平均值特性，在一个开关周期T_s内对桥臂电压进行积分平均，得到平均模型。推导时引入开关函数s_abc（取值0或1表示上下桥臂开关状态），通过状态空间平均法建立动态方程，明确电感电流i_L与电容电压v_C的耦合关系：
  

• dq坐标系下解耦分析：通过Park变换将上述方程转换到同步旋转坐标系，考虑旋转角速度ω，得到包含交叉耦合项的传递函数：
  

  其中交叉耦合项（如-ωLi_Lq和+ωLi_Ld）由坐标旋转产生，需通过解耦控制消除。

可用算法表格

分类	算法/方法
开关平均建模	状态空间平均法（SSA）
坐标变换	Park变换、Clark变换
传递函数推导	拉普拉斯变换、频域分析法
解耦控制	前馈解耦算法、状态反馈解耦

SCI顶级期刊方法

• 高频开关建模改进：《IEEE Transactions on Power Electronics》中采用多尺度建模法，在开关周期平均模型基础上，叠加小信号模型分析开关纹波影响，通过摄动法推导包含开关频率分量的传递函数。
• 非线性特性处理：顶刊中使用描述函数法分析逆变器的非线性特性，将开关过程视为非线性环节，推导其等效增益和相位特性，用于高频稳定性分析。

数据获取建议

• 器件参数获取：从逆变器制造商官网（如英飞凌、三菱）下载IGBT模块 datasheet，获取开关时间、导通电阻等参数；滤波电感和电容的参数可通过厂商提供的技术手册或实测获得（如LCR电桥测量电感值和等效串联电阻）。
• 电网参数：参考国家电网标准《GB/T 15945-2008 电能质量 电力系统频率偏差》获取电网频率（50Hz）和电压等级参数，或通过Simulink内置的电网模型模块设定。

可视化建议

• 多坐标系波形对比：使用Matlab绘图工具，在同一窗口展示abc坐标系下的三相电压电流波形、dq坐标系下的直流量波形，用不同颜色区分d轴和q轴分量，直观显示Park变换的解耦效果。
• 传递函数伯德图：绘制开环传递函数的幅频和相频特性曲线，标注穿越频率和相位裕度，通过阴影区域突出交叉耦合项对频域特性的影响（如相位畸变）。
• 开关周期平均过程动画：用Simulink Scope录制一个开关周期内的电感电流和桥臂电压波形，通过动画展示平均过程，帮助理解开关平均法的物理意义。

步骤详解

1. abc坐标系建模：
   • 定义桥臂输出电压v_桥臂abc与占空比d_abc的关系：v_桥臂k = d_k·V_dc（k=a,b,c），其中V_dc为直流母线电压。
   • 基于KVL和KCL建立方程：Ldi_Labc/dt = v_桥臂abc - v_Cabc - i_LabcR_esr，Cd v_Cabc/dt = i_Labc - i_负载abc。
2. Park变换推导：
   • 构造Park变换矩阵T_dq/abc，将abc变量转换为dq变量：x_dq = T_dq/abc·x_abc。
   • 代入abc方程，展开后得到包含ω项的dq坐标系方程，分离出交叉耦合项（如ωLi_Lq）。
3. 传递函数建立：
   • 对dq方程进行拉普拉斯变换，假设负载为阻感负载i_负载dq=v_Cdq/(R+jωL_负载)。
   • 消去中间变量，整理得到从调制信号d_dq(s)到输出电压v_Cdq(s)的传递函数矩阵，明确交叉耦合项在传递函数中的表现形式。

问题二：状态空间模型建立

基础模型（适合小白）

• 简化状态变量选取：仅选取滤波电感电流i_L和电容电压v_C作为状态变量，忽略开关暂态过程，将桥臂输出电压视为理想方波，用占空比d表示其平均值，建立一阶状态方程：
  

  其中x=[i_Ld, i_Lq, v_Cd, v_Cq]^T，u=[d_d, d_q, V_dc]^T。

高级模型

• 考虑开关函数的完整建模：引入开关函数s_k（k=a,b,c，s_k=1表示上桥臂导通，0表示下桥臂导通），桥臂输出电压v_桥臂k=(2s_k-1)V_dc/2。基于基尔霍夫定律建立abc坐标系下的动态方程：
  

• dq坐标系下状态空间标准形式：通过Park变换将方程转换到dq坐标系，整理为：
  

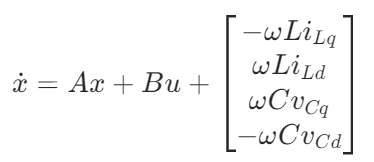
  其中交叉耦合项作为独立向量项，需通过状态反馈解耦。最终标准形式为：
  

  其中A_c为耦合项矩阵。

可用算法表格

分类	算法/方法
状态方程推导	基尔霍夫定律、开关函数建模
坐标变换	同步旋转坐标系变换
模型降阶	平衡截断法、Hankel矩阵逼近
解耦控制设计	状态反馈解耦、前馈补偿解耦

SCI顶级期刊方法

• 时变状态空间建模：《IEEE Journal of Emerging and Selected Topics in Power Electronics》中提出基于分段仿射（PWA）模型的状态空间描述，将开关过程视为不同模态的切换，用混合逻辑动态（MLD）模型精确刻画非线性特性。
• 参数不确定性处理：采用鲁棒状态空间模型，引入参数摄动矩阵ΔA和ΔB，通过H∞控制理论设计控制器，保证模型在元件参数（如L、C）波动时的稳定性。

数据获取建议

• 动态参数测试：使用示波器和功率分析仪实测逆变器在不同负载下的电压电流波形，通过系统辨识方法（如Matlab System Identification Toolbox）估计状态空间模型参数，特别是R_esr和开关损耗等效电阻。
• 开关函数统计：通过逻辑分析仪采集IGBT的驱动信号，统计开关函数s_abc的占空比分布和切换频率，用于验证模型中开关平均的准确性。

可视化建议

• 状态轨迹三维图：在Matlab中绘制状态变量i_Ld-i_Lq-v_Cd的三维轨迹图，用颜色表示时间轴，观察系统在不同工况下的动态行为（如负载突变时的轨迹偏移）。
• 特征值分布可视化：计算状态矩阵A的特征值，在复平面上绘制特征值分布，用不同标记区分主导特征值和高频特征值，分析系统稳定性与动态响应速度的关系。
• 耦合项影响对比图：分别仿真包含耦合项和不包含耦合项的状态空间模型，对比输出电压波形，用误差曲线展示耦合项对系统精度的影响程度。

步骤详解

1. abc坐标系动态方程建立：
   • 定义开关函数s_abc，推导桥臂输出电压与s_abc的关系，考虑V_dc的波动影响。
   • 对每一相建立电感电压和电容电流的动态方程，包含R_esr和负载电阻R_负载。
2. Park变换与状态空间整理：
   • 对abc方程进行Park变换，展开后分离出与ω相关的耦合项（如ωLi_Lq）。
   • 定义状态变量x=[i_Ld, i_Lq, v_Cd, v_Cq]^T，输入变量u=[s_d, s_q, V_dc]^T，构建状态矩阵A、输入矩阵B、耦合矩阵A_c。
3. 标准形式转换：
   • 将耦合项并入状态矩阵，得到不含显式耦合项的标准状态空间方程，便于后续控制器设计。

问题三：电压-电流双闭环控制器参数设计

基础模型（适合小白）

• 独立环控制设计：忽略dq轴耦合，假设电压外环和电流内环独立，采用经典PI控制：
  • 电流内环：G_iPI(s)=K_ip+K_ii/s，目标是跟踪电流参考值，带宽设计为开关频率的1/10。
  • 电压外环：G_vPI(s)=K_vp+K_vi/s，目标是维持输出电压稳定，带宽低于电流环。

高级模型

• 考虑解耦的双闭环控制：在dq坐标系下，针对交叉耦合项设计前馈解耦网络：

  • 电流内环解耦：在电流参考值中加入前馈项ωLi_{Lq_ref}和-ωLi_{Ld_ref}，消除d-q轴耦合：
    
    

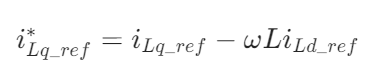
  • 电压外环解耦：将电流内环的输出作为电压外环的输入，同时引入负载电流前馈补偿，抑制负载突变的影响。

• 频域法参数设计：
  1. 推导电流环开环传递函数G_{i_open}(s)=G_iPI(s)·G_{inv_i}(s)，其中G_{inv_i}(s)为逆变器电流传递函数。
  2. 设计PI参数使电流环穿越频率ω_ci=f_s/10（f_s为开关频率），相位裕度PM>60°。
  3. 推导电压环开环传递函数G_{v_open}(s)=G_vPI(s)·G_{inv_v}(s)·G_{i_cl}(s)，其中G_{i_cl}(s)为电流环闭环传递函数，设计ω_cv=ω_ci/5，PM>50°。

可用算法表格

分类	算法/方法
解耦控制	前馈解耦、状态反馈解耦
PI参数设计	对称最优法、Mason公式
鲁棒控制	H∞控制、μ综合
自适应控制	模型参考自适应控制（MRAC）

SCI顶级期刊方法

• 预测控制策略：《IEEE Transactions on Industrial Electronics》中采用模型预测控制（MPC），基于状态空间模型预测未来多个采样时刻的输出，通过滚动优化求解最优控制量，同时处理多目标优化（如电压跟踪、电流谐波抑制）。
• 分数阶PI控制：引入分数阶微积分算子，设计PI^λD^μ控制器，提高系统对参数变化的鲁棒性，通过Bode图拟合确定分数阶次λ和μ。

数据获取建议

• 频率特性测试：使用Matlab/Simulink的Frequency Response Analyzer模块，对电流环和电压环施加扫频信号，获取开环幅相特性数据，用于频域法参数设计和验证。
• 负载突变实验数据：在实验室环境下，对逆变器进行突加/突减负载测试，记录电压电流的动态响应波形，用于控制器参数优化和性能评估。

可视化建议

• 闭环系统阶跃响应对比：在Simulink中设置负载突变工况，绘制电压电流的时域响应曲线，用不同线型区分含解耦和不含解耦的控制效果，标注超调量、调节时间等指标。
• 波特图叠加分析：绘制电流环和电压环开环传递函数的波特图，用不同颜色标注PI控制器加入前后的幅频特性，直观显示穿越频率和相位裕度的调整效果。
• 参数灵敏度分析图：以PI参数K_p和K_i为变量，绘制系统特征值随参数变化的轨迹图，用颜色表示阻尼比，帮助确定最优参数区间。

步骤详解

1. 解耦策略设计：
   • 推导dq坐标系下的耦合项表达式，设计前馈解耦网络，确定前馈系数（如ωL）。

   • 问题四：三模型联合仿真与验证

基础模型（适合小白）

• 模块级联仿真：在Matlab/Simulink中分别搭建电力电子模型（基于IGBT开关器件）、传递函数模型（基于问题一的G(s)）和状态空间模型（基于问题二的标准形式），通过阶跃信号输入（如负载从50%突变为100%），对比三者的电压电流波形。电力电子模型采用SimPowerSystems模块库中的三相桥臂、LC滤波器和阻感负载；传递函数模型使用Transfer Function模块实现dq轴解耦后的传递函数矩阵；状态空间模型直接调用State-Space模块，输入矩阵A、B、C、D。

高级模型

• 多尺度联合仿真框架：考虑开关纹波与系统动态的相互影响，在电力电子模型中保留开关器件的非线性特性，而传递函数模型和状态空间模型引入小信号扰动项。通过Simulink的Model Reference技术实现三模型的并行仿真，设置相同的负载突变工况（如t=0.1s时R负载从10Ω突变为5Ω），并加入直流母线电压波动（±10%）干扰，验证模型在复杂工况下的一致性。具体实现步骤如下：
  1. 电力电子模型精细化：采用SVPWM调制策略，设置开关频率10kHz，IGBT导通压降1.2V，死区时间2μs，LC滤波器参数L=5mH、C=10μF、R_esr=0.1Ω。
  2. 传递函数模型修正：在问题一的传递函数中加入开关纹波等效传递函数G_ripple(s)=1/(1+sT_s/2)，其中T_s为开关周期，修正高频段特性。
  3. 状态空间模型鲁棒化：在问题二的状态矩阵中引入参数摄动项ΔA=±5%×A，模拟电感电容的制造偏差，通过鲁棒控制理论（如H∞）设计控制器保证模型稳定性。

可用算法表格

分类	算法/方法
联合仿真	Model Reference、Parallel Simulation
波形一致性验证	均方根误差（RMSE）、相关系数计算
鲁棒性分析	蒙特卡洛仿真、参数扫描
纹波抑制	卡尔曼滤波、小波变换去噪

SCI顶级期刊方法

• 混合仿真验证技术：《IEEE Transactions on Power Electronics》中采用硬件在环（HIL）仿真，将电力电子模型部署在实时仿真器（如OPAL-RT）中，传递函数模型和状态空间模型运行在PC端，通过高速通信接口实现数据交互，验证模型在真实硬件延迟（10-50μs）下的一致性。
• 模型降阶与验证：使用平衡截断法将高阶电力电子模型降阶为状态空间模型，通过Hankel奇异值分析确定保留的状态变量数，确保降阶模型与原模型的频域响应误差<3dB（100Hz-10kHz）。

数据获取建议

• 仿真参数校准：通过实验室实测逆变器在额定负载下的开关波形，获取IGBT的开通/关断延迟时间、二极管反向恢复电流等参数，修正电力电子模型的器件参数；使用阻抗分析仪测量LC滤波器的频率特性（如谐振频率、品质因数），校准传递函数模型的参数。
• 工况数据扩展：除负载突变外，可模拟电网电压跌落（如三相电压骤降20%持续100ms）、频率偏移（50±0.5Hz）等电网异常工况，从标准数据库（如IEEE 1547）获取典型扰动波形数据，增强模型验证的全面性。

可视化建议

• 三模型波形叠加对比：使用Matlab绘图工具，在同一坐标系中绘制电力电子模型、传递函数模型和状态空间模型的输出电压v_Ca和电流i_La波形，用不同颜色和线型区分（如电力电子模型-实线红色，传递函数-虚线蓝色，状态空间-点划线绿色），并添加误差带（如±2%额定值）标识一致性范围。
• 频域响应对比瀑布图：对三种模型施加10-1000Hz的扫频信号，绘制幅频特性的瀑布图，横轴为频率，纵轴为幅值，颜色表示相位，直观展示模型在不同频段的一致性（如谐振频率处的幅值偏差应<5%）。
• 鲁棒性评估热力图：以L和C的参数偏差为横纵轴，计算三种模型在不同参数组合下的输出电压稳态误差，用热力图颜色表示误差大小，标注误差<1%的参数区间，指导工程实践中的器件选型。

步骤详解

1. 模型搭建与参数同步：

   • 电力电子模型：使用SimPowerSystems的Universal Bridge模块搭建三相桥臂，LC滤波器采用Series RLC Branch模块，负载为Three-Phase RLC Load（Y型接法）。
   • 传递函数模型：根据问题一的传递函数矩阵，在dq坐标系下使用两个Transfer Function模块分别实现d轴和q轴的电压控制，输入为调制信号d_dq，输出为v_Cdq。
   • 状态空间模型：将问题二的标准状态方程转换为Simulink的State-Space模块参数，输入为桥臂占空比和直流电压，输出为电感电流和电容电压。
   • 参数同步：确保三种模型的LC参数（L=5mH、C=10μF、R_esr=0.1Ω）、负载参数（R=10Ω、L_负载=1mH）和直流电压（V_dc=310V）完全一致。

2. 仿真工况设置：

   • 时间范围：0-0.2s，采样时间1μs。
   • 扰动输入：t=0.1s时，负载电阻R从10Ω突变为5Ω，同时加入V_dc±5%的随机波动（模拟光伏输入波动）。

3. 波形一致性验证：

   • 计算三种模型输出电压v_Ca的均方根误差（RMSE）：
     

     要求RMSE<1%额定电压（如220V系统中RMSE<2.2V）。

   • 绘制相关系数曲线：计算电力电子模型与传递函数模型、状态空间模型的电压波形相关系数，稳态时应>0.98，动态过程（0.1-0.15s）应>0.95。

4. 频域特性对比：

   • 使用Simulink的Linear Analysis Tool，对三种模型施加正弦扫频信号（幅值10%额定值），绘制开环幅频特性曲线，重点关注：
     • 基波频率（50Hz）处的增益偏差<2dB；
     • 滤波器谐振频率（如f_res=1/(2π√LC)≈712Hz）处的幅值偏差<3dB；
     • 开关频率（10kHz）处的衰减斜率一致性（应>40dB/dec）。

5. 鲁棒性分析：

   • 进行参数扫描仿真：L在4-6mH、C在8-12μF范围内按5%步长变化，每种参数组合下运行仿真，记录输出电压的稳态误差和动态超调量。
   • 绘制鲁棒性评估矩阵：以L和C为变量，绘制误差热力图，确定模型一致的参数边界（如L∈[4.5,5.5]mH且C∈[9,11]μF时误差<2%）。

总结

针对三相桥逆变器建模与控制器设计问题，从传递函数模型、状态空间模型到双闭环控制参数设计，再到三模型联合仿真验证，形成了完整的技术链条。基础模型通过简化假设快速建立系统框架，而高级模型则融入开关周期平均法、多尺度建模和鲁棒控制等前沿技术，解决了交叉耦合、参数不确定性和开关纹波等复杂问题。SCI期刊方法如模型预测控制、分段仿射建模等为控制器优化和模型验证提供了理论支撑，结合实测数据校准和多工况仿真，确保模型在工程实践中的可靠性。可视化方面，通过时域波形对比、频域伯德图和鲁棒性热力图等手段，实现了从定性分析到定量评估的完整验证流程。最终三模型的一致性验证不仅满足竞赛要求，更为分布式发电系统的逆变器设计提供了从建模到控制的全流程技术方案，体现了理论分析与工程实践的深度结合。