2025 | 浙大团队开源π³模型！视觉几何重建新突破，性能碾压VGGT！

本论文提出的π³是一种完全置换等变的前馈神经网络，通过预测仿射不变相机姿态和尺度不变局部点图，打破了视觉几何重建对固定参考视图的依赖。该模型在相机姿态估计、点图估计、视频深度估计和单目深度估计等多项任务中，在RealEstate10K、Sintel、KITTI等多个数据集上均取得了SOTA或可比性能，同时具有输入顺序鲁棒性强、可扩展性好、收敛速度快等优势。

CV实验室

1587人浏览 · 2025-07-28 16:13:18

CV实验室 · 2025-07-28 16:13:18 发布

论文基本信息

论文标题：π³: Scalable Permutation-Equivariant Visual Geometry Learning
作者：Yifan Wang, Jianjun Zhou, Haoyi Zhu, Wenzheng Chang, Yang Zhou, Zizun Li, Junyi Chen, Jiangmiao Pang, Chunhua Shen, Tong He（标注*的为同等贡献作者，标注†的为通讯作者）
作者单位：Shanghai AI Lab，ZJU，SII
论文链接：https://arxiv.org/abs/2507.13347
项目链接：https://yyfz.github.io/pi3/
另外我整理了CVPR 2025 计算机视觉相关论文合集+源码，感兴趣的 d d 我~
论文这里~

2. 【论文速读】

π3 effectively reconstructs a diverse set of open-domain images in a feed-forward manner, encompassing various scenes such as indoor, outdoor, and aerial-view, as well as cartoons, with both dynamic and static content

来自上海AILab和浙江大学的研究人员最近提出了了π³，这是一种前馈神经网络，它为视觉几何重建提供了一种新颖方法，打破了对传统固定参考视图的依赖。以往的方法通常将重建结果锚定在指定视角上，这种归纳偏置在参考视图不理想时可能导致不稳定性和重建失败。与之不同的是，π³采用完全置换等变架构，无需任何参考框架就能预测仿射不变的相机姿态和尺度不变的局部点图。这种设计使该模型本身对输入顺序具有鲁棒性，且扩展性极强。这些优势使其这种简单且无偏的方法在众多任务中达到了最先进的性能，包括相机姿态估计、单目/视频深度估计以及密集点图重建。

3.【研究背景及相关工作】

3.1 研究背景

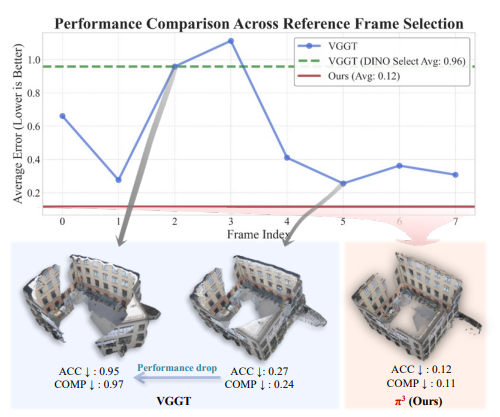
视觉几何重建在增强现实、机器人等领域应用广泛。传统方法依赖迭代优化，前馈神经网络（如DUSt3R）虽有进展，但传统与现代方法均依赖固定参考视图，将其相机坐标系作为全局参考框架，这一归纳偏置限制了模型性能与鲁棒性，参考视图选择不佳会导致重建质量下降。

3.2 相关工作

3.2.1 传统3D重建

SfM和MVS等经典方法通过多视图几何建立特征对应，估计相机姿态并生成3D点云，但依赖复杂多阶段流程和耗时的迭代优化（如Bundle Adjustment）。

3.2.2 前馈3D重建

前馈模型可直接从图像回归3D结构。Dust3R处理图像对但扩展需全局对齐；Fast3R支持多图推理，FLARE分解任务，VGGT利用多任务学习，不过这些方法均需将3D结构锚定到参考框架。

Performance comparison across different reference frames.

4.【方法论】

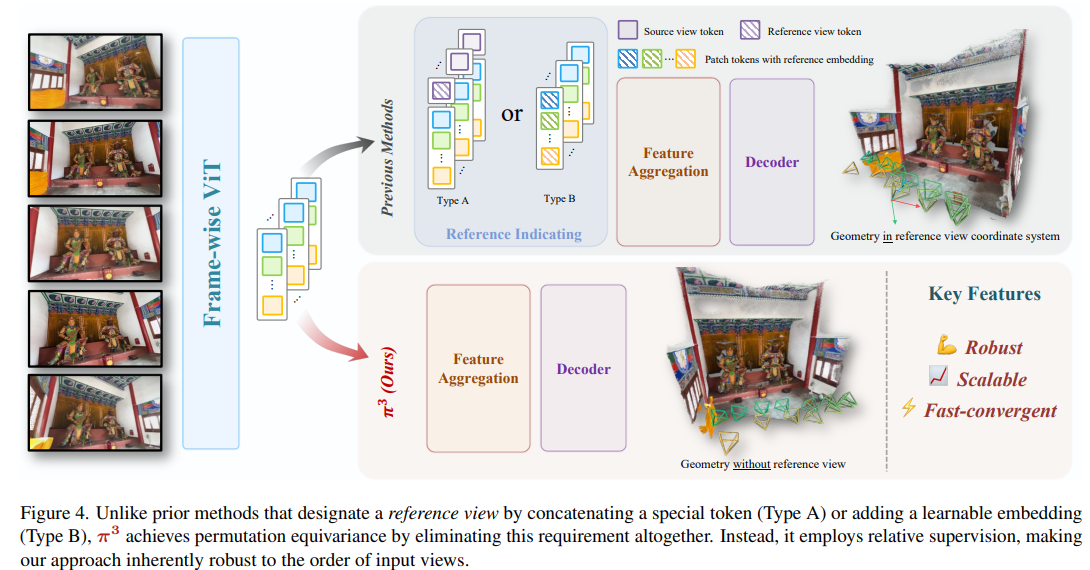
Unlike prior methods that designate a reference view by concatenating a special token (Type A) or adding a learnable embedding (Type B)

4.1 置换等变架构（Permutation-Equivariant Architecture）

核心设计目标：确保模型输出不受输入视图顺序的影响，实现对输入排序的稳健性。
输入与输出映射：设输入为N幅图像序列 $S=(I_{1}, ..., I_{N})$ （每幅图像 $I_{i} \in \mathbb{R}^{H ×W ×3}$ ），网络 $\phi$ 将其映射为输出序列元组：
$\phi(S)=\left(\left(T_{1}, ..., T_{N}\right),\left(X_{1}, ..., X_{N}\right),\left(C_{1}, ..., C_{N}\right)\right)$
其中， $T_{i} \in SE(3) \subset \mathbb{R}^{4×4}$ 为相机姿态， $X_{i} \in \mathbb{R}^{H×W×3}$ 为像素对齐的3D点图（自身相机坐标系下）， $C_{i} \in \mathbb{R}^{H×W}$ 为点图的置信度图。
置换等变性质：对任意置换算子 $P_{\pi}$ ，满足 $\phi\left(P_{\pi}(S)\right)=P_{\pi}(\phi(S))$ ，即输入序列置换后，输出序列也发生相同置换，保证图像与输出的一一对应关系。
实现方式：省略位置嵌入、参考视图标记等顺序相关组件；通过DINOv2骨干网生成补丁标记，经交替的视图级和全局自注意力层处理后，由解码器输出结果。

4.2 尺度不变局部几何（Scale-Invariant Local Geometry）

几何表示：为每幅图像 $I_{i}$ 预测3D点图 $\hat{X}_{i}$ ，点云在自身局部坐标系中定义，且所有图像共享一个未知但一致的缩放因子，解决单目重建的尺度模糊问题。
尺度对齐优化：通过求解最优缩放因子 $s^{*}$ 对齐预测点图与真值：
$s^{*}=\underset{s}{arg min } \sum_{i=1}^{N} \sum_{j=1}^{H × W} \frac{1}{z_{i, j}}\left\| s \hat{x}_{i, j}-x_{i, j}\right\| _{1}$
其中 $z_{i,j}$ 为真值深度，该问题通过ROE求解器解决。
损失函数：
- 点云重建损失： $\mathcal{L}_{points }=\sum_{i=1}^{N} \sum_{j=1}^{H × W} \frac{1}{z_{i, j}}\left\| \hat{s} \hat{x}_{i, j}-x_{i, j}\right\| _{1}$
- 法向量损失（鼓励表面平滑）： $\mathcal{L}_{normal }=\sum_{i=1}^{N} \sum_{j=1}^{H × W} arccos \left(\hat{n}_{i, j} \cdot n_{i, j}\right)$
- 置信度损失（BCE损失）：基于重建误差阈值判断置信度目标值。

4.3 仿射不变相机姿态（Affine-Invariant Camera Pose）

姿态模糊性：相机姿态 $(\hat{T}_{1}, ..., \hat{T}_{N})$ 仅在相似变换（刚性变换+全局缩放）下有定义。
相对姿态监督：通过视图间相对姿态消除全局参考框架模糊，相对姿态计算为：
$\hat{T}_{i \leftarrow j}=\hat{T}_{i}^{-1} \hat{T}_{j}$
其中旋转分量 $\hat{R}_{i \leftarrow j}$ 不受全局变换影响，平移分量通过尺度因子 $\hat{s}$ 校正。
相机损失函数：
$\mathcal{L}_{cam }=\frac{1}{N(N-1)} \sum_{i \neq j}\left(\mathcal{L}_{rot }(i, j)+\lambda \mathcal{L}_{trans }(i, j)\right)$
- 旋转损失（测地距离）： $\mathcal{L}_{rot }(i, j)=arccos \left(\frac{Tr\left(\left(R_{i \leftarrow j}\right)^{\top} \hat{R}_{i \leftarrow j}\right)-1}{2}\right)$
- 平移损失（Huber损失，抗噪）： $\mathcal{L}_{trans }(i, j)=\mathcal{H}_{\delta}\left(s^{*} \hat{t}_{i \leftarrow j}-t_{i \leftarrow j}\right)$ 。

4.4 模型训练（Model Training）

复合损失函数：通过加权求和整合多任务损失：
$\mathcal{L}=\mathcal{L}_{points }+\lambda_{normal } \mathcal{L}_{normal }+\lambda_{conf } \mathcal{L}_{conf }+\lambda_{cam } \mathcal{L}_{cam }$ 。
训练数据：在15个多样化数据集上训练，涵盖室内外、合成与真实场景，包括GTASfM、CO3D、ScanNet等。

5.【实验结果分析】

5.1 相机姿态估计（Camera Pose Estimation）

实验从角度精度和距离误差两个维度评估相机姿态预测性能，并在多个数据集上进行验证。

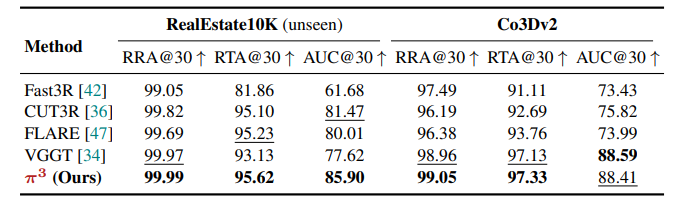
角度精度指标：在场景级的RealEstate10K（未见过的数据）和物体中心的Co3Dv2（训练时见过的数据）数据集上，通过计算相对旋转精度（RRA）、相对平移精度（RTA）及AUC值评估。结果显示，在RealEstate10K上，π³的RRA@30达99.99、RTA@30达95.62、AUC@30达85.90，创下零样本泛化的新SOTA；在Co3Dv2上性能与SOTA相当。
距离误差指标：在Sintel（合成户外）、TUM-dynamics（真实室内）和ScanNet（真实室内，训练时见过）数据集上，以绝对轨迹误差（ATE）等为指标。π³在Sintel上表现显著优于其他方法，ATE从VGGT的0.167降至0.074；在TUM-dynamics和ScanNet上与VGGT共同达到SOTA水平。

5.2 点图估计（Point Map Estimation）

在多个数据集的稀疏视图和密集视图条件下评估重建点图质量，以精度（Acc.）、完整性（Comp.）和法向量一致性（N.C.）为指标。

物体级与场景级数据集：在DTU（物体级）和ETH3D（场景级）数据集上，π³的表现优于VGGT等方法。例如在ETH3D上，π³的Acc.（Mean）为0.194，Comp.（Mean）为0.210，N.C.（Mean）为0.883，均优于VGGT的对应指标。
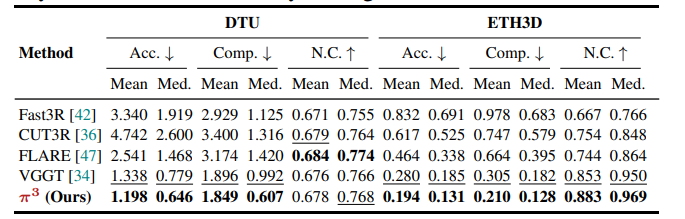
稀疏与密集视图：在7-Scenes和NRGBD数据集上，无论稀疏视图（关键帧间隔大）还是密集视图（关键帧间隔小）设置，π³均表现稳健。如NRGBD密集视图下，π³的Acc.（Mean）为0.015，Comp.（Mean）为0.013，N.C.（Mean）为0.898，性能出色。
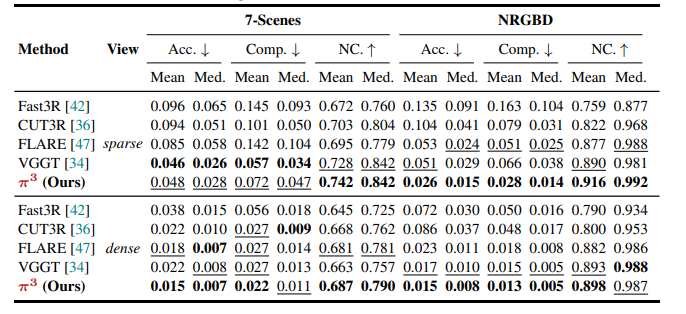
定性结果：π³重建的点图更清晰、准确、完整，伪影更少。

5.3 视频深度估计（Video Depth Estimation）

在Sintel、Bonn和KITTI数据集上，以绝对相对误差（Abs Rel）和阈值精度（δ<1.25）为指标，评估两种对齐设置（仅尺度对齐、联合尺度与3D平移对齐）下的性能。
Video Depth Estimation on Sintel, Bonn [19] and KITTI [10]

精度表现：π³在所有数据集和对齐设置下均达到新SOTA。例如在Sintel仅尺度对齐设置下，Abs Rel从VGGT的0.299降至0.233，δ<1.25从0.638提升至0.664；联合对齐设置下优势更明显。
效率：π³在KITTI上的推理速度达57.4 FPS，快于VGGT（43.2 FPS）和Aether（6.14 FPS），且模型参数更小（959M）。

5.4 单目深度估计（Monocular Depth Estimation）

在Sintel、Bonn、KITTI和NYU-v2数据集上，以Abs Rel和δ<1.25为指标评估，每个深度图独立与真值对齐。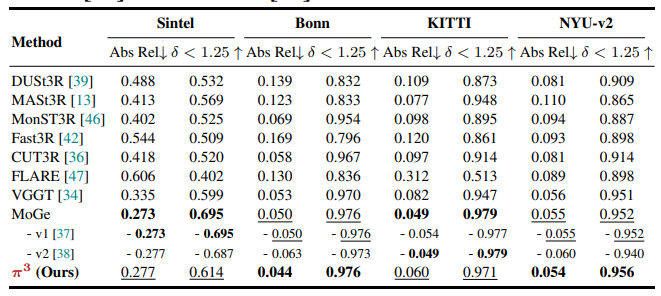
Monocular Depth Estimation on Sintel , Bonn KITTI and NYU-v2 .

结果显示，π³在多帧前馈重建方法中达到SOTA。例如在Bonn数据集上，Abs Rel为0.044，δ<1.25为0.976，与专门优化单帧深度估计的MoGe性能相当。

5.5 输入序列置换鲁棒性评估（Robustness Evaluation）

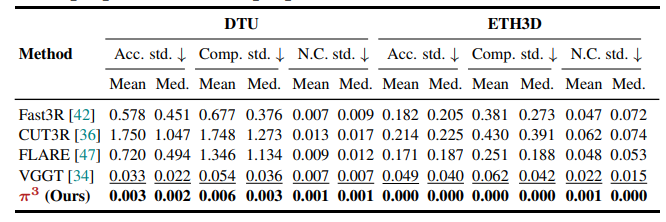
Standard Deviation of Point Cloud Estimation on DTU and ETH3D

在DTU和ETH3D数据集上，通过替换输入序列首帧并计算重建指标的标准差，评估对输入顺序的稳健性。

π³在所有指标上的标准差接近零。例如在DTU上，精度均值标准差为0.003，远低于VGGT的0.033；在ETH3D上几乎无方差，证明其置换等变性设计有效，输出不受输入顺序影响。

5.6 消融实验（Ablation Study）

以VGGT为基础构建基线模型，逐步添加尺度不变点图和仿射不变相机姿态组件，评估性能变化。

基线模型（无新增组件）的 metric 为0.1498；添加尺度不变点图后提升至0.1145；再添加仿射不变相机姿态（完整模型）后显著提升至0.0625，证明两个组件对精度和稳健性至关重要。

Qualitative comparison of in-the-wild multi-view 3D reconstruction

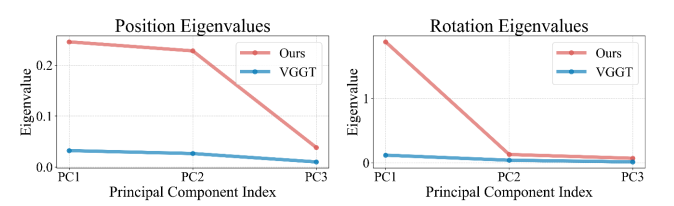
5.7 模型规模可扩展性分析（Scalability and Performance Evaluation）

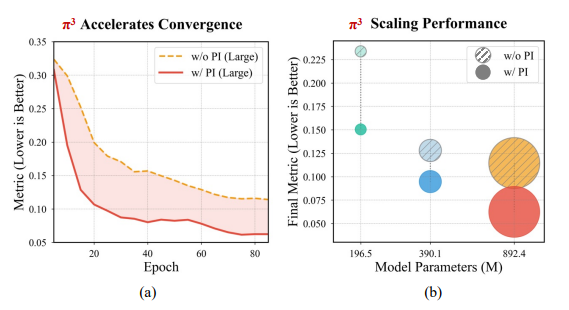
π3demonstrates significant convergence acceleration(a) and enhanced scalability (b) compared to its non-equivariant counterpart. PI denotes the Permutation-EquIvariant property.
对比置换等变（PI）架构与非PI基线在Small（196.49M）、Base（390.13M）、Large（892.37M）三种模型规模下的性能。

PI架构在所有规模下均表现更优，Large模型性能较基线提升45%，且收敛速度更快、样本效率更高，验证了其强可扩展性。

6.【总结展望】

6.1 总结

6.2 展望

未来可针对模型局限性进行优化，如改进对透明物体的处理能力、提升几何重建细节、减少点云生成的网格伪影；同时可探索在更多动态场景和复杂环境中的应用，进一步拓展其在增强现实、机器人导航等领域的实用价值。

7.【快速上手】

7.1 快速开始

克隆仓库并安装依赖
首先，克隆代码仓库并安装所需的依赖包。

git clone https://github.com/yyfz/Pi3.git
cd Pi3
pip install -r requirements.txt

通过命令行运行推理
可使用示例推理脚本，支持对图像目录或视频文件进行处理。

若从Hugging Face自动下载模型较慢，可手动从[此链接]下载模型检查点，并通过--ckpt参数指定本地路径。

# 使用默认示例视频运行
python example.py

# 在自定义数据上运行（图像文件夹或.mp4文件）
python example.py --data_path <你的图像目录或视频文件路径>

可选参数说明：

--data_path：输入图像目录或视频文件路径（默认：examples/skating.mp4）
--save_path：输出.ply点云的保存路径（默认：examples/result.ply）
--interval：帧采样间隔（默认：图像为1，视频为10）
--ckpt：自定义模型检查点文件路径
--device：运行推理的设备（默认：cuda）

运行Gradio交互演示
也可启动本地Gradio演示，获得交互式使用体验。

# 安装演示专用依赖
pip install -r requirements_demo.txt

# 启动演示
python demo_gradio.py

7.2 详细使用说明

模型输入与输出

模型接收图像张量作为输入，并输出包含重建几何信息的字典。

输入：形状为B×N×3×H×W的torch.Tensor，像素值范围为[0, 1]（B为批次大小，N为图像数量，H、W为图像高、宽）。
输出：包含以下键的字典
- points：通过局部点和相机姿态反投影得到的全局点云（torch.Tensor，形状B×N×H×W×3）
- local_points：每视角的局部点图（torch.Tensor，形状B×N×H×W×3）
- conf：局部点的置信度分数（值范围[0, 1]，越高越好，torch.Tensor，形状B×N×H×W×1）
- camera_poses：相机到世界的变换矩阵（OpenCV格式4×4矩阵，torch.Tensor，形状B×N×4×4）

示例代码片段

以下是在一批图像上运行模型的极简示例。

import torch
from pi3.models.pi3 import Pi3
from pi3.utils.basic import load_images_as_tensor  # 假设已存在该辅助函数

# --- 初始化设置 ---
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = Pi3.from_pretrained("yyfz233/Pi3").to(device).eval()
# 或从链接下载检查点：`https://huggingface.co/yyfz233/Pi3/resolve/main/model.safetensors`

# --- 加载数据 ---
# 将N张图像序列加载为张量
# 图像形状：(N, 3, H, W)，值范围：[0, 1]
imgs = load_images_as_tensor('你的数据路径', interval=10).to(device)

# --- 推理过程 ---
print("运行模型推理...")
# 在兼容GPU上使用混合精度以提升性能
dtype = torch.bfloat16 if (torch.cuda.is_available() and torch.cuda.get_device_capability()[0] >= 8) else torch.float16

with torch.no_grad():
    with torch.amp.autocast('cuda', dtype=dtype):
        # 添加批次维度 -> (1, N, 3, H, W)
        results = model(imgs[None])

print("重建完成！")
# 访问输出：results['points']、results['camera_poses']和results['local_points']