目标检测之—— 边框损失函数

目标检测的损失函数由两部分组成，置信损失函数，边框回归损失函数。本文记录边框回归损失函数的演变。

1. L1/L2 Loss

最开始是使用L1/L2 loss ，定义如下，其中输入x为预测值与真实值之差：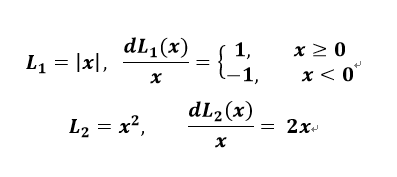

缺点：L1 Loss 对 x 的导数为常数，训练后期，x很小，反向求导更新权值时，由于x非常小，导数为常数，学习率不改变的情况下，损失函数会在一个稳定值附近波动，权值没什么变动。L2 Loss 在训练初期时，x值很大，导数也相应大，在初期训练不稳定。

2. Smooth L1 Loss

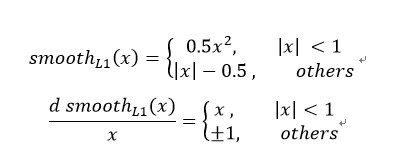
这里结合了L1 Loss和L2 Loss ,在训练初期，即x较大时，用L1 Loss；在训练后期，即x较小时，用L2 Loss.

3. IoU Loss

L1/L2 Loss ，Smooth L1Loss 默认输入的值相互独立，即对每个值求损失再相加，这与实际情况不符，针对这一情况IoU被提出：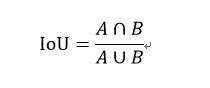

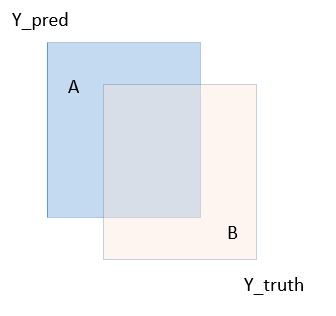
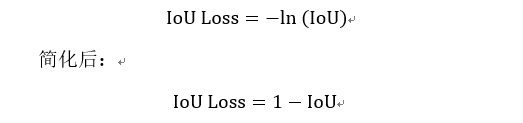
计算让输入 x,y,w,h相互关联，具备尺度不变性。克服了前面几个损失函数的缺陷。但 IoU Loss也有不足：
1，当真实框与预测框不相交时，IoU 为零，无法反映两个框的远近，也就无法学习不相交的情况。
2，当真实框与预测框相交时，IoU 一样，但他们相交情况可能不一样，如下图所示,两种情况的IoU值相同，但我们认为右边情况要好些，IoU无法反映。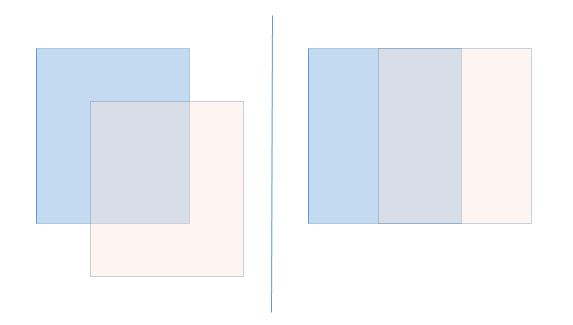

4. GIoU Loss

定义：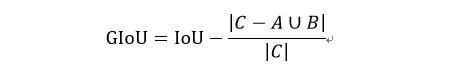

其中C 为真实框与预测框的最小外接矩形，用最小外接矩形减去两个框的交集，GIoU 取值范围为[1,-1],当两个框重合时，取最大值1，当两个框不相交时取最小值-1，当两个框相交时，GIoU不仅考虑了重叠部分，也考虑了其他非重叠部分，更好的反映了两个框的重叠情况。
缺点：当预测框完全包含于真实框时，如下图所示，我们默认左边的匹配情况好些，但此时GIoU与IoU值一样，无法学习这类情况。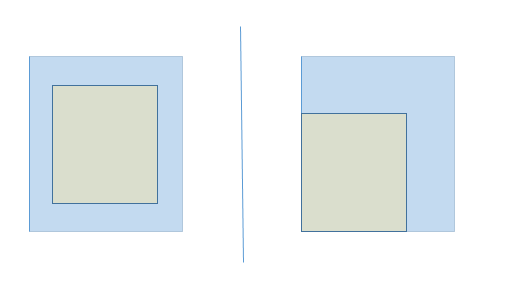

4. DIoU Loss

定义：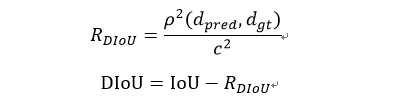

其中d_pred,d_gt分别为预测框和真实框的中心点，p为求欧氏距离，c为最小外接矩形的对角线。
缺点：边框回归三要素 重叠面积，中心点距离和长宽比，DIoU没有考虑长宽比，所以又提出 CIoU 把长宽比考虑了进去。