科普文:算法和数据结构系列【树:4叉树、N叉树】
树的定义:树是由n(n>=0)个元素节点组成的有限集合,当n=0时,称为空树。对于非空树应满足以下要求:(1)有且仅有一个根节点;(2)当n>1时,其余节点可分成m(m>=0)个互不相交的有限集合,其中每一个集合本身又是一棵树,称为根的子树。从定义中我们可以得到以下结论:1)树是分支分层结构;2)树中仅有根节点没有父节点;3)除根节点外,其余节点有且仅有一个父节点;4)树中每个节点,可以有零个或多
概叙
科普文:算法和数据结构系列【非线性数据结构:树Tree和堆Heap的原理、应用、以及java实现】-CSDN博客
科普文:算法和数据结构系列【非线性数据结构:图Graph的原理、应用、以及java实现】-CSDN博客
科普文:算法和数据结构系列【排序算法:常见10种排序算法的原理、应用、以及java实现】-CSDN博客
科普文:算法和数据结构系列【查找算法:常见7种查找算法的原理、应用、以及java实现】-CSDN博客
前面我们已经梳理了常见的数据结构、10大排序算法、7大查找算法。这里把树拿出来,再做一点补充。为啥要补充一下,主要原因是树在组织数据、表示层级关系以及提高数据操作效率方面具有独特优势,并且符合人类的学习习惯。
学习树结构对于提高数据处理效率、优化算法设计、增强问题解决能力以及符合人类学习习惯等方面都具有重要意义。特别是对递归、遍历、有序性的理解,了解完树,会理解的更深。
为了和二叉树做区分,我们这里就整两个不常见的树:4叉树、N叉树,来做示例讲解。
树的定义
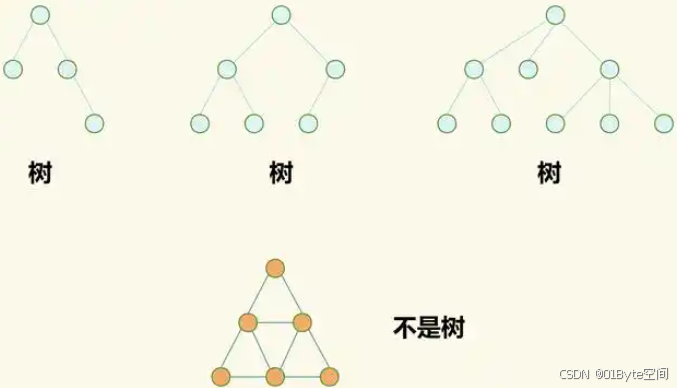
树的定义:树是由n(n>=0)个元素节点组成的有限集合,当n=0时,称为空树。
对于非空树应满足以下要求:
(1)有且仅有一个根节点;
(2)当n>1时,其余节点可分成m(m>=0)个互不相交的有限集合,其中每一个集合本身又是一棵树,称为根的子树。
从定义中我们可以得到以下结论:
1)树是分支分层结构;
2)树中仅有根节点没有父节点;
3)除根节点外,其余节点有且仅有一个父节点;
4)树中每个节点,可以有零个或多个子节点;
5)根节点到任何除自身之外的节点,有且仅有一条路径;
学习树的意义
- 首先,树结构非常适合表示自然界或信息系统中的分层结构,如家谱、公司组织架构、文件目录等。其根节点表示起点或最高层级,子节点逐级代表下层关系,这种层次性使得树结构在组织和表示复杂关系时非常直观和高效。
- 其次,树结构在数据查找和更新方面具有显著优势。在大量数据的组织和查询中,线性结构(如数组、链表)需要遍历所有元素,时间复杂度较高,通常是O(n)。而树的层级结构,特别是平衡树,可以在O(log n)或O(h)时间内完成查找、插入、删除等操作(其中h为树的高度),大大提高了数据操作的效率。
- 此外,树结构还符合人类的学习习惯和分类归纳的本能。树状结构就像树木一样,有主干、分支、枝叶,可以层层细分,帮助我们看清主次内容,理清思路逻辑。通过树状结构,我们可以更好地分类归纳知识,发现规律,深化认知。
- 最后,树结构在计算机科学中有着广泛的应用,如数据库索引、网络路由、AI搜索等领域。掌握树结构有助于我们更好地理解和解决这些领域中的实际问题。
学习树的作用
学习树结构具有非常实际的用处。学习树结构不仅有助于我们更好地理解和组织知识,还能在提高数据操作效率、解决实际问题以及符合人类认知习惯等方面发挥重要作用。
以下是几个核心的应用场景和优势:
-
知识整理与结构化:在学习知识或做笔记时,树结构能够清晰地展示知识的层次和关系。例如,整理历史朝代的发展脉络,可以将朝代作为树干,政治、经济、文化等作为大分枝,进一步细化为小分枝,形成一目了然的知识体系。树形图或思维导图等树结构工具,有助于全面理解知识结构,快速掌握原理和思维方法,找到事物间的内在联系。
-
高效的数据操作:在数据结构中,树结构如平衡树(红黑树、AVL树等)能够保持相对平衡,使得查找、插入和删除操作的时间复杂度为O(log n),远高于数组的O(n)复杂度,提高了数据操作的效率。树结构支持快速的动态操作,特别适合频繁的动态插入和删除场景,同时提供高效的查询性能。
-
广泛的应用领域:树结构在图书管理、文件系统、组织架构、族谱管理等领域有广泛应用,能够高效地对数据进行分类分层管理。在计算机科学中,树结构是数据库索引(如B树、B+树)、网络路由、AI搜索等领域的基础数据结构,对于提高系统性能和优化算法设计具有重要意义。
-
符合人类认知习惯:树形层级结构是人类认知、思考、分析的主要结构,具有简洁、清晰、高效的特点。它符合人类分类、归纳、理解的本能,有助于我们更好地组织和记忆信息。
树的抽象定义
树的基类:
/**
* @author zhouxx
* @create 2025-01-11 14:49
*/
public class BaseTreeNode<T extends Comparable<T>> {
T value;
public BaseTreeNode(){
this(null);
}
public BaseTreeNode(T value){
this.value=value;
}
}树的接口:
/**
* @author zhouxx
* @create 2025-01-10 12:48
*/
public interface Tree<T extends Comparable<T>> {
// 抽象方法,具体实现由子类提供
public void buildTree(T[] array);
public void add(T value);
public void remove(T value);
public void find(T value);
/**
* 遍历
*
* 深度优先遍历(Depth First Search, DFS):深度优先遍历是一个递归的过程,从树的根节点开始,沿着树的深度方向一直遍历到叶节点,然后回溯到父节点,再继续遍历其他未访问的子节点。
* 深度优先遍历有三种具体的遍历方式:
* 前序遍历(先访问根节点,再访问左子树,最后访问右子树)、
* 中序遍历(先访问左子树,再访问根节点,最后访问右子树)
* 后序遍历(先访问左子树,再访问右子树,最后访问根节点)。
*
* 广度优先遍历(Breadth First Search, BFS):广度优先遍历是一种逐层访问节点的遍历方式(层次遍历),从树的根节点开始,先访问所有相邻的节点(即同一层的节点),然后再逐层向下访问相邻的节点。
*
* */
// 前序遍历(先访问根节点,再访问左子树,最后访问右子树)
public void preOrder();
// 中序遍历(先访问左子树,再访问根节点,最后访问右子树)
public void inOrder();
// 后序遍历(先访问左子树,再访问右子树,最后访问根节点)
public void postOrder();
// 层序遍历:根节点开始,逐层访问节点的遍历方式(层次遍历)
public void levelOrder();
}四叉树
四叉树的节点定义
/**
* @author zhouxx
* @create 2025-01-10 11:17
*/
public class _4TreeNode<T extends Comparable<T>> {
T value;
_4TreeNode<T> parentNode;
_4TreeNode<T> leftNode; /**二叉树是最多只有左右两个子节点*/
_4TreeNode<T> rightNode;
_4TreeNode<T> leftNode1;//非二叉树
_4TreeNode<T> rightNode1;//非二叉树
public _4TreeNode(T value) {
this.value = value;
this.parentNode=null;
this.leftNode=null;
this.rightNode=null;
this.leftNode1=null;
this.rightNode1=null;
}
//是否是叶子节点
public boolean isLeaf(){
return (this.leftNode==null && this.rightNode==null&& this.leftNode1==null&& this.rightNode1==null);
}
//是否是叶子节点
public boolean isRoot(){
return (this.parentNode==null);
}
@Override
public String toString() {
StringBuilder stringBuilder=new StringBuilder("{");
stringBuilder.append("value=").append(value).append(",");
stringBuilder.append("isLeaf=").append(isLeaf()).append(",");
stringBuilder.append("isRoot=").append(isRoot()).append(",");
stringBuilder.append("parentNode=").append(parentNode==null?"":parentNode.value).append(",");
stringBuilder.append("leftNode=").append(leftNode==null?"":leftNode.value).append(",");
stringBuilder.append("rightNode=").append(rightNode==null?"":rightNode.value).append(",");
stringBuilder.append("leftNode1=").append(leftNode1==null?"":leftNode1.value).append(",");
stringBuilder.append("rightNode1=").append(rightNode1==null?"":rightNode1.value).append(",");
stringBuilder.append("}");
return stringBuilder.toString();
//return value.toString();
}
}四叉树
package com.zxx.study.algorithm.datastruct.DataStructures.mtree.tree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
/**
* @author zhouxx
* @create 2025-01-10 16:18
*/
public class _4ChildTree<T extends Comparable<T>> implements Tree<T> {
_4TreeNode<T> root;
int cnt;
public _4ChildTree() {
root = null;
}
//遍历打印
public void printTree( _4TreeNode<T> node) {
if (node == null) {
//cnt=0;
return;
}
cnt++;
System.out.println(cnt + "打印:" + node.toString() + " ");
if (node.leftNode != null) {
printTree(node.leftNode);
}
if (node.rightNode != null) {
printTree(node.rightNode);
}
if (node.leftNode1 != null) {
printTree(node.leftNode1);
}
if (node.rightNode1 != null) {
printTree(node.rightNode1);
}
}
@Override
public void buildTree(T[] array) {
for (T tmp : array) {
add(tmp);
// cnt=0;
// System.out.println("==="+tmp);
// printTree(root);
}
}
@Override
public void add(T data) {
_4TreeNode<T> newNode = new _4TreeNode<>(data);
//维护root
if (root == null) {
root = newNode;
return;
}
//维护下一层
add(root, newNode);
}
public void add(_4TreeNode<T> current, _4TreeNode<T> newNode) {
if (current != null ) {
// 每次维护一层
if (current.leftNode == null && newNode.parentNode == null) {
newNode.parentNode = current;
current.leftNode = newNode;
return;
}
if (current.rightNode == null&& newNode.parentNode == null) {
newNode.parentNode = current;
current.rightNode = newNode;
return;
}
if (current.leftNode1 == null&& newNode.parentNode == null) {
newNode.parentNode = current;
current.leftNode1 = newNode;
return;
}
if (current.rightNode1 == null&& newNode.parentNode == null) {
newNode.parentNode = current;
current.rightNode1 = newNode;
return;
}
//父节点为空,说明上一层已经挂满了
if (newNode.parentNode == null) {
// 维护下一层
add(current.leftNode, newNode);
add(current.rightNode, newNode);
add(current.leftNode1, newNode);
add(current.rightNode1, newNode);
}
}
}
@Override
public void remove(T data) {
// 叶子节点,直接删除
//非叶子节点,其子节点要处理
// 采用广度优先,逐层遍历
}
//遍历搜索
//todo 因为是无序,所以查找必须遍历所有节点
public void search( _4TreeNode<T> node,T data,List<_4TreeNode<T>> result ) {
if (node == null) {
//cnt=0;
return;
}
if(node.value.compareTo(data)==0){
result.add(node);
}
if (node.leftNode != null) {
search(node.leftNode,data,result);
}
if (node.rightNode != null) {
search(node.rightNode,data,result);
}
if (node.leftNode1 != null) {
search(node.leftNode1,data,result);
}
if (node.rightNode1 != null) {
search(node.rightNode1,data,result);
}
}
@Override
public void find(T data) {
search(data);
}
public List<_4TreeNode<T>> search(T data) {
List<_4TreeNode<T>> result = new ArrayList<>();
search(root,data,result);
return result;
}
// 前序遍历(先访问根节点,再访问左子树,最后访问右子树) todo 四叉树姑且按照二叉树的来遍历
public void preOrder(_4TreeNode<T> node) {
if (node == null) {return;}
System.out.println( node.value); // 访问当前节点
preOrder(node.leftNode);
preOrder(node.rightNode);
preOrder(node.leftNode1);
preOrder(node.rightNode1);
}
public void inOrder(_4TreeNode<T> node) {
if (node == null) {return;}
preOrder(node.leftNode);
System.out.println( node.value); // 访问当前节点
preOrder(node.rightNode);
preOrder(node.leftNode1);
preOrder(node.rightNode1);
}
public void postOrder(_4TreeNode<T> node) {
if (node == null) {return;}
preOrder(node.leftNode);
preOrder(node.rightNode);
System.out.println( node.value); // 访问当前节点
preOrder(node.leftNode1);
preOrder(node.rightNode1);
}
public void levelOrder(_4TreeNode<T> node) {
if (node == null) {return;}
Queue<_4TreeNode<T>> queue = new LinkedList<>();
queue.offer(node);
while (!queue.isEmpty()) {
//首先将根节点入队,然后在循环中不断地从队列中取出节点、打印节点的值,并将该节点的所有子节点入队。
// 这样就能够按照层级顺序遍历整个树。
_4TreeNode<T> currentNode = queue.poll();
System.out.println( currentNode.value); // 访问当前节点
if (currentNode.leftNode != null) {queue.offer(currentNode.leftNode);}
if (currentNode.rightNode != null) {queue.offer(currentNode.rightNode);}
if (currentNode.leftNode1 != null) {queue.offer(currentNode.leftNode1);}
if (currentNode.rightNode1 != null) {queue.offer(currentNode.rightNode1);}
}
}
@Override
public void preOrder() {
preOrder(root);
}
@Override
public void inOrder() {
inOrder(root);
}
@Override
public void postOrder() {
postOrder(root);
}
@Override
public void levelOrder() {
levelOrder(root);
}
}
测试验证:
/**
* @author zhouxx
* @create 2025-01-10 18:19
*/
public class TestTree {
public static void main(String[] args) {
_4ChildTree<Integer> a4ChildTree =new _4ChildTree<>();
Integer[] array=null;
List<_4TreeNode<Integer>> result=null;
array=new Integer[]{2,2,2,2,2,2,2,2,2};
a4ChildTree.buildTree(array);
a4ChildTree.printTree(a4ChildTree.root);//打印
result=a4ChildTree.search(2);
System.out.println(array.length+","+result.size()+" , "+result.toString());
Integer[] array1={1,2,3,4,5,6,7,8,9,10};
a4ChildTree =new _4ChildTree<>();
a4ChildTree.buildTree(array1);
a4ChildTree.printTree(a4ChildTree.root);//打印
for(int data:array1) {
result = a4ChildTree.search(data);
System.out.println(array1.length + "," + result.size() + " , " + result.toString());
}
}
}运行结果
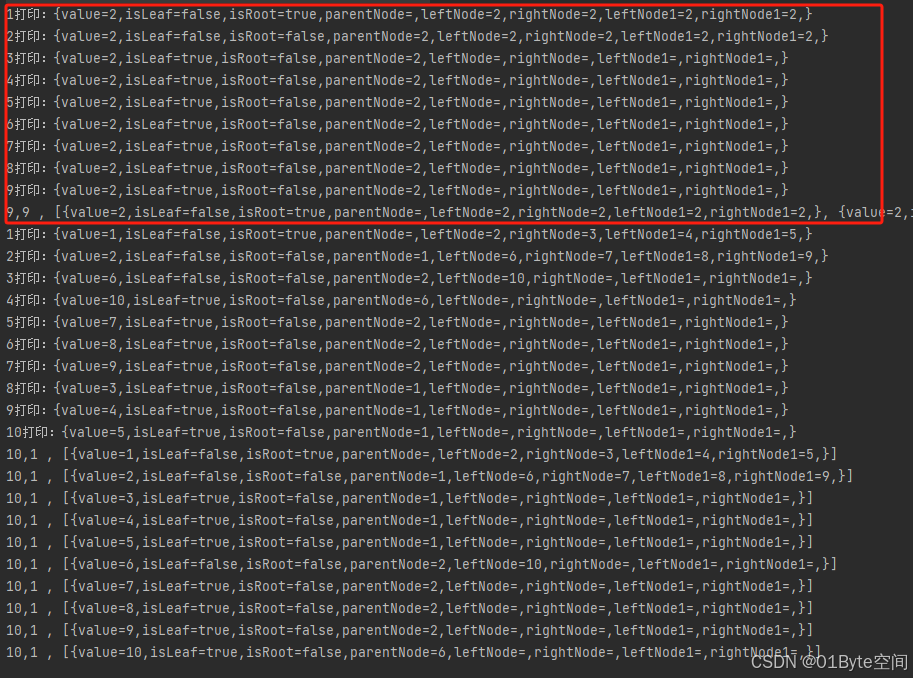
示例一:在四叉树中插入了9个值为2的节点,搜索值为2的节点,打印搜索结果(刚好是9个值为2的节点),符合预期,四叉树结果无误。
示例二:在四叉树中插入1-10不重复的10个数,观察其结果,逐个搜索验证其搜索方法。
可以看到四叉树刚好是4层
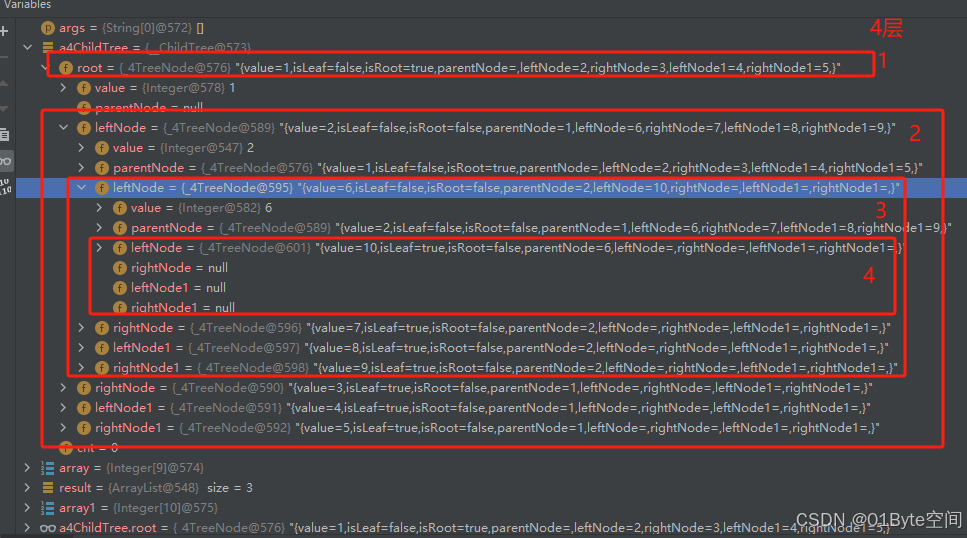
符合预期
N叉树
N茶树的节点定义
import java.util.ArrayList;
import java.util.List;
/**
* @author zhouxx
* @create 2025-01-11 13:37
*/
public class _NaryTreeNode<T extends Comparable<T>> extends BaseTreeNode {
List<_NaryTreeNode<T>> children;
// 构造方法
public _NaryTreeNode(T value) {
super(value);
this.value = value;
this.children = new ArrayList<>();
}
// 添加子节点的方法
public void addChild(_NaryTreeNode<T> child) {
children.add(child);
}
}
N叉树
package com.zxx.study.algorithm.datastruct.DataStructures.mtree.tree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
/**
* @author zhouxx
* @create 2025-01-11 13:38
*/
public class _NaryTree<T extends Comparable<T>> implements Tree<T> {
_NaryTreeNode root;
public _NaryTree() {
this(null);
}
// 构造方法
public _NaryTree(T value) {
this.root = new _NaryTreeNode(value);
}
@Override
public void buildTree(T[] array) {
if (array == null || array.length == 0) {
return;
}
// 假设数组的第一个元素是根节点的值
this.root = new _NaryTreeNode<T>(array[0]);
// 使用一个队列来按层次构建树
Queue<_NaryTreeNode<T>> queue = new LinkedList<>();
queue.offer(this.root);
int index = 1;
while (!queue.isEmpty() && index < array.length) {
_NaryTreeNode<T> currentNode = queue.poll();
// 为当前节点添加子节点
while (index < array.length && canAddChild(currentNode, array[index])) {
_NaryTreeNode<T> child = new _NaryTreeNode<>(array[index]);
currentNode.addChild(child);
queue.offer(child);
index++;
}
}
}
// 辅助方法:判断是否可以将给定值作为当前节点的子节点
// 这里可以根据具体需求来实现,比如限制子节点的数量或根据值的某种特性来决定
private boolean canAddChild(_NaryTreeNode<T> parentNode, T childValue) {
// 简单的实现:总是可以添加子节点
return true;
}
@Override
public void add(T data) {
if (this.root == null) {
this.root = new _NaryTreeNode<T>(data);
} else {
_NaryTreeNode<T> newNode = new _NaryTreeNode<>(data);
this.root.addChild(newNode);
}
}
@Override
public void remove(T value) {
boolean deleted = deleteRecursively(root,value);
if (deleted) {
System.out.println("Node with value "+value.toString()+" was deleted.");
} else {
System.out.println("Node with value "+value.toString()+" was not found or could not be deleted.");
}
}
// 递归删除方法
private boolean deleteRecursively(_NaryTreeNode<T> currentNode, T value) {
if (currentNode == null) {
return true;
}
// 如果当前节点的值就是要删除的值
if (currentNode.value.compareTo(value)==0) {
// 如果当前节点是叶子节点,直接返回true表示可以删除
// 如果在子树中成功删除了节点,则从当前节点的子节点列表中移除该子节点
currentNode.value=null;
currentNode.children=null;
// 如果当前节点不是叶子节点,则需要将其子节点全部“提升”到当前节点的父节点下
// 这里为了简化,我们不实现子节点的提升,而是简单地返回false表示不能删除非叶子节点
// 在实际应用中,你可能需要实现更复杂的逻辑来处理这种情况
return true;
}
// 遍历子节点进行递归删除
for (_NaryTreeNode<T> child : currentNode.children) {
if (!deleteRecursively(child, value)) {
// 可以根据需要返回true或继续检查其他子节点
// 这里我们假设只要删除了一个节点就返回true
return false;
}
}
// 没有在子节点中找到要删除的值
return true;
}
public List<_NaryTreeNode<T>> search(T data) {
List<_NaryTreeNode<T>> result=new ArrayList<>();
search(root,data,result);
return result;
}
public void search(_NaryTreeNode<T> node,T data,List<_NaryTreeNode<T>> result) {
if (node != null) {
if(node.value.compareTo(data)==0) {
result.add(node);
}
for (_NaryTreeNode<T> child : node.children) {
search(child,data,result); // 递归地访问每个子节点
}
}
}
@Override
public void find(T data) {
search(data);
}
@Override
public void preOrder() {
preOrder(root);
}
@Override
public void inOrder() {
inOrder(root);
}
@Override
public void postOrder() {
postOrder(root);
}
@Override
public void levelOrder() {
levelOrder(root);
}
public void preOrder(_NaryTreeNode<T> node) {
if (node != null) {
System.out.println( node.value); // 访问当前节点
for (_NaryTreeNode<T> child : node.children) {
preOrder(child); // 递归地访问每个子节点
}
}
}
//中序遍历(对于N叉树来说,中序遍历的定义可能不太直观,但我们可以理解为先遍历第一个子树,然后访问根节点,最后遍历剩余的子树)
public void inOrder(_NaryTreeNode<T> node) {
if (node != null) {
// 先遍历第一个子节点
if (!node.children.isEmpty()) {
inOrder(node.children.get(0));
}
// 然后访问当前节点
System.out.println(node.value);
// 最后遍历剩余的子节点
for (int i = 1; i < node.children.size(); i++) {
inOrder(node.children.get(i));
}
}
}
//后序遍历(先遍历所有子节点,然后访问根节点)
public void postOrder(_NaryTreeNode<T> node) {
if (node != null) {
// 先遍历所有子节点
for (_NaryTreeNode<T> child : node.children) {
postOrder(child);
}
// 然后访问当前节点
System.out.println(node.value);
}
}
//层次遍历(按层级从上到下、从左到右遍历节点)
//层次遍历通常使用队列来实现,因为它需要按照层级顺序访问节点。
public void levelOrder(_NaryTreeNode<T> node) {
if (node == null) {
return;
}
//队列来保存待访问的节点
Queue<_NaryTreeNode<T>> queue = new LinkedList<>();
queue.offer(node);
while (!queue.isEmpty()) {
//首先将根节点入队,然后在循环中不断地从队列中取出节点、打印节点的值,并将该节点的所有子节点入队。
// 这样就能够按照层级顺序遍历整个树。
_NaryTreeNode<T> currentNode = queue.poll();
System.out.println(currentNode.value);
for (_NaryTreeNode<T> child : currentNode.children) {
//队列来保存待访问的节点
queue.offer(child);
}
}
}
// 辅助方法:打印树的结构(参考前序遍历)
public void printTree(_NaryTreeNode<T> node, String prefix) {
if (node != null) {
System.out.println(prefix + node.value);
if(node.children!=null) {
for (_NaryTreeNode<T> child : node.children) {
printTree(child, prefix + "--");
}
}
}
}
}
测试验证
/**
* @author zhouxx
* @create 2025-01-11 13:46
*/
public class _NaryTreeTest {
public static void main(String[] args) {
_NaryTree<Integer> tree = new _NaryTree(1);
_NaryTreeNode<Integer> node2 = new _NaryTreeNode(2);
_NaryTreeNode<Integer> node3 = new _NaryTreeNode(3);
_NaryTreeNode<Integer> node4 = new _NaryTreeNode(4);
_NaryTreeNode<Integer> node5 = new _NaryTreeNode(5);
_NaryTreeNode<Integer> node6 = new _NaryTreeNode(6);
_NaryTreeNode<Integer> node7 = new _NaryTreeNode(7);
tree.root.addChild(node2);
tree.root.addChild(node3);
node2.addChild(node4);
node2.addChild(node5);
node2.addChild(node6);
node6.addChild(node7);
System.out.println("Before deletion:");
tree.printTree(tree.root, "");
tree.remove(2);
System.out.println("After deletion:");
tree.printTree(tree.root, "");
Integer[] array1={1,2,3,4,5,6,7,8,9,10};
_NaryTree<Integer> tree2 = new _NaryTree();
tree2.buildTree(array1);
tree2.printTree(tree2.root, "-");
tree2.root.children.add(new _NaryTreeNode(11));
_NaryTreeNode<Integer> tmpNode= (_NaryTreeNode<Integer>) tree2.root.children.get(2);
tmpNode.children.add(new _NaryTreeNode(12));
tree2.root.children.add(tmpNode);
_NaryTreeNode<Integer> node71 = new _NaryTreeNode(71);
node71.addChild(tmpNode);
tree2.root.children.add(node71);
tree2.printTree(tree2.root, "-");
tree2.root.addChild(node71);
tree2.printTree(tree2.root, "-");
}
}
找到值的节点,将其整个删除
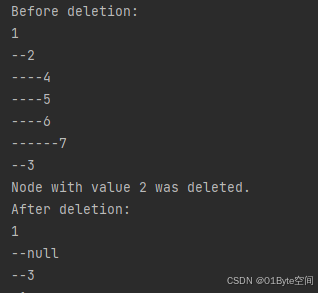
N叉树添加节点
Before deletion:
1
--2
----4
----5
----6
------7
--3
Node with value 2 was deleted.
After deletion:
1
--null
--3
-1
---2
---3
---4
---5
---6
---7
---8
---9
---10
-1
---2
---3
---4
-----12
---5
---6
---7
---8
---9
---10
---11
---4
-----12
---71
-----4
-------12
-1
---2
---3
---4
-----12
---5
---6
---7
---8
---9
---10
---11
---4
-----12
---71
-----4
-------12
---71
-----4
-------12
Process finished with exit code 0
至此4叉树和N叉树都已经讲解完毕,重点是方法中的注解,可以帮助更好的理解数这个数据结构和其操作。不足的地方,欢迎留言交流指正。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容





所有评论(0)