深度学习 – 梯度计算及上下文控制

---

一，自动微分

自动微分模块torch.autograd负责自动计算张量操作的梯度，具有自动求导功能。自动微分模块是构成神经网络训练的必要模块，可以实现网络权重参数的更新，使得反向传播算法的实现变得简单而高效。

1.1 基础概念

1. 张量

   Torch中一切皆为张量，属性requires_grad决定是否对其进行梯度计算。默认是 False，如需计算梯度则设置为True。

2. 计算图：

   torch.autograd通过创建一个动态计算图来跟踪张量的操作，每个张量是计算图中的一个节点，节点之间的操作构成图的边。

   在 PyTorch 中，当张量的 requires_grad=True 时，PyTorch 会自动跟踪与该张量相关的所有操作，并构建计算图。每个操作都会生成一个新的张量，并记录其依赖关系。当设置为 True 时，表示该张量在计算图中需要参与梯度计算，即在反向传播（Backpropagation）过程中会自动计算其梯度；当设置为 False 时，不会计算梯度。

• 计算依赖图
  
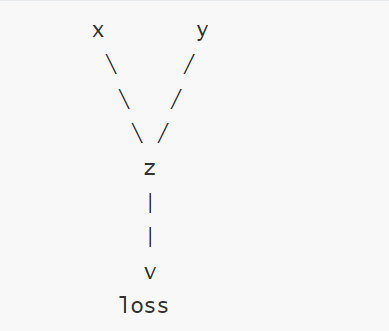
  叶子结点判断方式

x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)  # 叶子节点
y = x ** 2  # 非叶子节点（通过计算生成）
z = y.sum()

print(x.is_leaf)  # True
print(y.is_leaf)  # False
print(z.is_leaf)  # False

1.2 计算梯度

使用tensor.backward()方法执行反向传播，从而计算张量的梯度

1.2.1 计算标量梯度

import torch

def test01():
    x= torch.tensor(1.0,requires_grad=True)# requires_grad=True表示需要求导

    y=x**2# 操作张量

    y.backward() #计算梯度，也就是反向传播

    print(x.grad) # 打印梯度

if __name__ == '__main__':
    test01()

1.2.2 计算向量梯度

def test002():
    # 1. 创建张量：必须为浮点类型
    x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
    y = x ** 2
    loss = y.mean()
    loss.backward()
    print(x.grad)


if __name__ == "__main__":
    test002()

调用 loss.backward() 从输出节点 loss 开始，沿着计算图反向传播，计算每个节点的梯度。

损失函数$$loss=mean(y)=\frac{1}{n}\sum _{i=1}^n{y}_i$$，其中 n=3。

对于每个 $y_i$，其梯度为 $\frac{\partial loss}{\partial y_i}=\frac{1}{n}=\frac{1}{3}$。

对于每个 $x_i$，其梯度为：
$$\frac{\partial loss}{\partial x_i}=\frac{\partial loss}{\partial y_i}\times \frac{\partial y_i}{\partial x_i}=\frac{1}{3}\times 2x_i=\frac{2x_i}{3}$$
所以，x.grad 的值为：$[\frac{2\times 1.0}{3},\frac{2\times 2.0}{3},\frac{2\times 3.0}{3}]=[\frac{2}{3},\frac{4}{3},2]\approx [0.6667,1.3333,2.0000]$

1.2.3 多标量梯度计算

#多标量梯度计算
def test03():
    x1= torch.tensor(1.0,requires_grad=True)
    x2=torch.tensor(3.0,requires_grad=True)

    y=x1**2+x2*7
    z=y.sum()
    z.backward()
    print(x1.grad,x2.grad)

if __name__ == '__main__':
    test03()

1.2.4 多向量梯度计算

# 多向量梯度计算
def test04():
    x1 = torch.tensor([1.0, 2.0], requires_grad=True)
    x2 = torch.tensor([3.0, 4.0], requires_grad=True)

    y = x1 ** 2 + x2 * 7
    z = y.sum()
    z.backward()
    print(x1.grad, x2.grad)

if __name__ == '__main__':
    test04()

二，梯度上下文控制

梯度计算的上下文控制和设置对于管理计算图、内存消耗、以及计算效率至关重要。下面我们学习下Torch中与梯度计算相关的一些主要设置方式。

2.1 控制梯度计算

简单的运算不需要梯度

import torch

def test01():
    x=torch.tensor(11.5,requires_grad=True)
    print(x.requires_grad)# True

    y=x**2
    print(y.requires_grad)# True

    with torch.no_grad():
        z=x**2
    print(z.requires_grad)

    #使用装饰器
    @torch.no_grad()
    def test():
        return x**2
    y=test()
    print(y.requires_grad)
    



if __name__ == '__main__':
    test01()

2.2 累计梯度

默认情况下，当我们重复对一个自变量进行梯度计算时，梯度是累加的

import torch


def test002():
    x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)

    # 2. 累计梯度：每次计算都会累计梯度
    for i in range(3):
        y = x**2 + 2 * x + 7
        z = y.mean()
        z.backward()
        print(x.grad)


if __name__ == "__main__":
    test002()

2.3 梯度清零

大多数情况下是不需要梯度累加的

#梯度清零
def test002():
    x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)

    # 2. 累计梯度：每次计算都会累计梯度
    for i in range(3):
        y = x**2 + 2 * x + 7
        z = y.mean()
        # 2.1 反向传播之前先对梯度进行清零
        if x.grad is not None:
            x.grad.zero_()
            
        z.backward()
        print(x.grad)


if __name__ == "__main__":
    test002()

三，案例一----求函数最小值

import torch
from matplotlib import pyplot as plt
import numpy as np


def test01():
    x = np.linspace(-10, 10, 100)
    y = x ** 2

    plt.plot(x, y)

    plt.show()


def test02():
    # 初始化自变量X
    x = torch.tensor([3.0], requires_grad=True, dtype=torch.float)
    # 迭代轮次
    epochs = 50
    # 学习率
    lr = 0.1

    list = []
    for i in range(epochs):
        # 计算函数表达式
        y = x ** 2

        # 梯度清零
        if x.grad is not None:
            x.grad.zero_()
        # 反向传播
        y.backward()
        with torch.no_grad():
            x -= lr * x.grad

        print('epoch:', i, 'x:', x.item(), 'y:', y.item())
        list.append((x.item(), y.item()))

    # 散点图，观察收敛效果
    x_list = [l[0] for l in list]
    y_list = [l[1] for l in list]

    plt.scatter(x=x_list, y=y_list)
    plt.show()


if __name__ == "__main__":
    test01()
    test02()

四，案例二----函数参数求解

import torch

def test02():
    x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)
    y = torch.tensor([3, 5, 7, 9, 11], dtype=torch.float)

    a = torch.tensor([1.0], dtype=torch.float, requires_grad=True)
    b = torch.tensor([1.0], dtype=torch.float, requires_grad=True)

    lr = 0.05
    epochs = 1000

    for epoch in range(epochs):
        y_pred = a * x + b
        loss = ((y_pred - y) ** 2).mean()

        if a.grad is not None:
            a.grad.zero_()
        if b.grad is not None:
            b.grad.zero_()

        loss.backward()

        with torch.no_grad():
            a -= lr * a.grad
            b -= lr * b.grad

        if (epoch + 1) % 100 == 0:
            print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

    print(f'a: {a.item():.4f}, b: {b.item():.4f}')

if __name__ == '__main__':
    test02()