深度学习相关概念整理
残差连接(Residual Connection)是一种在深度学习领域,特别是在深度神经网络架构设计中的关键技术。它最初由何凯明等人在2015年的论文《Deep Residual Learning for Image Recognition》中提出,并应用于ResNet(Residual Network)中,极大地推动了深度神经网络的发展,尤其是在图像识别任务上的突破。残差连接的核心思想是引入“捷
一、残差连接是什么?
残差连接(Residual Connection)是一种在深度学习领域,特别是在深度神经网络架构设计中的关键技术。它最初由何凯明等人在2015年的论文《Deep Residual Learning for Image Recognition》中提出,并应用于ResNet(Residual Network)中,极大地推动了深度神经网络的发展,尤其是在图像识别任务上的突破。
残差连接的核心思想是引入“捷径”或“跳过连接”,它允许输入信号可以直接传递到网络的较深层,而不仅仅依赖于逐层前向传播的计算结果。具体实现上,某个层的输入不仅经过一系列的非线性变换(如卷积、ReLU激活等),其原始输入还会绕过这一系列变换,然后与变换后的输出相加。数学上可以表示为 H(x) = F(x, W) + x,其中 x 是输入,F(x, W)是包含一组可学习参数W的一系列层的组合,H(x)是最终输出,即网络要学习的是残差映射而不是原始的全映射。
这种结构有助于解决随着网络加深带来的梯度消失问题。因为在反向传播过程中,梯度可以通过捷径直接回传到浅层,无需经过所有层级的非线性激活函数的连续链式法则,从而缓解梯度消失或梯度爆炸的风险,使得优化更加稳定,进而允许构建和训练出更深层次的神经网络。此外,残差连接还有助于特征重用,增强浅层特征在网络较深层级的重要性,从而提升模型的学习能力和泛化能力。
二、MLP是什么?
多层感知机(Multilayer Perceptron, MLP): 在机器学习和人工智能领域,MLP是指一种前馈型神经网络,它是人工神经网络(Artificial Neural Network, ANN)的一种常见形式。MLP至少包含一个隐藏层,除了输入层和输出层外,还可以有多层非线性处理单元,这些单元之间采用全连接的方式。通过反向传播算法进行训练,MLP能够用于分类和回归等多种预测任务,因其具有良好的非线性建模能力而在许多领域中广泛应用。
三、前馈型神经网络和循环神经网络
前馈型神经网络(Feedforward Neural Networks, FNNs)和循环神经网络(Recurrent Neural Networks, RNNs)是两种不同类型的神经网络结构,它们在设计、用途和处理数据的方式上有显著区别:
前馈神经网络(FFNNs)
-
结构:前馈神经网络具有严格的层次结构,信息从输入层开始,通过一系列隐藏层处理,并在输出层得出最终结果。每一层的神经元只与下一层神经元连接,不存在任何反馈回路或循环路径,故称为“前馈”。
-
数据处理:这类网络主要用于处理固定长度的输入,并一次性计算输出。它不保留历史信息,每个神经元的输出只取决于当前时刻的输入值。
-
应用:前馈神经网络常用于图像识别、语音识别、自然语言处理中的分类和回归任务等,尤其擅长处理空间或时间上不具顺序依赖性的数据。
循环神经网络(RNNs)
-
结构:循环神经网络的独特之处在于它们具有时间维度上的循环连接,允许信息在网络中循环流动,让神经元不仅可以接受当前时刻的输入,还能考虑之前时刻的信息。换句话说,每个神经元的输出不仅取决于当前时刻的输入,还取决于其在前一时刻的隐藏状态。
-
数据处理:RNN非常适合处理序列数据,如文本、音频或视频序列,因为它们有能力捕获时间序列中的长期依赖关系。每一个时间步长的输出都会作为下一个时间步长的输入的一部分。
-
应用:循环神经网络广泛应用于自然语言处理(如文本生成、翻译、情感分析)、语音识别、机器翻译、音乐生成等领域,以及其他任何需要考虑时间序列上下文的任务。
总结起来,前馈神经网络是一种无记忆的、单向传播信息的网络结构,而循环神经网络则具有内在的记忆机制,能够处理和学习序列数据中的动态变化和模式。
四、RNN的早期结构和encoder-decoder架构
在深度学习时代早期,人们使用RNN(循环神经网络)来处理机器翻译任务。一段输入先是会被预处理成一个token序列。RNN会对每个token逐个做计算,并维护一个表示整段文字整体信息的状态。根据当前时刻的状态,RNN可以输出当前时刻的一个token。

这种简单的RNN架构仅适用于输入和输出等长的任务。然而,大多数情况下,机器翻译的输出和输入都不是等长的。因此,人们使用了一种新的架构。前半部分的RNN只有输入,后半部分的RNN只有输出(上一轮的输出会当作下一轮的输入以补充信息)。两个部分通过一个状态
来传递信息。把该状态看成输入信息的一种编码的话,前半部分可以叫做“编码器”,后半部分可以叫做“解码器”。这种架构因而被称为“编码器-解码器”架构。

五、注意力机制
1、自注意力机制(Self-Attention Mechanism)
一种在自然语言处理中常用的技术,主要用于捕捉输入序列内部元素之间的关系。与传统的注意力机制不同,自注意力机制不需要依赖外部目标(Target),而是在输入序列内部进行计算。
在传统的循环神经网络(RNN)或长短期记忆网络(LSTM)中,隐藏状态只能依赖于前一时刻的状态和当前时刻的输入,而自注意力机制克服了这种局限性,它让序列中的每个元素都有机会直接参考序列内的所有其他元素。
自注意力机制的核心思想是计算输入序列中每个元素与其他元素之间的关联程度,进而对输入序列进行加权表示。这种机制可以帮助模型捕捉到长距离依赖关系,从而更好地理解输入序列的结构和语义信息。
自注意力的基本工作原理包括以下几个步骤:
- 将输入序列通过不同的线性变换分别映射成三个向量:查询(Query)、键(Key)和值(Value)。
- 计算Query与Key的点积或相关度得分,经过softmax函数归一化后得到每个位置对其他所有位置的注意力权重。
- 使用得到的注意力权重对Value向量进行加权求和,生成每个位置的新向量,即自注意力上下文向量。
通过这种方式,Transformer可以自动地学习到输入序列之间的依赖关系,并且不需要像RNN那样递归地更新状态。此外,Transformer还引入了多头注意力机制,即将输入序列分为多个子序列,分别计算注意力权重,并将结果合并起来,进一步提高了模型的表达能力。
2、多头注意力机制(Multi-Head Attention Mechanism)
多头注意力机制(Multi-Head Attention)是一种在Transformer架构中被提出的创新设计,它极大地提升了处理序列数据(如自然语言)时的模型性能和效率。下面是对多头注意力机制的详细解释:
多头注意力是对自注意力机制的一个扩展和改进,它不是只执行一次注意力运算,而是并行地执行多次独立的注意力运算,每一个被称为一个“头”(head)。每个头都具有自己的Query、Key和Value投影矩阵,因此它们可以从不同的子空间角度关注输入序列的不同方面。
这种方法在Transformer架构中被广泛采用,并在多项自然语言处理任务如机器翻译、文本分类、问答系统等方面取得了显著成果。
步骤:
- 投影映射:原始的Query、Key和Value首先通过不同的线性变换矩阵,生成多个子空间的版本,比如如果设置有ℎh个头,那么对于每个输入位置都会得到ℎh组Q、K、V向量。
- 并行计算:在每个注意力头上独立地执行自注意力计算。每个头都会基于各自的Query和Key计算注意力得分,然后使用softmax函数得到归一化的注意力权重,接着用这些权重去加权对应的Value向量。
- 汇总输出:各个头计算出的注意力输出(加权后的Value向量)会被拼接在一起,然后再次通过一个线性层(也称为合并层或输出层)来整合这些信息,生成最终的注意力输出向量。
优势:
- 多样性和丰富性:多头注意力允许模型从不同的角度和特征子集上审视输入序列,因此能够捕捉到更为复杂和多元的依赖关系。
- 并行计算:由于每个头的注意力计算相互独立,可以有效地利用现代计算设备的并行计算能力,提升计算效率。
- 更好的表征学习:通过结合不同头部学到的信息,模型能构建更为全面且具有层次感的上下文表征。
六、激活函数
激活函数作用和重要性
激活函数是神经元内部的一个非线性运算单元,负责将神经元接收的加权输入信号转化为输出信号。在单个神经元层面上,激活函数的作用在于对输入信号进行非线性变换,从而使得整个网络具备更强大的表达能力和学习非线性关系的能力。
没有激活函数的多层神经网络本质上仅仅是线性模型的堆叠,无法捕捉复杂的模式。激活函数引入了非线性,使得即使在网络的深层结构中,组合的多层神经元也可以实现复杂的决策边界和抽象特征的学习。
激活函数的工作原理
- 加权和:每个神经元接收来自前一层神经元的加权输入信号,通常是通过求和的方式,也就是将每个输入信号乘以其对应的权重后再求和,有时还包括一个额外的偏置项(bias)。
- 非线性转换:将加权和后的信号传递给激活函数,激活函数对其进行处理,产生新的输出值。
- 输出:激活函数输出的结果作为本层神经元的输出,并作为下一层神经元的输入继续参与网络的计算。
激活函数的种类
可参考激活函数(sigmoid、tanh、ReLU、softmax)_sigmoid函数-CSDN博客
- sigmoid函数:它能够将输入值压缩到0和1之间,通常用于二分类问题的输出层。但是,它在输入值较大或较小时会出现梯度消失的问题,导致训练变得困难。
- Tanh函数(双曲正切函数):它将输入值压缩到-1和1之间,形状与Sigmoid类似,但是输出范围更广。Tanh同样存在梯度消失的问题。
- ReLU(Rectified Linear Unit):当输入大于0时输出等于输入,小于等于0时输出为0,有效缓解了梯度消失问题。
- Leaky ReLU:是对ReLU的改进版本,它是ReLU的一个变种,允许负值有一个很小的非零斜率,以解决ReLU在输入为负时梯度为零的问题。
- softmax归一化函数:二分类问题,经常使用sigmoid激活函数。而在处理多分类问题的时候,需要使用softmax函数。主要用于将一组任意实数值转化为概率分布的形式,且这些转化后的值满足归一化条件,即所有值的和为1,且每个值的范围都被限定在0到1之间。
具体而言,假设有一个K维向量Z = [z_1, z_2, ..., z_K],其中每个分量z_i可以是任意实数。通过softmax函数对其进行归一化处理后,得到的新向量P = [p_1, p_2, ..., p_K],每个分量p_i表示对应类别的概率,并且满足:
- 在这个公式中,每个分量p_i是原始值z_i经过指数函数变换后再除以所有分量指数函数变换后总和的结果。这样,即使输入的Z向量的分量具有非常大的动态范围,softmax函数也能保证输出的概率分布总是合法且具有比较性的。
- 在实践中,softmax函数常常被用作神经网络的最后一层激活函数,尤其是在多分类问题中,因为它能有效地将网络的输出转化为各个类别的概率预测,而且最大的那个p_i对应的类别往往被视为模型预测的类别。
六、损失函数
七、梯度、梯度爆炸、梯度消失
①梯度的定义
一元函数中,梯度就是函数的导数。
多元函数中,梯度是一个向量,描述了一个多元函数在其定义域内某一点所有变量上的方向导数的最大值。如对于一个多元函数 f(x),其中 x=(x1,x2,...,xn) 是一个 n 维向量,梯度记作∇f(x) 。
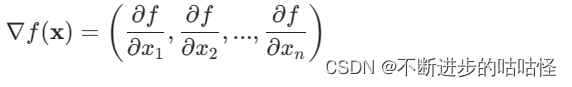
梯度不仅包含了每个变量的偏导数,还提供了函数在给定点上增长最快的方向(梯度的方向)以及增长的速率(梯度的模长)。
通过梯度下降算法,我们可以计算损失函数相对于模型参数的梯度,并依据梯度的负方向更新参数,从而逐步减少损失并优化模型性能。
总结:
- 它是一个向量,给出了函数在特定点处的变化趋势和最快变化方向。
- 在最优化问题中,梯度指引我们寻找最优解(最小化或最大化目标函数)的路径。
- 在机器学习中,梯度下降算法利用梯度信息更新模型权重,以期望最小化损失函数。
②梯度消失
梯度消失是深度学习领域中一种常见的问题,在训练深度神经网络时尤为突出,主要出现在使用反向传播算法更新网络参数的过程中。这个问题的核心在于:当误差信号从网络的最后一层反向传播到前面的层时,由于链式法则作用下的梯度连乘效应,导致梯度值随着网络深度的增加而急剧减小,直至趋于零。
具体过程: 在反向传播算法中,每个神经元的梯度是由其后一层所有神经元的梯度与它们之间的权重相乘后累加得到的。若激活函数的梯度在某些区域非常平缓(例如sigmoid函数在饱和区的梯度接近于0),并且网络层级较多时,连续多次的乘积运算将很容易导致梯度的累积效果趋向于零。这种情况下,网络前端的层几乎接收不到有效的梯度信号,进而无法进行有效的参数更新,这些层的学习就几乎停止了。
后果:
- 参数收敛困难:梯度消失意味着网络的前几层权重更新极其缓慢,即使经过很多次迭代,这些权重也很难达到最优解。
- 学习能力丧失:由于梯度消失,网络深层的特征难以被学习和利用,深层网络实际上失去了它应有的多层次抽象表示的能力,导致整个网络表现得像一个浅层网络。
- 训练失败:严重的情况下,梯度消失会导致整个网络无法进行有效的训练,即使有更多隐藏层也无法捕捉到更复杂的模式。
解决办法:
- 激活函数的选择:避免使用梯度饱和的激活函数,比如改用ReLU(Rectified Linear Unit)及其变体,它们在正区间内保持线性,不会出现梯度消失的情况。
- 权重初始化:采用合理的权重初始化策略,如Xavier初始化或He初始化,确保初始阶段梯度的传播能够维持在一个适中的范围内。
- 批量归一化(Batch Normalization, BN):BN层能够在每层训练过程中对输入数据做标准化处理,有效解决了内部协变量偏移问题,有助于稳定梯度的传播。
- 残差结构(Residual Connections):在深度残差网络中,直接添加从某层到后续层的快捷连接,使梯度可以直接绕过一些非线性变换,从而解决了深度网络中的梯度消失问题。
- 门控机制(如LSTM、GRU):在循环神经网络中,通过设计门控单元来控制信息流,以防止长期依赖关系中的梯度消失。
③梯度爆炸
梯度爆炸是在训练深度神经网络时可能出现的另一个挑战,它指的是在反向传播过程中,梯度值变得极大,以至于在更新网络权重时产生极端的、不稳定的变动。这种现象可能会导致以下问题:
具体过程: 在计算神经网络中各层参数梯度时,如果由于某种原因(如权重矩阵的元素异常大、学习率设置不当、激活函数的导数过大等),在反向传播中经过多层连续的乘法操作后,梯度的大小迅速增长到非常大的数值,甚至超出计算机浮点数表示范围,这就发生了梯度爆炸。
后果:
- 数值不稳定:梯度值过大时,更新权重时会产生巨大的步长,使得模型参数瞬间跳到远离最优解的位置,训练过程变得非常不稳定。
- NaN问题:当梯度值过大以至于溢出时,可能会导致数值计算结果变为
NaN(Not-a-Number),这意味着训练过程崩溃,无法继续进行下去。 - 过度拟合:虽然梯度爆炸不如梯度消失那么常见,但它同样会妨碍模型正常学习,可能导致模型过于复杂且对训练数据极为敏感,即过拟合。
解决办法:
- 梯度裁剪(Gradient Clipping):这是一种直接干预梯度大小的技术,当梯度的范数超过预设阈值时,将其重新缩放到一个合理的范围内。
- 权重约束与正则化:可以通过权重衰减(L2正则化)等方式来限制权重的增长,或者在模型训练中强制权重满足特定约束,如权重矩阵的范数不超过一定值。
- 学习率调度:合理设置学习率,并随着训练过程动态调整学习率,可以避免因初始学习率过大而导致的梯度爆炸。
八、梯度下降
①比喻:
想象你正在一座山峰上寻找山谷的最低点,即山脚下的那个位置。在这个场景中,你的眼睛暂时被蒙住,无法看到全局地形,只能依靠手里的指南针(梯度)来指导方向。
梯度就像是一个神奇的指南针,它能告诉你当前位置下坡最陡峭的方向。如果你站在山顶上,梯度将会指向山脚下坡最快的方向。每一步,你都会按照指南针指示的下坡方向走一段距离(这就是步长或学习率的概念),然后再次检查你现在的位置,重新计算下坡最陡的方向,继续前行。
在实际的机器学习和优化问题中:
- 山就是一个多维的“损失函数”。
- 你的位置则是模型参数的当前值。
- 山的高度代表损失函数的值。
- 迈步前进表示根据梯度更新参数。
- 看指南针代表计算梯度(损失函数的导数)。
关键定义:
- 梯度:就是在当前参数组合下,是当前参数点的斜率,损失函数值增大的最快方向(由于我们想让它减小,所以采取相反方向)。这里的梯度具有相对性,即梯度是损失函数相对于某个参数的梯度。
- 学习率:决定每次更新参数的幅度,学习率和梯度相乘就是步长。
通过反复迭代这个过程,你(模型)会逐渐朝着损失函数的最小值移动,最终找到或接近一个局部最小点,从而优化模型参数。
②梯度下降的基本思想是:
首先选择一个随机的初始点作为参数的起始值,然后在每一步迭代中,沿着该点损失函数梯度的负方向(即下降最快的方向)更新参数,以此来逐渐接近函数的最小值。
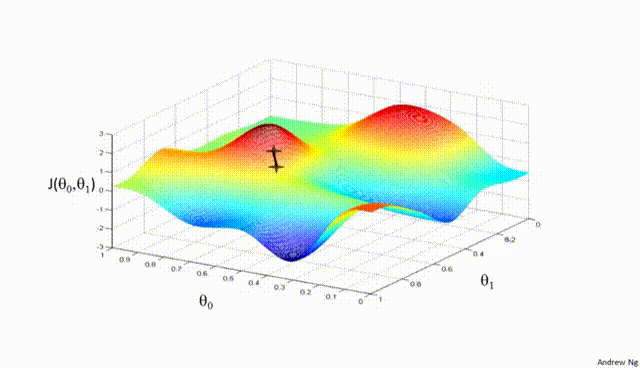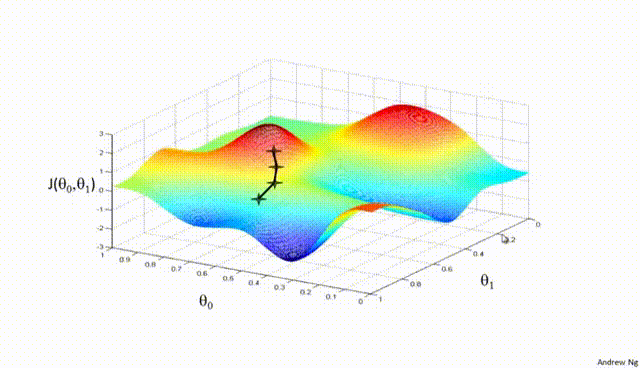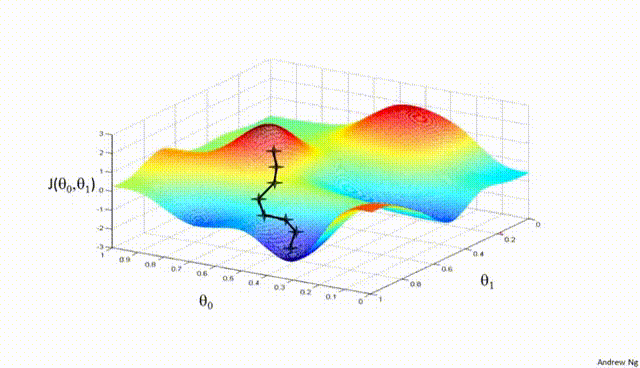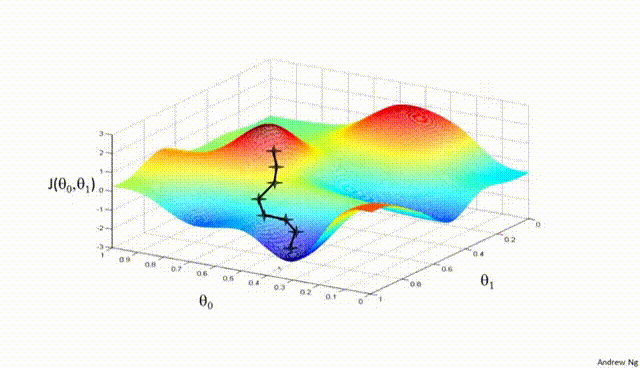
③数学公式

④梯度下降的步骤

⑤示例(以一元线性回归中的梯度下降为例)
这里,我们以简单的线性回归来进行说明。线性回归是一种基本的机器学习算法,用于建立自变量(输入)和因变量(输出)之间的线性关系。
在线性回归中,我们希望通过最小化均方误差(Mean Squared Error, MSE)来找到最佳拟合直线,其目标函数(损失函数)可以表示为:
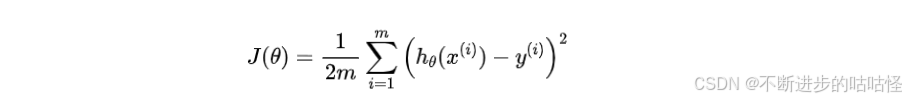
其中:

梯度可以表示为:
![]()
更新公式为:

九、常见梯度下降算法
史上最详细的梯度下降优化算法介绍(从SGD到Adam至Lookahead)_lookahead公式表达-CSDN博客
在机器学习模型训练时,模型优化算法是必不可少的,例如常见的梯度下降优化算法SGD,这也是大多数机器学习’炼丹师‘第一次接触机器学习时使用的优化算法,也是最容易理解的,但是机器学习任务中模型千变万化,很难做到一种优化算法“通吃”所有模型。因此对于不同的模型,需要对原始的梯度下降优化算法不断的改进优化。下面就对梯度下降优化等常见的优化算法及其改进算法做一一介绍。
9.1批梯度下降法(BGD)
批梯度下降法(batch gradient descent)是指在整个训练数据集上求解损失函数关于参数θ的梯度: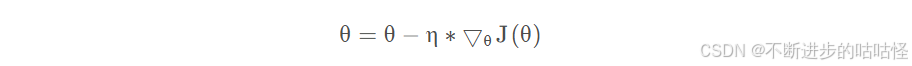
- η表示学习率,通常是一个较小的值,例如0.001,其决定我们将以多大的步长更新参数;
- ▽θJ(θ)表示损失函数在整个数据集上对参数θ计算一阶导数(取平均值)。因为是更新参数θ,所以计算θ的一阶导,一阶导方向是参数变化最快的方向。
由于每次更新时使用整个数据集计算所有梯度,因此计算速度非常慢,同时批梯度下降法不能在线更新模型,无法在运行过程中,增加新的样本。批梯度下降法代码如下:
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
代码理解:
for i in range(nb_epochs)::这是一个循环,表示我们要进行nb_epochs次迭代。在每次迭代中,我们都会更新模型的参数。
params_grad = evaluate_gradient(loss_function, data, params):这行代码计算了损失函数关于模型参数的梯度。evaluate_gradient是一个函数,它接受损失函数、数据和当前参数作为输入,返回梯度值。梯度表示损失函数在当前参数值下的变化方向。
params = params - learning_rate * params_grad:这行代码使用梯度下降算法更新模型的参数。我们沿着梯度的负方向更新参数,乘以一个学习率(learning_rate),以控制更新的步长。学习率是一个超参数,需要根据具体问题进行调整。
9.2随机梯度下降法(SGD)
批梯度下降法(stochastic gradient descent)是指使用每一条数据来计算梯度值更新参数: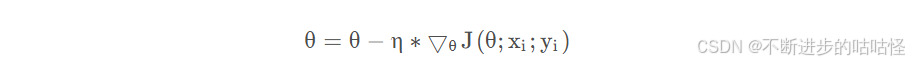
- η表示学习率,通常是一个较小的值,例如0.001,其决定我们将以多大的步长更新参数;
- ▽θJ(θ;xi;yi)表示损失函数在每一条数据上对参数θ计算一阶导数。因为是更新参数θ,所以计算θ的一阶导,一阶导方向是参数变化最快的方向。
通常,随机梯度下降法相比于批梯度下降法具有更快的速度,可用于在线学习,SGD以高方差频繁地更新,因此容易出现下列剧烈波动的情况。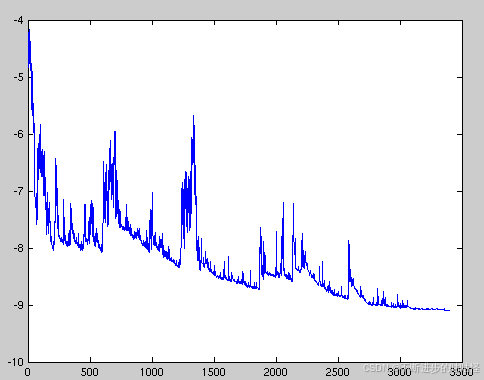
SGD优化算法的特点:
- 相比于批梯度下降法可能使得损失函数陷入局部的缺点,SGD的波动性使得其有可能收敛到更好的局部最优,
- 这也使得SGD收敛到局部最小值的过程变得更加复杂,因为SGD一直在震荡。
与批梯度下降法的优化代码相比,SGD只是在训练的轮次中,每次选择一个训练样本时多了一个for循环。
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad
9.3小批量梯度下降法
小批量梯度下降法(mini-batch gradient descent)综合了上述两种方法的优点,在每次训练时使用 n 个小批量样本进行更新: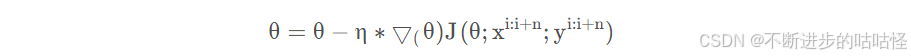
该方法的特点:
- 可以以更小的方差来更新参数,参数收敛的过程波动更小;
- 获得比批梯度下降法更快的运行速度。
对于小批量梯度下降的代码,只在小批量数据上计算梯度:
for i in range(nb_epochs):
np.random.shuffle(data):
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate*params_grd
- 选择一个合适的学习率是困难的。学习率太小会导致收敛太慢,太大会影响模型的收敛,有可能在最小值附近不断波动甚至偏离最小值。
- 对于不同的参数使用相同的学习率更新是不合理的。如果数据是稀疏的,就不能使用相同的学习率来更新了,对于出现次数少的特征,我们对其执行更大的学习率;
- 高度非凸误差函数普遍出现在神经网络中,在优化这类函数时,另一个关键的挑战是使函数避免陷入无数次优的局部最小值。Dauphin等人指出出现这种困难实际上并不是来自局部最小值,而是来自鞍点,即那些在一个维度上是递增的,而在另一个维度上是递减的。这些鞍点通常被具有相同误差的点包围,因为在任意维度上的梯度都近似为0,所以SGD很难从这些鞍点中逃开。
9.4梯度下降算法的优化算法
十、前向传播过程
前向传播(Forward Propagation)是指神经网络在接收到输入数据时,数据在网络中从输入层经过隐藏层(如果有多个的话)直至输出层的整个计算流程。
具体过程:
-
输入层:首先,输入数据(例如图像的像素值或文本的词嵌入向量)被送入网络的输入层。
-
隐藏层:数据在进入网络后,每一层神经元都会对其接收到的数据进行加权求和(此处的权重即为训练过程中待优化的参数),再加上一个偏置项,然后通过一个激活函数(如ReLU、sigmoid、tanh等)来引入非线性,生成该层的输出,即下一层的输入。
-
层间传递:这一过程在隐藏层之间递归进行,每一层神经元的输出作为下一层神经元的输入。
-
输出层:经过一系列隐藏层的处理后,数据到达输出层。输出层的激活值代表了模型对输入数据的预测结果,如分类问题中的各类别的概率,或者是回归问题中的预测值。
-
计算损失:前向传播的最后阶段通常会计算模型预测输出与实际目标值之间的差异,即损失函数(Loss Function)的值,这个值反映了模型预测的好坏程度。
十一、超参数(学习率、批次、层数)和参数(权重、偏置)
参数(Parameters)
-
定义: 参数是指模型内部学习到的变量,这些变量是在训练过程中通过最小化损失函数自动调整的。它们直接决定了模型的功能和预测能力。
-
特点:
- 自动学习: 在训练过程中,根据数据和选定的优化算法(如梯度下降),参数会不断更新以减少误差。
- 不需预先设定值: 参数的具体数值不是由开发者直接指定,而是通过训练过程得到。
- 示例: 神经网络中的权重(weights)和偏置(biases)就是典型的参数。
超参数(Hyperparameters)
-
定义: 超参数是关于模型结构或训练过程的配置选项,它们不能通过训练过程直接学到,而是在训练开始前由开发者根据经验、实验或特定策略来设置。
-
特点:
- 手动设置: 需要在训练之前人为确定,并且可能需要通过多次试验来找到最优值。
- 影响模型性能和训练效率: 合适的超参数选择可以显著提高模型的表现,反之则可能导致欠拟合或过拟合等问题。
- 示例:
- 学习率(Learning Rate): 决定了参数更新的速度。
- 批次大小(Batch Size): 每次迭代使用的样本数量。
- 网络层数(Number of Layers)和每层神经元数(Number of Neurons per Layer)。
- 正则化系数(Regularization Coefficients)等。
超参数调整方法:
超参数调整涉及选择合适的模型架构和训练配置。
- 手动搜索
- 网格搜索:通过遍历给定的参数网格,对每一组参数进行交叉验证,并选择平均性能最好的参数组合
- 随机搜索:在参数空间中随机选择参数组合,进行交叉验证,并选择平均性能最好的参数组合
- 贝叶斯优化:使用概率模型来预测超参数的性能,然后选择最有可能提高性能的参数组合进行评估
- 进化算法:模仿自然选择过程,通过对候选解决方案群体进行变异、交叉和选择操作逐步逼近最优解。适用于需要同时优化多个相互关联的超参数的情况
- 自动化超参数优化工具:如Google的AutoML、H2O.ai的Driverless AI、以及开源项目如Auto-sklearn、TPOT等,它们提供了自动化流程来进行特征工程、模型选择及超参数优化
参数调整方法:
参数调整主要是指通过训练过程自动完成的权重、偏置等内部变量的更新。通过反向传播算法根据训练数据的梯度信息自动调整,以最小化损失函数并提高模型的预测能力。
-
梯度下降及其变种:
- 批量梯度下降(Batch Gradient Descent):使用整个数据集来计算梯度。
- 随机梯度下降(Stochastic Gradient Descent, SGD):每次仅用一个样本来估计梯度,速度快但不稳定。
- 小批量梯度下降(Mini-batch Gradient Descent):结合了上述两种方法的优点,使用一个小批次的数据来计算梯度。
- 变种如动量(Momentum)、Adagrad、RMSprop、Adam等,这些算法通过不同的方式加速收敛并改善稳定性。
-
正则化技术:
- L1/L2正则化:通过惩罚较大的权重值来防止过拟合。
- Dropout:随机忽略部分神经元,减少复杂模型的过拟合风险。
- Early Stopping:当验证集上的性能不再提升时提前终止训练。
-
初始化策略:
- 适当的权重初始化(例如Xavier/Glorot初始化或He初始化)可以帮助加快收敛速度,并有助于避免梯度消失或爆炸问题。
十二、过拟合和欠拟合
-
欠拟合是指模型在训练集、验证集和测试集上均表现不佳的情况;
-
过拟合是指模型在训练集上表现很好,到了验证和测试阶段就很差,即模型的泛化能力很差
欠拟合产生原因:(1)模型复杂度过低;(2)特征量过少
过拟合产生原因:
(1)建模样本选取有误,导致选取的样本数据不足以代表预定的分类规则;
(2)例如对于决策树模型,如果我们对于其生长没有合理的限制,其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event),使其虽然可以完美匹配(拟合)训练数据,但是无法适应其他数据集
十三、独热编码
独热编码(One-Hot Encoding)是一种将分类或者离散型特征转化为数值型特征的方式,常用于机器学习和深度学习的数据预处理阶段。在独热编码中,每一个可能的类别或状态都会被表示为一个二进制向量(通常是长向量),向量的长度等于所有可能类别的总数。对于每一个具体的样本,其所属类别的向量位置会被赋值为1,而其他位置则为0。
例如,假设有一个特征有三个可能的类别:红、绿、蓝。对于一个特定样本,如果它是绿色,那么在独热编码后,会得到一个三维向量 [0, 1, 0],其中第二个位置代表绿色;如果是红色,则编码为 [1, 0, 0];若是蓝色,则编码为 [0, 0, 1]。
独热编码的主要优点在于:
- 它消除了类别之间潜在的顺序关系,因为每个类别都有自己独立的维度,不存在数值上的大小比较。
- 便于模型直接处理,许多机器学习算法(如逻辑回归、神经网络)可以直接接受这种二进制形式的输入。
- 明确区分出了每个类别,使得模型能够针对性地学习每个类别的特征。
然而,独热编码也会带来一些挑战,特别是当类别数量非常多时,可能会导致特征空间的维度急剧增加,从而产生稀疏矩阵和存储需求增大等问题。此外,过多的维度也可能影响模型训练速度和泛化性能。
十四、词嵌入序列
词嵌入序列(Word Embedding Sequence)是指在自然语言处理(NLP)中,将一段文本中的词汇通过词嵌入(Word Embedding)技术转化为一串连续的稠密向量序列的过程。具体来说:
-
对于文本中的每个单词,首先利用预训练好的词嵌入模型(如Word2Vec、GloVe或BERT等)将其转换为一个固定维度的向量,这个向量能够编码该单词在语义空间中的信息。
-
当完成文本中所有单词的词嵌入转换后,将这些单词对应的向量串联起来,形成一个向量序列。
例如,假设有一句话:“The cat sat on the mat。”这句话中的每个词经过词嵌入模型后可能变为如下向量:
- "The": [0.1, 0.2, 0.3, ...]
- "cat": [0.4, 0.5, 0.6, ...]
- "sat": [0.7, 0.8, 0.9, ...]
- "on": [1.0, 1.1, 1.2, ...]
- "the": [1.3, 1.4, 1.5, ...]
- "mat": [1.6, 1.7, 1.8, ...]
词嵌入序列就是把这些词向量按原句序排列起来形成的序列:
[[0.1, 0.2, 0.3, ...], [0.4, 0.5, 0.6, ...], [0.7, 0.8, 0.9, ...], [1.0, 1.1, 1.2, ...], [1.3, 1.4, 1.5, ...], [1.6, 1.7, 1.8, ...]]这样的词嵌入序列可以作为输入送入深度学习模型中进行后续的分析和处理,比如在序列标注、情感分析、机器翻译等任务中发挥重要作用。
十五、Scaling laws analysis
指对系统、过程或现象如何随其规模(大小、复杂度、输入量等)变化而变化进行的研究。这种分析方法旨在找出和理解在不同尺度上系统性能或结果与系统规模之间的数学关系或规律,即“规模法则”(scaling laws)。这些规律可以帮助预测当系统的某个参数(如尺寸、流量、能量等)按比例放大或缩小时,系统的其他关键属性(如成本、效率、响应时间等)会如何变化。
机器学习:近年来,"scaling laws"一词在深度学习领域特别流行,指的是研究模型性能(如准确率)如何随着模型大小(参数数量)、训练数据量等因素的增加而变化的规律。这项研究有助于指导构建更高效、大规模的机器学习模型。
十六、下游任务在evo中的具体体现
下游任务指的是在机器学习和人工智能领域中,利用预训练模型来解决的具体应用问题。在Evo这个案例中,模型首先通过无监督的预训练阶段学习到了大量基因组数据的统计规律,随后可以在多种生物学相关的下游任务中应用这些学到的知识,而不需要针对每项任务从头开始训练模型。以下是一些Evo能执行的下游任务实例:
-
零样本功能预测:Evo能够跨DNA、RNA和蛋白质三种分子生物学基本模式进行零样本功能预测。例如,它可以预测蛋白质功能突变的影响,评估非编码RNA和调控DNA序列的突变如何改变其功能。模型通过计算突变序列的似然性与实验测量的适应度分数之间的相关性,来衡量其预测性能。
-
多元素生成:Evo展示了在生成任务上的卓越能力,比如首次成功合成CRISPR-Cas分子复合物和完整的转座子系统。这展示了其在设计新颖生物分子结构方面的潜力。
-
基因必需性预测:利用整个基因组范围内的信息,Evo能以核苷酸分辨率预测基因是否为细胞生存所必需,这有助于理解基因的功能和疾病机理。
-
长序列生成:Evo能够生成长达650千碱基的富含编码序列的序列,远超以往方法,这对于合成生物学和基因工程有着重要应用价值。
-
特定序列设计和优化:例如,针对CRISPR-Cas9系统,Evo通过生成和筛选候选序列,结合AlphaFold2预测的蛋白质结构,来设计新型Cas9蛋白及其相应的tracrRNA和crRNA序列。类似地,对于IS200/IS605转座子系统,Evo通过微调后生成完整的转座子系统,进一步进行下游分析。
十七、适应度
在生物学和遗传学中,“fitness”(适应度)是一个关键概念,它描述的是一个生物体或其基因在特定环境中的生存和繁殖能力。
具体到分子生物学的语境,当提到蛋白质或核酸(如DNA、RNA)序列的“适应度”时,这通常意味着该序列在执行其生物功能方面的效率或效能。换句话说,适应度高的序列意味着它在细胞内能够更有效地促进所需生物过程,如蛋白质正确折叠、RNA剪接、基因表达调控等。
在Evo模型的研究中,适应度是通过实验方法如深度突变扫描(Deep Mutational Scanning, DMS)来测定的。DMS实验通过系统性地引入一系列突变到蛋白质编码序列中,并观察这些突变如何影响蛋白质的功能,功能的改变程度可以用一个量化指标——适应度得分来衡量。适应度得分越高,表示突变后的蛋白质在实验条件下表现得越好,可能是因为保持或增强了原有的功能,或者获得了新的有益特性。
Evo模型的性能评估部分涉及到将模型预测的序列似然性(或伪似然性)与这些实验获得的适应度得分进行对比。如果Evo能够准确预测哪些序列突变会导致高适应度(即良好的功能),则说明它在预测蛋白质或核酸序列功能变化方面具有很强的能力,即使在没有针对特定任务进行额外微调的情况下也能做到这一点。简言之,适应度在此处是一个衡量生物序列在进化或功能实验中表现好坏的度量标准。
十八、Baseline architectures(基准架构)
Baseline architectures(基准架构)是指在深度学习领域中,经过广泛验证和应用的一些预训练神经网络模型,它们可以作为其他任务的起点或基础。这些基准架构通常具有较高的准确性和鲁棒性,并且可以在许多不同的应用领域中使用。
以下是一些常见的基准架构:
-
VGG:VGG是一种基于卷积神经网络的图像分类模型,由Oxford的Visual Geometry Group开发。它使用了多个卷积层和池化层,并且每个卷积层的卷积核大小和步长都是固定的。VGG在ImageNet等大型图像数据集上取得了很好的性能,并且成为了许多图像分类任务的基准架构。
-
ResNet:ResNet是一种基于残差连接的卷积神经网络模型,由Microsoft Research的Kaiming He等人提出。它通过引入残差连接来解决深度神经网络中的梯度消失问题,使得网络可以更深层次地学习特征。ResNet在ImageNet等大型图像数据集上取得了很好的性能,并且成为了许多图像分类任务的基准架构。
-
Inception:Inception是一种基于多尺度卷积的卷积神经网络模型,由Google的Christian Szegedy等人提出。它通过使用不同大小的卷积核来学习不同尺度的特征,并且使用多个卷积层来捕捉不同层次的特征。Inception在ImageNet等大型图像数据集上取得了很好的性能,并且成为了许多图像分类任务的基准架构。
-
BERT:BERT是一种基于Transformer的预训练语言模型,由Google的Jacob Devlin等人提出。它通过使用大量的无标签文本数据来预训练模型,并且可以在许多自然语言处理任务中取得很好的性能。BERT在许多自然语言处理任务中取得了很好的性能,并且成为了许多自然语言处理任务的基准架构。
-
GPT:GPT是一种基于Transformer的预训练语言模型,由OpenAI的Timothy G.Brown等人提出。它通过使用大量的无标签文本数据来预训练模型,并且可以在许多自然语言处理任务中取得很好的性能。GPT在许多自然语言处理任务中取得了很好的性能,并且成为了许多自然语言处理任务的基准架构。
这些基准架构可以作为其他任务的起点或基础,并且可以在许多不同的应用领域中使用。通过使用这些基准架构,可以更快地开发出高性能的深度学习模型,并且可以更好地解决实际问题。
十九、长度单位换算
1m=10dm
=100cm
=1000mm
=1000 000 um
=1000 000 000 nm
=1000 000 000 000 pm
=1000 000 000 000 000 fm
而1 nm = 10 Å
所以1Å=10^(-10)m
二十、向量的向量积(矢积)和数量积(标积)的区别
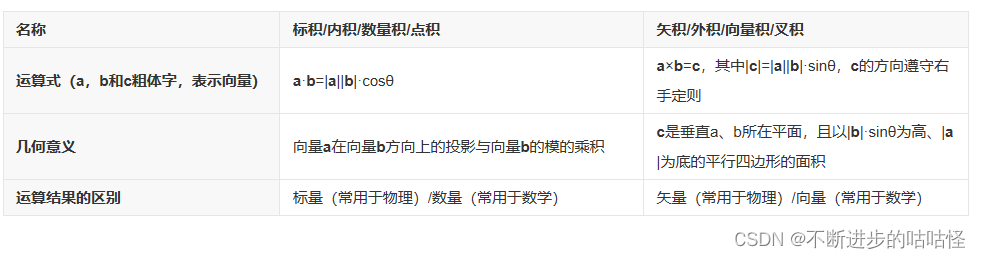
二十一、token是什么?
指代原始输入数据经过预处理后的基本单元。
NLP中是文本序列中最基本的离散单元,通常是一个词语、字符、子词(subword)或者是单词的一部分。在BERT、GPT等现代NLP模型中,还有一个特殊的token,即[CLS] token,它被用来标记句子的开头,用于整个句子级别的分类任务。
二十二、预训练和微调
预训练模型和微调模型是深度学习领域中常见的技术手段,尤其在自然语言处理(NLP)和生物信息学等领域得到广泛应用。这里以DNABERT为例说明:
预训练模型(Pre-trained Model)是指在大规模未标注数据上首先进行训练以获得通用知识和模式的模型。DNABERT作为基于Transformer的双向编码器表示模型,在开发阶段先利用从人类基因组抽取的大量无标签DNA序列进行训练。通过设计类似于BERT的方法,DNABERT运用多头自注意力机制捕获DNA序列中每个核苷酸与其周围上下文的关系,实现对DNA语言全局上下文的理解。在预训练过程中,DNABERT采用连续k个核苷酸组成的k-mer作为基本单元,随机遮蔽部分连续的k-mer序列(约占总序列的15%),然后让模型根据剩余序列来预测被遮蔽的部分,从而积累了大量的训练样本。模型通过交叉熵损失函数优化参数,形成一个初步掌握DNA基本语法和语义结构的预训练模型。
微调模型(Fine-tuning Model)则是指将预训练模型应用到具体任务上时,针对特定目标或问题进一步调整模型参数的过程。在DNABERT的应用场景下,预训练后的模型可以根据不同任务需求,如预测启动子、转录因子结合位点及剪接位点等,使用少量有标签的任务特异性数据进行微调。通过微调,模型能够适应具体任务的特征,并在此基础上提升对特定生物序列元素预测的准确性和效率,同时保持其原有的全局上下文理解能力。
总之,预训练模型提供了一个具有广泛适用性的基础框架,它通过对大规模未标注数据的学习获得了丰富的通用特征表达;而微调模型则是在预训练模型的基础上针对具体任务进行针对性训练,使其更加贴合实际应用场景的需求。
二十三、模型参数量
大模型的参数数量指的是模型中权重(w)和偏置(b)的数量。在神经网络模型中,权重和偏置是用于计算每个神经元输出的关键参数。权重决定了神经元之间连接的强度,而偏置则决定了神经元的激活阈值。这些参数在模型训练过程中通过反向传播算法从数据中学习得到,它们存储了模型从数据中学习到的知识和经验,也决定了模型的智能和性能。
参数数量越多,意味着模型中有更多的神经元,这些神经元之间的连接也更加复杂。因此,大模型通常具有更强的表达能力和更广泛的适应性,能够处理更复杂的任务。例如,OpenAI的GPT-3模型拥有1750亿个参数,这使得它能够在自然语言处理、文本生成等领域表现出卓越的能力。
然而,参数数量并不是衡量模型性能的唯一指标。模型的结构、训练数据、训练策略等因素也会对模型的性能产生影响。此外,参数数量的增加也会带来计算资源和存储空间的挑战,因此在实际应用中需要权衡各种因素来选择合适的模型。
二十四、全连接层
这里解释全连接层是如何处理输入的一维向量的。
在全连接层中,输入的一维向量会经过一系列线性和非线性变换,最终生成一个输出向量。这个过程可以分解为以下几个步骤:
-
线性变换:
-
全连接层首先将输入的一维向量与一个权重矩阵进行矩阵乘法运算。这个权重矩阵的大小通常是
[输出节点数, 输入向量长度]。在本例中,如果全连接层有64个节点,输入向量长度为经过池化和展平后的特征维度,那么权重矩阵的大小可能是[64, 池化后特征维度]。 -
矩阵乘法的结果是一个中间向量,其大小等于输出节点数(在这里是64)。
-
接着,全连接层还会加上一个偏置向量,这个偏置向量的大小与输出节点数相同(也是64)。偏置向量的每个元素都会分别加到中间向量的对应位置上。
-
-
非线性激活:
-
线性变换后的中间向量会作为输入传递给激活函数。在本例中,使用的激活函数是ReLU(Rectified Linear Unit)。
-
ReLU函数的定义是:对于所有的输入值,如果它是非负的,就保持不变;如果是负的,就将其置为0。数学表达式为:
f(x) = max(0, x)。 -
应用ReLU激活函数后,中间向量的每个元素都会被处理,负值会被置为0,非负值保持不变。这样处理后的向量就是全连接层的输出。
-
-
输出结果:
-
全连接层的输出是一个64维的向量。这个向量包含了网络从输入数据中提取的特征经过非线性变换后的信息。
-
这个输出向量通常会作为下一层(可能是另一个全连接层、输出层等)的输入,或者直接用于网络的最终预测任务。
-
通过这个过程,全连接层能够学习输入数据中的复杂模式和特征关系,并将这些信息以非线性方式映射到一个新的空间中。这使得全连接层在处理复杂的分类和回归任务时非常有用。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容
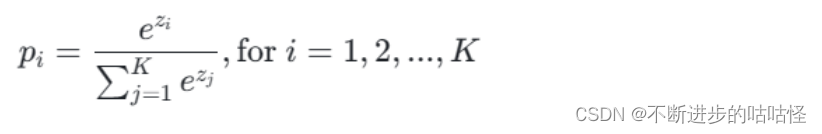







所有评论(0)