最近我们被客户要求撰写关于Lasso的研究报告，包括一些图形和统计输出。

此示例显示如何 lasso 识别和舍弃不必要的预测变量。

相关 视频：Lasso回归、岭回归等正则化回归数学原理及R语言实例

使用各种方法从指数分布生成 200 个五维数据 X 样本。

rng(3,'twister') %    实现可重复性

for i = 1:5    
    X(:,i) = exprnd
end

生成因变量数据 Y =  X *  r +  eps ，其中 r 只有两个非零分量，噪声 eps 正态分布，标准差为 0.1。

用 拟合交叉验证的模型序列 lasso ，并绘制结果。

Plot(ffo);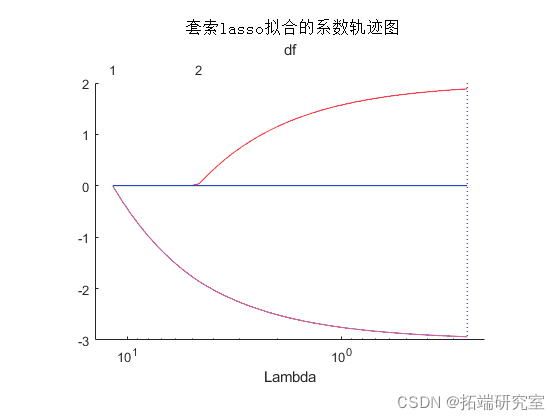

Lambda 该图显示了正则化参数的各种值的回归中的非零系数 。较大的值 Lambda 出现在图的左侧，意味着更多的正则化，导致更少的非零回归系数。

虚线代表最小均方误差的Lambda值（在右边），以及最小均方误差加一个标准差的Lambda值。后者是Lambda的一个推荐设置。这些线条只在你进行交叉验证时出现。通过设置'CV'名-值对参数来进行交叉验证。这个例子使用了10折的交叉验证。
 

图的上半部分显示了自由度（df），即回归中非零系数的数量，是Lambda的一个函数。在左边，Lambda的大值导致除一个系数外的所有系数都是0。在右边，所有五个系数都是非零的，尽管该图只清楚显示了两个。其他三个系数非常小，几乎等于0。

对于较小的 Lambda 值（在图中向右），系数值接近最小二乘估计。

求 Lambda 最小交叉验证均方误差加上一个标准差的值。检查 MSE 和拟合的系数 Lambda 。

MSE(lm)

b(:,lam)

lasso 很好地找到了系数向量 r 。

为了比较，求  r的最小二乘估计 。

rhat

估计 b(:,lam) 的均方误差略大于 rhat 的均方误差 。

res; % 计算残差
MSEmin 

但 b(:,lam) 只有两个非零分量，因此可以对新数据提供更好的预测估计。

---