欢迎指正。

研究计划写到心累，大家读过的关于机器学习的图像识别的综述类论文私我看一下啊。

一维正态分布推广到多维正态分布

推导过程中会加入推导所必需的理论

从一维标准正态分布说起，

二维标准正态分布的概率密度函数为：

接下来我们需要将其推广到一般化的正态分布上，考虑

接下来我们推导

二维连续随机变量的联合密度函数的推导
设二维随机变量

的联合密度函数为 ，如果函数

有连续（一阶）偏导数，且存在唯一（‘唯一’是一一对应的要求）的反函数：

，其变换的雅可比行列式：

综上，若

，则

的联合密度函数为

这个方法实际上就是二重积分的变量变换法。上面的

是

的反函数，不是乘积哈。

多维连续随机变量的联合密度函数
上面二维的联合密度函数推广到

维情况下为：

其实这里的

我们如果把它当作统计量，那么我们得到的就是统计量分布的密度函数，这一部分可以看茆诗松《高等数理统计》（第二版）的第25页。

其实大家能猜到接下来要干啥了吧？我们的

首先

参照公式（1）将上式中的

令

这就是

举两个例子来看一下：
比如说我们上面的

是一个正交阵，即对

做正交变换，则

互不相关。我们可以通过协方差矩阵来验证一下，此时

，有

，

之间的相关性为

。

一维情况下来看，

，

，则有

，就是我们常见的一维正态分布的密度函数。

用

计算

提前说明，我们这里说借助n维正态的性质并不是必需条件，因为其本质上其实就是个

稍作变换即为

这里补充一下高斯积分的内容，高斯积分

，证明过程如下：

记

，则

因此

.

用同样的方法以及积分的对称性，我们有以下几个结论：

上面三个公式中间的那个，

个相乘即为公式（3），所以在一开始就说，我们借助

维标准正态的性质，但不是必需的，因为我们通过

次高斯积分也可以算出来。

（当然，话也不能说死了，毕竟可能有更巧妙的办法能够借助n维标准正态分布继续算下去，欢迎评论指出）

借助上述高斯积分的性质，我们对公式（3）变形得到

对公式（4）,我们简记为

这个积分的思想是，我们假设这个球是圆葱（想象三维情况），我们积分求每一个半径

对应那一层的面积

（未知，我们需要后续慢慢算），然后计算从0到

所有层就是球的体积。按这个思想，这个n维球的体积应该是

，为啥上式我们要多一个

呢？因为我们不知道

的值，但是我们知道

的值，我们要通过

计算出我们需要的

.

接下来我们先给出

将公式（6）带入（5）得到

前面公式（4）我们知道

从而有

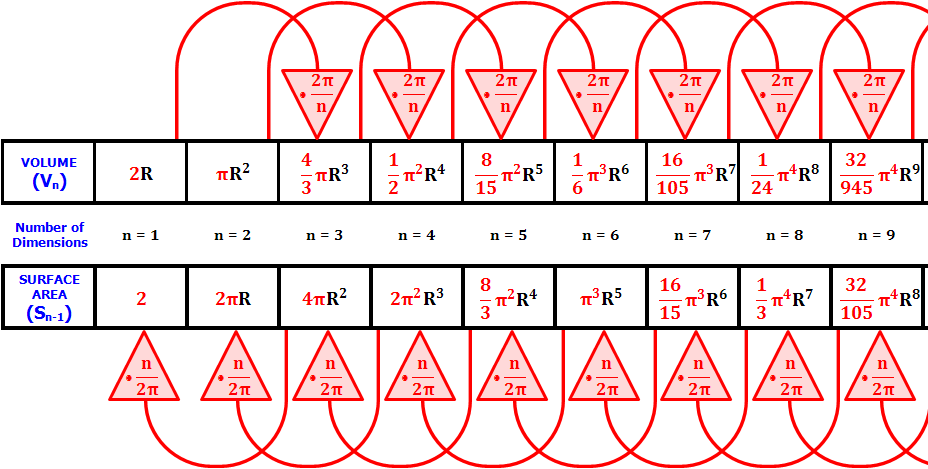
n维球的计算参考自https://spaces.ac.cn/archives/3154