离散PR控制器及逆变闭环性能验证(开源)
摘要:本文介绍了准PR控制器的离散化实现方法及其C语言编程。针对理想PR控制器在数字系统中的局限性,提出采用准PR控制器(带有限带宽)实现稳定控制。详细推导了双线性变换离散化过程,给出了归一化差分方程和完整的C语言实现代码(包括结构体定义、初始化函数和控制更新函数)。通过单相逆变器仿真验证,证明C语言实现的PR控制器与模块化实现效果一致,可直接移植到STM32、DSP等嵌入式平台。文中提供了仿真模
一、PR控制原理及离散化实现(C语言实现)
理想的PR控制器在共振频率(如50Hz或60Hz)处具有无限增益,但在数字控制系统中,这会引发数值不稳定、无法完全离散化共振项以及频率偏差和延时等问题。
为解决这些挑战,提出了准PR控制器(Quasi-PR或带限PR控制器),通过引入有限带宽近似实现共振效果,兼顾系统的可控性与可实现性。准PR控制器可实现正弦参考信号的无静差跟踪,广泛应用于电力电子变换器控制中。
嵌入式(STM32、DSP28335)中,要使用PR控制器需要将其离散化(C语言实现),因此本文将详细给出离散化的详细步骤、代码、开源的仿真模型。
1、准PR控制器传递函数
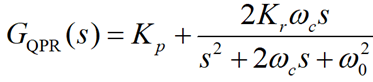
式中,Kp为比例系数,Kr为谐振系数,ω0为谐振角频率(目标频率,rad/s),ωc为截止带宽(rad/s),决定谐振峰宽度。
在单相逆变器应用中,ω0=2πfg,fg为电网频率即50Hz;ωc=(0.5∼5)%×ω0。Kp和Kr通常采取试凑法。
2、离散化实现(差分方程)
采用双线性变换(Tustin)离散化,将下式带入GQPR(s)。
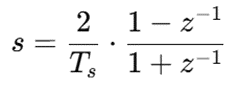
式中 Ts是采样周期。将GQPR(s)中 s替换后,就可以得到准PR控制器的差分形式,如下式
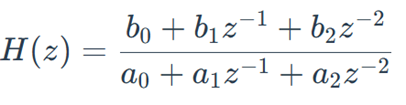
式中系数为
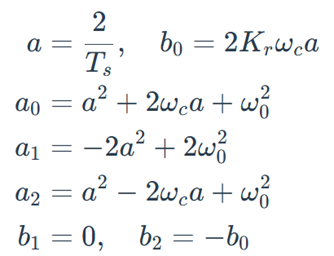
实际实现中通常使用归一化系数,将准PR控制器差分形式变为:
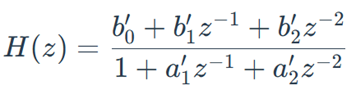
式中系数为
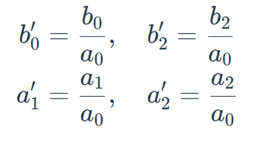
因此,可得到准PR控制器的差分方程为:
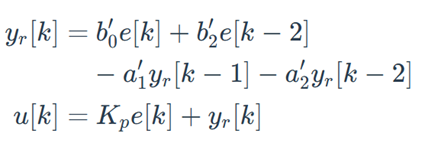
式中,e[k]为当前误差(参考值 - 反馈值),yr[k]为谐振部分输出,u[k]为控制器总输出
在嵌入式(STM32、DSP)中,可以根据上述准PR控制器的差分方程编写离散化PR控制器的C语言代码。
3、PR控制的C语言实现
#include <math.h>
// 准PR控制器结构体
typedef struct {
// 参数
float Kp; // 比例系数
float Kr; // 谐振系数
float w0; // 谐振角频率 (rad/s)
float wc; // 截止带宽 (rad/s)
float Ts; // 采样周期 (s)
// 离散化系数
float b0_prime;
float b2_prime;
float a1_prime;
float a2_prime;
// 状态变量
float e_prev1; // e[k-1]
float e_prev2; // e[k-2]
float yr_prev1; // yr[k-1]
float yr_prev2; // yr[k-2]
} QPRController;
// 初始化控制器
void QPR_Init(QPRController *ctrl,
float Kp, float Kr,
float w0, float wc,
float Ts)
{
ctrl->Kp = Kp;
ctrl->Kr = Kr;
ctrl->w0 = w0;
ctrl->wc = wc;
ctrl->Ts = Ts;
// 计算中间变量
float a = 2.0f / Ts;
float a_sq = a * a;
float w0_sq = w0 * w0;
float b0 = 2.0f * Kr * wc * a;
// 计算分母系数
float a0 = a_sq + 2.0f * wc * a + w0_sq;
float a1 = -2.0f * a_sq + 2.0f * w0_sq;
float a2 = a_sq - 2.0f * wc * a + w0_sq;
// 归一化系数
ctrl->b0_prime = b0 / a0;
ctrl->b2_prime = -b0 / a0; // b2 = -b0
ctrl->a1_prime = a1 / a0;
ctrl->a2_prime = a2 / a0;
// 初始化状态
ctrl->e_prev1 = 0.0f;
ctrl->e_prev2 = 0.0f;
ctrl->yr_prev1 = 0.0f;
ctrl->yr_prev2 = 0.0f;
}
// 执行控制计算
float QPR_Update(QPRController *ctrl, float ref, float fdb) {
// 计算当前误差
float e = ref - fdb;
// 计算谐振部分输出
float yr = ctrl->b0_prime * e
+ ctrl->b2_prime * ctrl->e_prev2
- ctrl->a1_prime * ctrl->yr_prev1
- ctrl->a2_prime * ctrl->yr_prev2;
// 比例部分 + 谐振部分
float u = ctrl->Kp * e + yr;
// 更新状态变量
ctrl->e_prev2 = ctrl->e_prev1;
ctrl->e_prev1 = e;
ctrl->yr_prev2 = ctrl->yr_prev1;
ctrl->yr_prev1 = yr;
return u;
}4、 使用示例
int main() {
QPRController pr_ctrl;
// 初始化参数 (示例:50Hz系统)
float Kp = 0.5f; // 比例系数
float Kr = 10.0f; // 谐振系数
float f0 = 50.0f; // 谐振频率 (Hz)
float w0 = 2 * M_PI * f0; // 角频率
float wc = 5.0f; // 截止带宽 (rad/s)
float Ts = 0.001f; // 1kHz采样
QPR_Init(&pr_ctrl, Kp, Kr, w0, wc, Ts);
// 实时控制循环
while(1) {
float ref = ...; // 获取参考值
float fdb = ...; // 获取反馈值
float u = QPR_Update(&pr_ctrl, ref, fdb);
// 应用控制量u到被控对象
...
delay(Ts); // 等待下一个采样周期
}
}二、仿真验证
图1展示了所搭建的单相逆变器闭环控制仿真模型,控制器采用PR控制策略,涵盖了基于模块搭建的PR控制器和C语言实现的PR控制器两种方式。
图2和图3分别给出了模块搭建的PR控制器与C语言实现的PR控制器的仿真结果。结果表明,两种实现方式在控制效果上一致,逆变器输出电感电流能够准确跟踪给定值,验证了C语言实现的PR控制器的有效性与可行性。
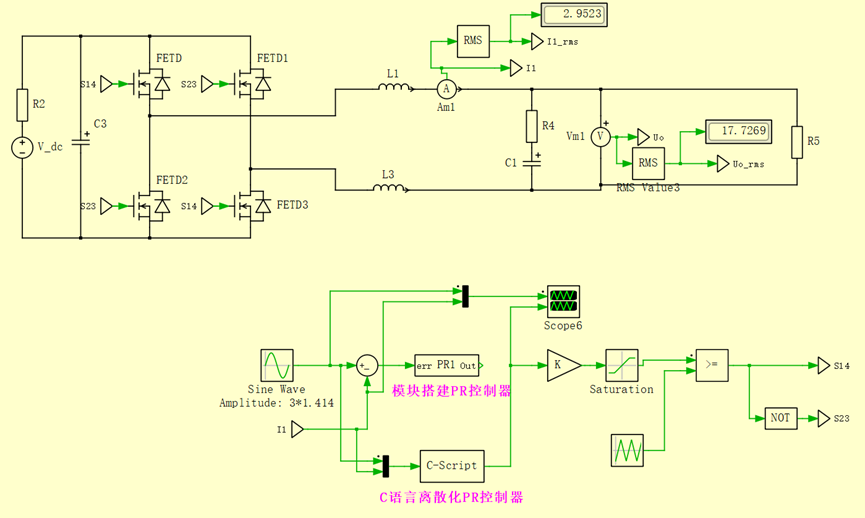
图 1 仿真模型截图
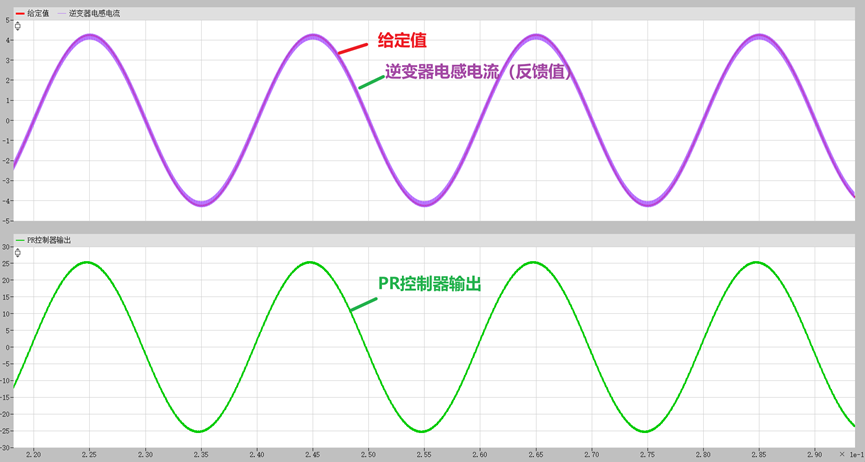
图 2 采用模块搭建的PR控制器的仿真结果
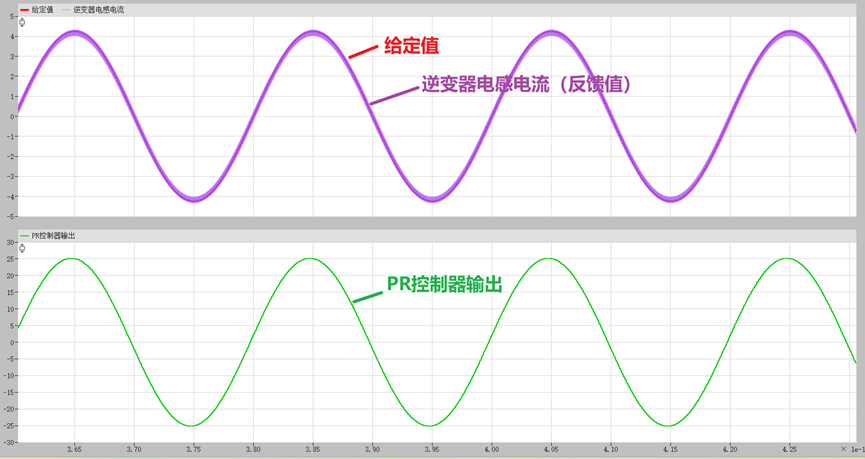
图 3 采用C语言实现的PR控制器的仿真结果
公众号“电源海盗船”中,回复“PR_Singlephase_inverter”我将发出这个仿真文件,包括单相逆变器闭环控制仿真模型、模块搭建的PR控制器、C语言实现的PR控制器。
C语言实现的PR控制器可直接移植到嵌入式(STM32、DSP28335)中!!!

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容








所有评论(0)