【Matlab数学建模】灰色预测模型
1982年我国学者邓聚龙教授发表第一篇中文论文《灰色控制系统》标志着灰色系统这一学科诞生。 白色系统是指一个系统的内部特征已知的,即系统的信息是完全充分的。黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。 灰色系统则介于二者之间。 选取参考数列:X0=X0(k)∣k=1,2,⋯ ,n=(X0(1),X0(2),⋯ ,X0(n)),其中k表示时刻
一、灰色预测的概念
1982年我国学者邓聚龙教授发表第一篇中文论文《灰色控制系统》标志着灰色系统这一学科诞生。
白色系统是指一个系统的内部特征已知的,即系统的信息是完全充分的。黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。
灰色系统则介于二者之间。
二、灰色关联度与优势分析
选取参考数列:
X0=X0(k)∣k=1,2,⋯ ,n=(X0(1),X0(2),⋯ ,X0(n)),其中k表示时刻 X_0 = {X_0(k)|k = 1, 2, \cdots, n} = (X_0(1), X_0(2), \cdots, X_0(n)), 其中k表示时刻 X0=X0(k)∣k=1,2,⋯,n=(X0(1),X0(2),⋯,X0(n)),其中k表示时刻
假设有m个比较数列:
Xi=Xi(k)∣k=1,2,⋯ ,n=(Xi(1),Xi(2),⋯ ,Xi(n)),(i=1,2,⋯ ,m) X_i = {X_i(k)|k = 1, 2, \cdots, n} = (X_i(1), X_i(2), \cdots, X_i(n)), (i = 1, 2, \cdots, m) Xi=Xi(k)∣k=1,2,⋯,n=(Xi(1),Xi(2),⋯,Xi(n)),(i=1,2,⋯,m)
则称:
ζi(k)=minimink∣X0(k)−Xi(k)∣+ρmaximaxk∣X0(k)−Xi(k)∣∣X0(k)−Xi(k)∣+ρmaximaxk∣X0(k)−Xi(k)∣ \zeta_i(k) = \frac{\min_i\min_k|X_0(k) - X_i(k)| + \rho \max_i\max_k|X_0(k) - X_i(k)|}{|X_0(k) - X_i(k)| + \rho \max_i\max_k|X_0(k) - X_i(k)|} ζi(k)=∣X0(k)−Xi(k)∣+ρmaximaxk∣X0(k)−Xi(k)∣minimink∣X0(k)−Xi(k)∣+ρmaximaxk∣X0(k)−Xi(k)∣
为比较数列Xi对参考数列X0在k时刻的关联系数。其中ρ∈[0,+∞)\rho\in [0, +\infty)ρ∈[0,+∞)为分辨系数,一般情况下ρ∈[0,1]\rho\in [0, 1]ρ∈[0,1]
关联系数ζ\zetaζ在每一时刻都有一个,过于分散,不利于比较,为此我们给出:
ri1n∑k=1nζi(k) r_i \frac1n\sum\limits^n_{k = 1}\zeta_i(k) rin1k=1∑nζi(k)
为比较数列Xi对参考数列X0的关联度。
然而关联系数公式中的∣X0(k)−Xi(k)∣|X_0(k) - X_i(k)|∣X0(k)−Xi(k)∣并不能去别处因素关联是正关联还是负关联,可采用以下方法解决该问题,记:
σi=∑k=1nkXi(k)−∑k=1nXi(k)∑k=1nknσn=∑k=1nk2−(∑k=1nk)2n \sigma_i = \sum\limits^n_{k = 1}kX_i(k) - \sum\limits^n_{k = 1}X_i(k)\sum\limits^n_{k = 1}\frac k n \sigma_n = \sum\limits^n_{k = 1}k^2 - \frac{(\sum\limits^n_{k = 1}k)2}{n} σi=k=1∑nkXi(k)−k=1∑nXi(k)k=1∑nnkσn=k=1∑nk2−n(k=1∑nk)2
则当sign(σiσn)=sign(σjσn)sign(\frac{\sigma_i}{\sigma_n}) = sign(\frac{\sigma_j}{\sigma_n})sign(σnσi)=sign(σnσj),则Xi和Xj为正关联,否则为负关联。
代码实现:
function [zeta, r] = func(x, x_0, rho)
[m, ~] = size(x);
if nargin < 3
rho = 0.5;
end
if nargin < 2
x_0 = max(x);
end
x_abs = abs(x_0 - x);
mn = min(min(x_abs));
mx = max(max(x_abs));
zeta = (mn + rho * mx) ./ (abs(repmat(x_0, m, 1) - x) + rho * mx);
r = mean(zeta, 2);
end
三、灰色生成数列
累加生成:
设原始数列:x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(n))x(0)的一次累加数列:x(1)(k)=∑i=1kx(0)(i),k=1,2,⋯ ,n,x(1)=(x(1)(1),x(1)(2),⋯ ,x(1)(n))x(0)的r次累加数列:x(r)(k)=∑i=1kx(r−1)(i),k=1,2,⋯ ,n,r≥1 设原始数列:x^{(0)} = (x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n))\\ x^{(0)}的一次累加数列:x^{(1)}(k) = \sum^k_{i = 1}x^{(0)}(i), k = 1, 2, \cdots, n, \\ x^{(1)} = (x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n))\\ x^{(0)}的r次累加数列:x^{(r)}(k) = \sum^k_{i = 1}x^{(r - 1)}(i), k = 1, 2, \cdots, n, r ≥ 1 设原始数列:x(0)=(x(0)(1),x(0)(2),⋯,x(0)(n))x(0)的一次累加数列:x(1)(k)=i=1∑kx(0)(i),k=1,2,⋯,n,x(1)=(x(1)(1),x(1)(2),⋯,x(1)(n))x(0)的r次累加数列:x(r)(k)=i=1∑kx(r−1)(i),k=1,2,⋯,n,r≥1
累减生成:
设原始数列:x(1)=(x(1)(1),x(1)(2),⋯ ,x(1)(n))x(1)的一次累减数列:x(0)(k)=x(1)(k)−x(1)(k−1),k=2,3,⋯ ,n, 设原始数列:x^{(1)} = (x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n))\\ x^{(1)}的一次累减数列:x^{(0)}(k) = x^{(1)}(k) - x^{(1)}(k - 1), k = 2, 3, \cdots, n, 设原始数列:x(1)=(x(1)(1),x(1)(2),⋯,x(1)(n))x(1)的一次累减数列:x(0)(k)=x(1)(k)−x(1)(k−1),k=2,3,⋯,n,
function res = func(a, r)
% a为原始数列
% 若r为正数,则res为a的+r次累加数列
% 若r为负数,则res为a的-r次累减数列
if r == 0
res = a;
return
end
n = length(a);
if r > 0
a = func(a, r - 1);
res = cumsum(a);
return
end
if r < 0
a = func(a, r + 1);
res = a - [0, a(1 : length(a) - 1)];
return
end
end
加权邻值生成
设原始数列:x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(n)) 设原始数列:x^{(0)} = (x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n))\\ 设原始数列:x(0)=(x(0)(1),x(0)(2),⋯,x(0)(n))
称x(0)(k−1),x(0)(k)x^{(0)}(k-1), x^{(0)}(k)x(0)(k−1),x(0)(k)为原始数列的任意一对邻值。x(0)(k−1)x^{(0)}(k-1)x(0)(k−1)为后邻值,x(0)(k)x^{(0)}(k)x(0)(k)为前邻值。对于常数α∈[0,1]\alpha\in[0, 1]α∈[0,1],设有:
z(0)(k)=αx(0)(k)+(1−α)x(0)(k−1),k=2,3,⋯ ,n, z^{(0)}(k) = \alpha x^{(0)}(k) + (1 - \alpha)x^{(0)}(k - 1), k = 2, 3, \cdots, n, z(0)(k)=αx(0)(k)+(1−α)x(0)(k−1),k=2,3,⋯,n,
将数列z(0)z^{(0)}z(0)称为数列x(0)x^{(0)}x(0)在权α\alphaα下的邻值生成数,α\alphaα被称为生成系数。
特别地,若α=0.5\alpha = 0.5α=0.5,则称:
z(0)(k)=0.5x(0)(k)+0.5x(0)(k−1),k=2,3,⋯ ,n, z^{(0)}(k) = 0.5x^{(0)}(k) + 0.5x^{(0)}(k - 1), k = 2, 3, \cdots, n, z(0)(k)=0.5x(0)(k)+0.5x(0)(k−1),k=2,3,⋯,n,
为均值生成数,也称等权邻值生成数。
function z = func(x, alpha)
if nargin < 2
alpha = 0.5;
end
a = alpha * x;
b = [0, (1 - alpha) * x(1 : length(x) - 1)];
z = a + b;
end
四、灰色模型GM(1, 1)
① 灰色预测的相关概念
G代表grey(灰色),M代表model(模型)
设原始数列:
x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(n) x^{(0)} = (x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n) x(0)=(x(0)(1),x(0)(2),⋯,x(0)(n)
x(0)x^{(0)}x(0)的一次累加数列:
x(1)(k)=∑i=1kx(0)(i),k=1,2,⋯ ,n,x(1)=(x(1)(1),x(1)(2),⋯ ,x(1)(n)) x^{(1)}(k) = \sum^k_{i = 1}x^{(0)}(i), k = 1, 2, \cdots, n, \\ x^{(1)} = (x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n))\\ x(1)(k)=i=1∑kx(0)(i),k=1,2,⋯,n,x(1)=(x(1)(1),x(1)(2),⋯,x(1)(n))
定义x(1)x^{(1)}x(1)的灰导数为:
d(k)=x(0)(k)=x(1)(k)−x(1)(k−1) d(k) = x^{(0)}(k) = x^{(1)}(k) - x^{(1)}(k - 1) d(k)=x(0)(k)=x(1)(k)−x(1)(k−1)
令z(1)z^{(1)}z(1)为数列x(1)x^{(1)}x(1)的邻值生成数列,即:
z(1)(k)=αx(1)(k)+(1−α)x(1)(k−1) z^{(1)}(k) = \alpha x^{(1)}(k) + (1 - \alpha)x^{(1)}(k - 1) z(1)(k)=αx(1)(k)+(1−α)x(1)(k−1)
于是定义GM(1, 1)的灰微分方程模型为:
d(k)+az(1)(k)=bx(0)(k)+az(1)(k)=b d(k) + az^{(1)}(k) = b\\ x^{(0)}(k) + az^{(1)}(k) = b d(k)+az(1)(k)=bx(0)(k)+az(1)(k)=b
其中x(0)(k)x^{(0)}(k)x(0)(k)称为灰导数,a称为发展系数,z(1)(k)z^{(1)}(k)z(1)(k)称为白化背景值,a称为灰作用量。
取k=2,3,⋯ ,n,k = 2, 3, \cdots, n,k=2,3,⋯,n,由灰微分方程可得:
{d(2)+az(1)(2)=bd(3)+az(1)(3)=b⋯⋯⋯⋯⋯⋯d(n)+az(1)(n)=b \left\{ \begin{aligned} d(2) + az^{(1)}(2) = b\\ d(3) + az^{(1)}(3) = b\\ \cdots\cdots\cdots\cdots\cdots\cdots\\ d(n) + az^{(1)}(n) = b\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧d(2)+az(1)(2)=bd(3)+az(1)(3)=b⋯⋯⋯⋯⋯⋯d(n)+az(1)(n)=b
引入矩阵:
u=(ab) u = \begin{pmatrix} a\\ b\\ \end{pmatrix} u=(ab)
Y=(x(0)(2)x(0)(3)⋮x(0)(n)) Y = \begin{pmatrix} x^{(0)}(2)\\ x^{(0)}(3)\\ \vdots\\ x^{(0)}(n)\\ \end{pmatrix} Y=⎝⎜⎜⎜⎛x(0)(2)x(0)(3)⋮x(0)(n)⎠⎟⎟⎟⎞
B=(−z(1)1−z(2)1⋮⋮−z(n)1) B = \begin{pmatrix} -z^{(1)} & 1\\ -z^{(2)} & 1\\ \vdots&\vdots\\ -z^{(n)} & 1\\ \end{pmatrix} B=⎝⎜⎜⎜⎛−z(1)−z(2)⋮−z(n)11⋮1⎠⎟⎟⎟⎞
于是GM(1, 1)模型可以表示为:
Y=Bu Y = Bu Y=Bu
u^=(a^b^)=(BTB)−1BTY \hat{u} = \begin{pmatrix} \hat{a}\\ \hat{b}\\ \end{pmatrix}= (B^TB)^{-1}B^TY u^=(a^b^)=(BTB)−1BTY
对于GM(1, 1)的灰微分方程,如果将x(0)(k)x^{(0)}(k)x(0)(k)的时刻k换成连续变量t,则对应的白微分方程即是:
dx(1)(t)dt+ax(1)(t)=b \frac{dx^{(1)}(t)}{dt} + ax^{(1)}(t) = b dtdx(1)(t)+ax(1)(t)=b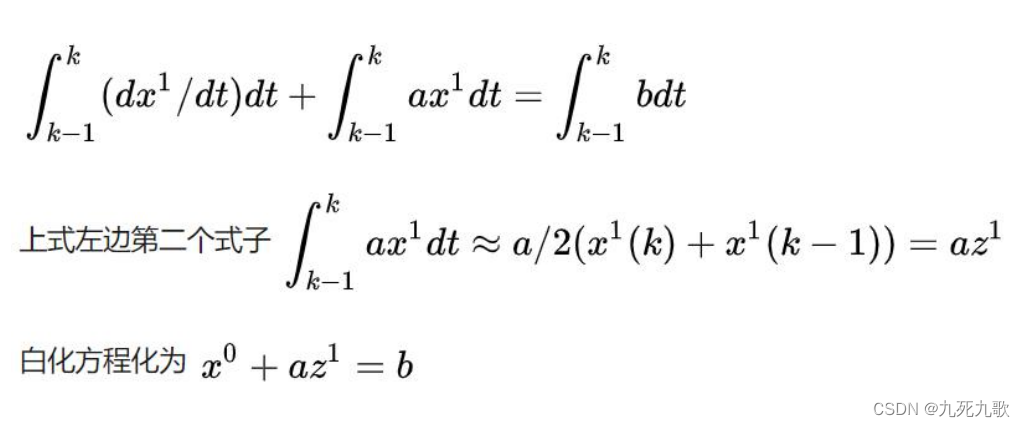
② 灰色预测的步骤
第一步:级比检验
设原始数列为:
x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(n) x^{(0)} = (x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n) x(0)=(x(0)(1),x(0)(2),⋯,x(0)(n)
计算数列的级比:
λ(k)=x(0)(k−1)x(0)(k) \lambda(k) = \frac{x^{(0)}(k - 1)}{x^{(0)}(k)} λ(k)=x(0)(k)x(0)(k−1)
如果所有的级比都落在可覆盖区间X=(e−2n+1,e2n+1)X = (e^{\frac{-2}{n + 1}}, e^{\frac{2}{n + 1}})X=(en+1−2,en+12)内,则原始数列x(0)x^{(0)}x(0)可以建立GM(1, 1)模型并进行灰色预测,否则需要对数据进行变化处理,如平移变化:
取c使得数列:y(0)(k)=x(0)+c,k=1,2,⋯ ,n,∀k∈Z+,y(0)(k)∈(e−2n+1,e2n+1) 取c使得数列:\\ y^{(0)}(k) = x^{(0)} + c, k = 1, 2, \cdots, n, \\ \forall k \in Z_+, y^{(0)}(k) \in (e^{\frac{-2}{n + 1}}, e^{\frac{2}{n + 1}}) 取c使得数列:y(0)(k)=x(0)+c,k=1,2,⋯,n,∀k∈Z+,y(0)(k)∈(en+1−2,en+12)
第二步:建立GM(1, 1)模型
原始数列为:
x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(n) x^{(0)} = (x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n) x(0)=(x(0)(1),x(0)(2),⋯,x(0)(n)
为它建立GM(1, 1)模型:
x(0)(k)+az(1)(k)=b x^{(0)}(k) + az^{(1)}(k) = b x(0)(k)+az(1)(k)=b
对应的白化模型是:
dx(1)(t)dt+ax(1)(t)=b \frac{dx^{(1)}(t)}{dt} + ax^{(1)}(t) = b dtdx(1)(t)+ax(1)(t)=b
该微分方程的解是:
x(1)(t)=(x(0)(1)−ba)e−a(t−1)+ba x^{(1)}(t) = (x^{(0)}(1) - \frac b a)e^{-a(t - 1)} + \frac b a x(1)(t)=(x(0)(1)−ab)e−a(t−1)+ab
于是便能得到预测值:
x^(1)(k+1)=(x(0)(1)−ba)e−ak+ba,k=1,2,⋯ ,n−1x^(0)(k+1)=x^(1)(k+1)−x^(1)(k),k=1,2,⋯ ,n−1 \hat{x}^{(1)}(k + 1) = (x^{(0)}(1) - \frac b a)e^{-ak} + \frac b a, k = 1, 2, \cdots, n - 1\\ \hat{x}^{(0)}(k + 1) = \hat{x}^{(1)}(k + 1) - \hat{x}^{(1)}(k), k = 1, 2, \cdots, n - 1 x^(1)(k+1)=(x(0)(1)−ab)e−ak+ab,k=1,2,⋯,n−1x^(0)(k+1)=x^(1)(k+1)−x^(1)(k),k=1,2,⋯,n−1
function [u, f] = func(x, alpha)
% x是原始数列
% alpha是生成系数,默认为0.5
% f是预测数列的一次生成数列的函数
if nargin < 2
alpha = 0.5;
end
x_1 = cumsum(x);
z = alpha * x_1(2 : end) + (1 - alpha) * x_1(1 : end - 1);
u = [-z; ones(1, length(x) - 1)]' \ x(2 : end)';
f = @(k) (x(1) - u(2) /u(1)) * exp(-u(1) * k + u(1)) + u(2) / u(1);
end
第三步:检验预测值
① 残差检验:
称:
ε(k)=x(0)(k)−x^(0)(k)x(0)(k),k=1,2,⋯ ,n ε(k) = \frac{x^{(0)}(k) - \hat{x}^{(0)}(k)}{x^{(0)}(k)}, k = 1, 2, \cdots, n ε(k)=x(0)(k)x(0)(k)−x^(0)(k),k=1,2,⋯,n
为相对残差
如果对∀k=1,2,⋯ ,n,∣ε(k)<0.1∣对\forall k = 1, 2, \cdots, n, |ε(k) < 0.1|对∀k=1,2,⋯,n,∣ε(k)<0.1∣,则认为达到较高的要求。否则,若对∀k=1,2,⋯ ,n,∣ε(k)<0.2∣对\forall k = 1, 2, \cdots, n, |ε(k) < 0.2|对∀k=1,2,⋯,n,∣ε(k)<0.2∣,则认为达到一般要求。
② 级比偏差值检验
计算:
ρ(k)=1−1−0.5a1+0.5aλ(k) \rho(k) = 1 - \frac{1 - 0.5a}{1 + 0.5a}\lambda(k) ρ(k)=1−1+0.5a1−0.5aλ(k)
如果对∀k=2,3,⋯ ,n,∣ρ(k)<0.1∣对\forall k = 2, 3, \cdots, n, |\rho(k) < 0.1|对∀k=2,3,⋯,n,∣ρ(k)<0.1∣,则认为达到较高的要求。否则,若对∀k=2,3,⋯ ,n,∣ρ(k)<0.2∣对\forall k = 2, 3, \cdots, n, |\rho(k) < 0.2|对∀k=2,3,⋯,n,∣ρ(k)<0.2∣,则认为达到一般要求。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)