1 简介

针对模拟网络病毒的传播,提出基于元胞自动机模型的网络病毒传播的方法.将病毒的传播过程分为2个阶段,并分别对不同的阶段建模.经过仿真,可以获得不同状态的计算机系统的数量,病毒的数量和病毒传播趋势等信息.结果表明,用元胞自动机模型仿真病毒传播能够更清晰地反映出网络病毒传播的趋势,与实际病毒传播符合较好.

1.1 元胞自动机

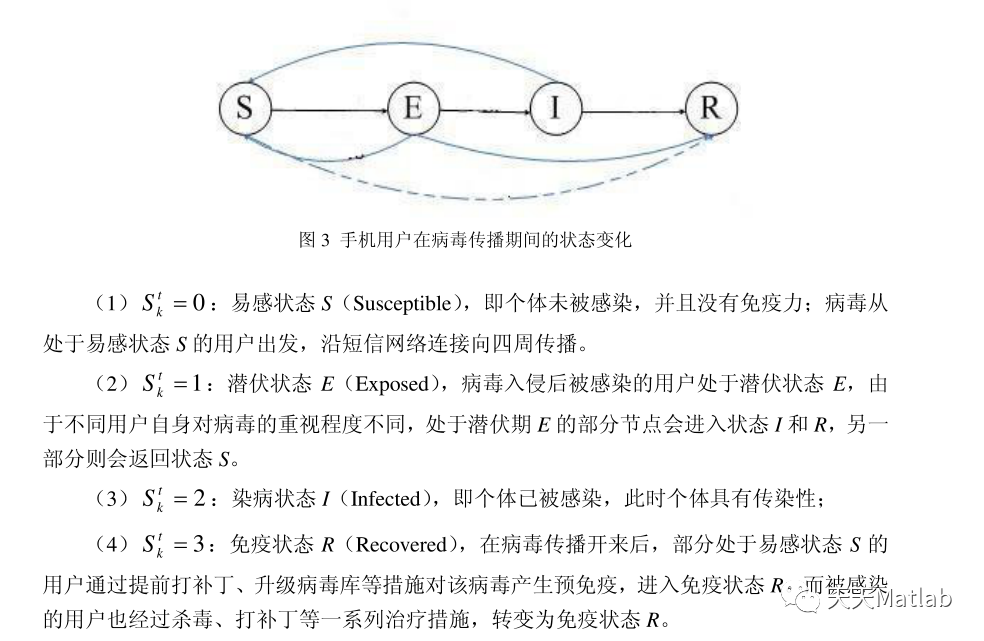
1.2 短信网络中病毒传播的元胞自动机模型

2 部分代码

function Message_Spread_Mode
tic
load 'Data\Link.txt';   %读入连接矩阵
% load '\Data\Point_X.txt'; %读入横坐标
% load '\Data\Point_Y.txt'; %读入纵坐标
%-------------------------------------------------------------------------%
%状态分布及状态转移概率SEIR
%0:易感状态S（Susceptible） P_0_1; （P_0_3:预免疫系数）
%1:潜伏状态E（Exposed）     P_1_0；P_1_2；P_1_3
%2:染病状态I（Infected）     P_2_0；P_2_3
%3:免疫状态R（Recovered）   P_3_0
%-------------------------------------------------------------------------%
%计算各用户节点的度                                                          
De=sum(Link);                                                             %用户节点的度
%------------——————----参数设置与说明--------------------------------%
[M N]=size(Link);                                                         %连接矩阵的规模
I_E=0.6;                                                                   %潜伏期E用户的传染强度
I_I=0.9;                                                                   %发病期I用户的传染强度
lamda=sum(De)/M;                                                           %用户单位时间内平均发送信息的数量
%P_m1：用户预免疫系数
%State：用户所处状态State=zeros(1,M);0:表示易感状态（Susceptible）
%---------------------------------1---------------------------------------%
%先讨论用户预免疫系数P_m1对病毒传播的影响
p(-De(j)))         %向免疫状态R转移
                                  State(t,j)=3;
                                  TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1
                              else
                                  State(t,j)=State(t-1,j);       %状态不变，依然为潜伏期E（1）
        %此时用户维持在原状态I
                              TimeLong_F(j)=TimeLong_F(j)+2;
                          else
                              %此时用户对进行杀毒并升级病毒库，进入免疫状态R
                              State(t,j)=3;
                              TimeLong_F(j)=0; %处于感染期（中毒状态）的时间长度
                              TimeLong_E(j)=1; %进入免疫期的时间长度
                          end
                      else
                          %此时用户处于免疫期
                          if TimeLong_E<=G_t         %病毒此时并未突变，维持原状态R（免疫状态）
                              State(t,j)=State(t-1,j);
                              TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
                          else
                              if rand<=1/G_t             %病毒突变，状态转移为易感状态S
                                  State(t,j)=0;
                                  TimeLong_E(j)=0;
                              else
                                  %此时用户状态依然不变
                                  State(t,j)=State(t-1,j);
                                  TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
                              end
                          end
                      end
                  end
              end
          end
      end
      %统计各状态的节点数量
      Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量
      Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量
      Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量
      Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量
      figure(i+10)
      if rem(t,3)==0
          plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold on
          plot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold on
          plot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold on
          plot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold on
      else
          continue;
      end
      legend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')
      xlabel('模拟时间')
      ylabel('各状态的人口数量')
  end
end
toc

3 仿真结果

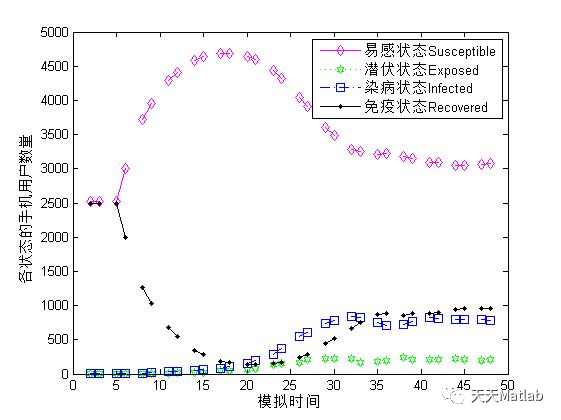
4 参考文献

[1]宋玉蓉, & 蒋国平. (2009). 基于一维元胞自动机的复杂网络恶意软件传播研究. 物理学报(09), 5911-5918

### 博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，有科研问题可私信交流。

**部分理论引用网络文献，若有侵权联系博主删除。**