【数学建模】图论模型(基础理论+最大流与最小费用流问题)
定理 给定图 G=(V,E)G=(V,E)G=(V,E),所有顶点的度数之和是边数的2倍,即∑v∈Vd(v)=2∣E∣\sum_{v \in V} d(v)=2|E|v∈V∑d(v)=2∣E∣对于无向图,关联矩阵 M=(mij)n×m\boldsymbol{M}=\left(m_{i j}\right)_{n \times m}M=(mij)n×m:mij={1,vi 与 ej 相关联, 0
图论模型
基础理论
1.无向图与有向图
- 有向图的边称为弧,有向图一般记为 D=(V,A)D=(V,A)D=(V,A),其中 VVV 为顶点集,AAA 为弧集。
- 边的表示 (vi,vj)(v_i,v_j)(vi,vj),弧的表示 <vi,vj><v_i,v_j><vi,vj>。
2.简单图与完全图
- 无环且无重边的图称为简单图。
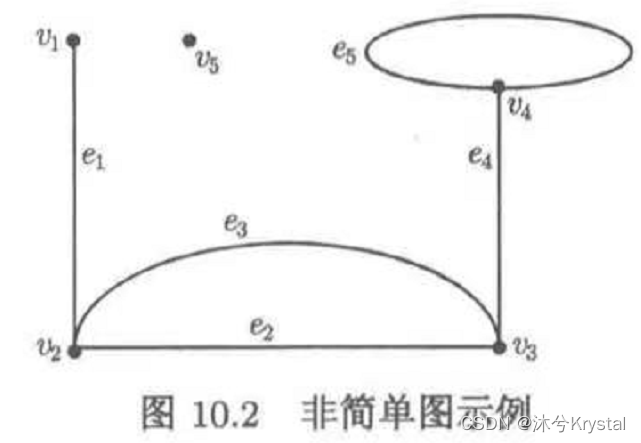
- 上图中,e2e_2e2 和 e3e_3e3 为重边, e5e_5e5 为环。
- 任意两点均相邻的简单图称为完全图。含 nnn 个顶点的完全图记为 KnK_nKn.
3.赋权图
- 赋权图中的权可以是距离、费用、时间、效益、成本等。
4.顶点的度
- 出度记为 d+(v)d^+(v)d+(v),入度记为 d−(v)d^-(v)d−(v).
- 度数为奇数的顶点称为奇顶点,度为偶数的顶点称为偶顶点。
定理 给定图 G=(V,E)G=(V,E)G=(V,E),所有顶点的度数之和是边数的2倍,即
∑v∈Vd(v)=2∣E∣ \sum_{v \in V} d(v)=2|E| v∈V∑d(v)=2∣E∣
5.子图
- 如果 G1G_1G1 是 G2G_2G2 的子图,且 V1=V2V_1=V_2V1=V2,则称 G1G_1G1 是 G2G_2G2 的生成子图。
6.道路与回路
- 设 W=v0e1v1e2...ekvkW=v_0e_1v_1e_2...e_kv_kW=v0e1v1e2...ekvk,路长为边的个数 kkk
- 各边相异的道路称为迹,各顶点相异的道路称为轨道。
- 以顶点 u,vu,vu,v 分别为起点和终点的最短轨道之长为顶点 u,vu,vu,v 的距离。
7.连通图与非连通图
- 如果无向图 GGG 中任意两个顶点 uuu 和 vvv 之间是连通的,则称图 GGG 是连通图。
- 在有向图 GGG 中,如果对于任意两个顶点 uuu 和 vvv,从 uuu 到 vvv 和 从 vvv 到 uuu 都存在道路,则称图 GGG 是强连通图。
图的表示
1.关联矩阵
对于无向图,关联矩阵 M=(mij)n×m\boldsymbol{M}=\left(m_{i j}\right)_{n \times m}M=(mij)n×m:
mij={1,vi 与 ej 相关联, 0,vi 与 ej 不关联. m_{i j}=\left\{\begin{array}{ll} 1, & v_{i} \text { 与 } e_{j} \text { 相关联, } \\ 0, & v_{i} \text { 与 } e_{j} \text { 不关联. } \end{array}\right. mij={1,0,vi 与 ej 相关联, vi 与 ej 不关联.
对于有向图,关联矩阵 M=(mij)n×m\boldsymbol{M}=\left(m_{i j}\right)_{n \times m}M=(mij)n×m:
mij={1,vi 是 ej 的起点, −1,vi 是 ej 的终点, 0,vi 与 ej 不关联. m_{i j}=\left\{\begin{array}{ll} 1, & v_{i} \text { 是 } e_{j} \text { 的起点, } \\ -1, & v_{i} \text { 是 } e_{j} \text { 的终点, } \\ 0, & v_{i} \text { 与 } e_{j} \text { 不关联. } \end{array}\right. mij=⎩
⎨
⎧1,−1,0,vi 是 ej 的起点, vi 是 ej 的终点, vi 与 ej 不关联.
2.邻接矩阵
对于有向非赋权图,其邻接矩阵 W=(wij)n×n\boldsymbol{W}=\left(w_{i j}\right)_{n \times n}W=(wij)n×n:
wij={1,⟨vi,vj⟩∈A0,⟨vi,vj⟩∉A w_{i j}=\left\{\begin{array}{ll} 1, & \left\langle v_{i}, v_{j}\right\rangle \in A \\ 0, & \left\langle v_{i}, v_{j}\right\rangle \notin A \end{array}\right. wij={1,0,⟨vi,vj⟩∈A⟨vi,vj⟩∈/A
最大流问题
- 公路系统有车辆流、物资调配系统有物资流、金融系统有现金流,这些流问题都可归结为网络流问题,如何安排使流量最大,即最大流问题。
1.基本概念
- 网络上的流,是指定义为弧集合 AAA 上的一个函数 f={fij}={f(vi,vj)}f=\left\{f_{ij}\right\}=\left\{f(v_i,v_j)\right\}f={fij}={f(vi,vj)}, fijf_{ij}fij 为弧 (vi,vj)(v_i,v_j)(vi,vj) 上的流量。
- 满足下列条件的流 fff 称为可行流:
(1)容量限制条件:对每条弧 (vi,vj)∈A,0⩽fij⩽cij\left(v_{i}, v_{j}\right) \in A, 0 \leqslant f_{i j} \leqslant c_{i j}(vi,vj)∈A,0⩽fij⩽cij
(2)平衡条件:对于中间点,流出量=流入量,即对于每个 i(i≠s,t)i(i \neq s, t)i(i=s,t)有
∑j:(vi,vj)∈Afij−∑j:(vj,vi)∈Afji=0 \sum_{j:\left(v_{i}, v_{j}\right) \in A} f_{i j}-\sum_{j:\left(v_{j}, v_{i}\right) \in A} f_{j i}=0 j:(vi,vj)∈A∑fij−j:(vj,vi)∈A∑fji=0
最大流问题可以写为如下线性规划模型:
maxvs.t.{∑j:(vi,vj)∈Afij−∑j:(vj,vi)∈Afji={v,i=s−v,i=t0,i≠s,t0⩽fij⩽cij,∀(vi,vj)∈A \begin{array}{l} \max v \\ s.t.\left\{\begin{array}{ll} \sum_{j:\left(v_{i}, v_{j}\right) \in A} f_{i j}-\sum_{j:\left(v_{j}, v_{i}\right) \in A} f_{j i}=\left\{\begin{array}{ll} v, & i=s \\ -v, & i=t \\ 0, & i \neq s, t \end{array}\right.\\ 0 \leqslant f_{i j} \leqslant c_{i j} , \forall \left(v_{i}, v_{j}\right) \in A \end{array} \right. \end{array} maxvs.t.⎩ ⎨ ⎧∑j:(vi,vj)∈Afij−∑j:(vj,vi)∈Afji=⎩ ⎨ ⎧v,−v,0,i=si=ti=s,t0⩽fij⩽cij,∀(vi,vj)∈A
最小费用流问题
- 在许多实际问题中,还需要考虑网络上流的费用问题。例如,在运输问题中,人们总是希望在完成运输任务的同时,寻求一个使总的运输费用最小的运输方案。
- 设 bijb_{ij}bij 为弧上的单位费用,则最小费用流问题可用如下线性规划问题描述:
max∑(vi,vj)∈Abijfijs.t.{∑j:(vi,vj)∈Afij−∑j:(vj,vi)∈Afji={v,i=s−v,i=t0,i≠s,t0⩽fij⩽cij,∀(vi,vj)∈A \begin{array}{l} \max \sum_{(v_i,v_j)\in A}^{} b_{ij}f{ij} \\ s.t.\left\{\begin{array}{ll} \sum_{j:\left(v_{i}, v_{j}\right) \in A} f_{i j}-\sum_{j:\left(v_{j}, v_{i}\right) \in A} f_{j i}=\left\{\begin{array}{ll} v, & i=s \\ -v, & i=t \\ 0, & i \neq s, t \end{array}\right.\\ 0 \leqslant f_{i j} \leqslant c_{i j} , \forall \left(v_{i}, v_{j}\right) \in A \end{array} \right. \end{array} max∑(vi,vj)∈Abijfijs.t.⎩ ⎨ ⎧∑j:(vi,vj)∈Afij−∑j:(vj,vi)∈Afji=⎩ ⎨ ⎧v,−v,0,i=si=ti=s,t0⩽fij⩽cij,∀(vi,vj)∈A - 当 vvv 是最大流 vmaxv_{max}vmax 时,本问题就是最小费用最大流问题。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)