统计学习方法（李航）第五章决策树

笔记目录：统计学习方法（李航）第一章绪论统计学习方法（李航）第二章感知机统计学习方法（李航）第三章 k近邻统计学习方法（李航）第四章贝叶斯统计学习方法（李航）第五章决策树决策树是一种树形结构的分类或回归模型，通过一系列 if-then 规则对数据进行决策示例：对于数据集 {(x1,y1),(x2,y2),…,(xn,yn)}\{ (x_1, y_1), (x_2, y_2), \do

小海496

1274人浏览 · 2025-04-30 21:49:09

小海496 · 2025-04-30 21:49:09 发布

笔记目录：
统计学习方法（李航）第一章绪论
 统计学习方法（李航）第二章感知机
 统计学习方法（李航）第三章 k近邻
 统计学习方法（李航）第四章贝叶斯
 统计学习方法（李航）第五章决策树

第一节决策树介绍

1. 决策树的概念

决策树是一种树形结构的分类或回归模型，通过一系列 if-then 规则对数据进行决策

if-then 规则：每个节点表示一个条件（如“年龄 > 30？”），根据条件判断进入不同的子节点
互斥性：每个条件的结果（如“是”或“否”）对应唯一的分支，分支间互斥
完备性：所有可能的条件组合都被覆盖，确保每个输入都能被分类

示例：
对于数据集 $\{ (x_1, y_1), (x_2, y_2), \dots, (x_n, y_n) \}$ ，决策树通过条件划分特征空间，最终输出类别 $y$

以鸢尾花数据集为例:

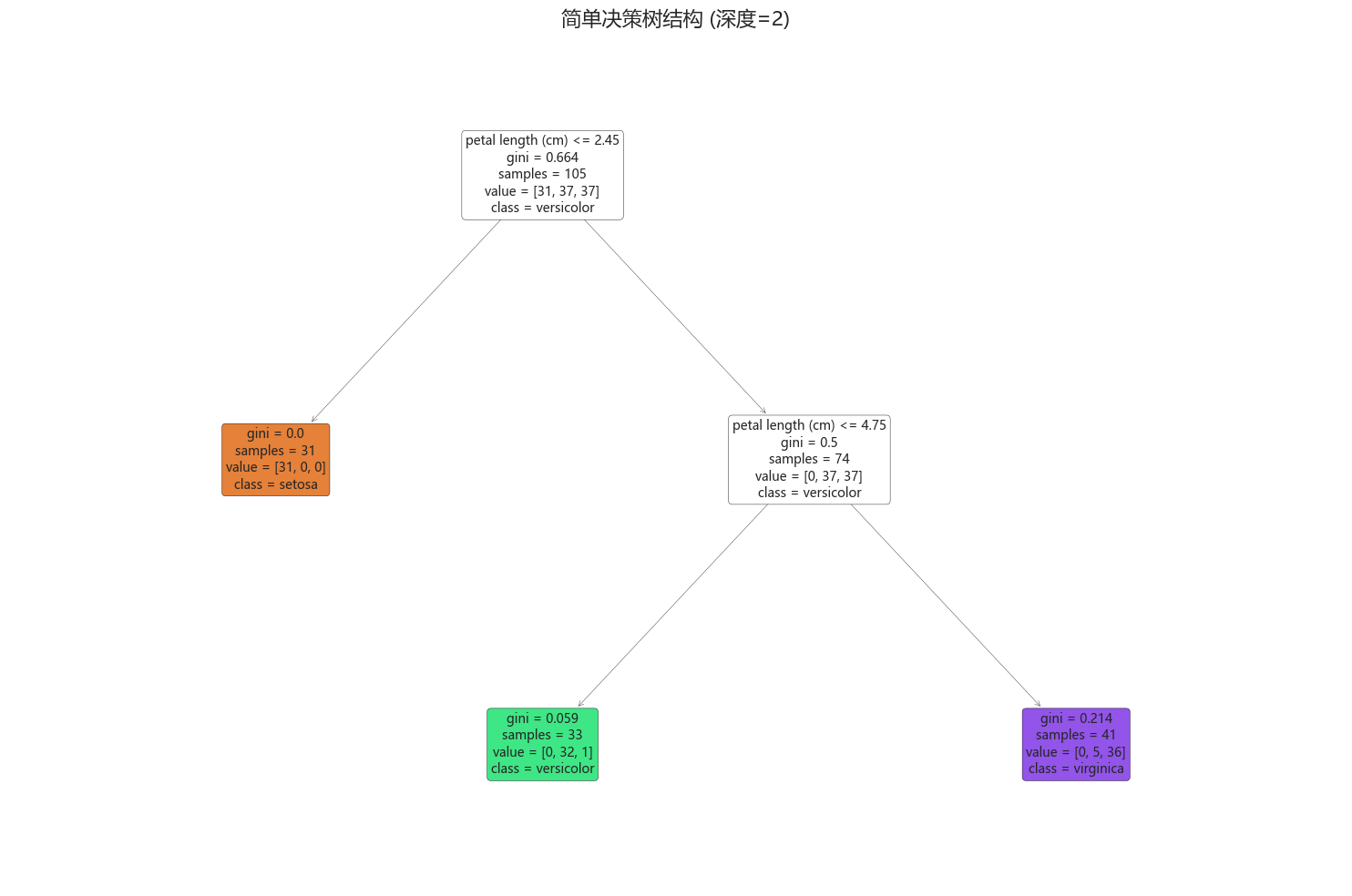
在这里插入图片描述

2. 构建决策树的基本过程

决策树的构建是一个递归过程，目标是选择 最优特征 划分数据集。基本步骤如下：

初始化：将整个数据集作为根节点
选择最优特征：
- 选择一个特征 $A$ （如“年龄”），根据其取值将数据集划分为若干子集
- 选择标准：划分后子集的“纯度”最高（即子集内的样本类别尽量一致）
递归划分：
- 对每个子集重复步骤 2，直到满足停止条件（例如子集纯度足够高或样本数少于阈值）
生成树：将所有划分结果组织成树形结构

数学表示：
假设特征 $A$ 有 $k$ 个取值 $\{ a_1, a_2, \dots, a_k \}$ ，数据集 $D$ 被划分为子集 $\{ D_1, D_2, \dots, D_k \}$ ，其中：

$D_i = \{ (x, y) \in D \mid x_A = a_i \}$

目标是选择使子集 ${ D_i \}$ 纯度最高的特征 $A$

3. 决策树与条件概率分布

决策树可以看作是对特征空间的划分，每个叶节点对应一个类别，隐含地表示条件概率分布

条件概率：对于特征向量 $x$ ，决策树通过路径到达叶节点，输出类别 $y$ ，即：

$P(\text{ 叶节点对应的类别} | x)$
划分特征空间：决策树将特征空间划分为互斥的区域，每个区域对应一个叶节点和类别

示例：
对于二维特征空间 $x_1, x_2)$ ，决策树可能划分为矩形区域，每个区域对应一个类别：

$\text{（如果 } x \text{ 落在类别 } c \text{ 的区域）}$

4. 决策树学习的基本概念

决策树学习的目标是构建一棵能够泛化良好的树。以下是相关概念：

本质：从训练数据中学习一组 if-then 规则，划分特征空间以预测类别
假设空间：所有可能的决策树集合，即不同特征组合和划分方式构成的树
策略：
- 选择最优特征进行划分
- 递归构建树，直到满足终止条件
特征选择：选择对分类任务贡献最大的特征（如基于纯度）
生成：从根节点开始，递归划分数据集，生成完整的决策树
剪枝：通过移除部分分支，简化树结构，防止过拟合
一棵好的决策树：
- 训练误差小：对训练数据的分类准确率高
- 泛化能力强：对未见过的数据有良好的预测能力
- 结构简单：树深度适中，避免过于复杂

数学目标：
决策树学习的目标是最小化损失函数（如分类误差）：

$L(\text{tree}) = \sum_{i=1}^n \mathbb{I}(y_i \neq \hat{y}_i)$

其中， $\mathbb{I}$ 为指示函数， $\hat{y}_i$ 为预测类别

第二节信息增益

1. 通过例子选择不同特征生成决策树

使用表格 5.1 数据，展示如何通过选择不同特征生成决策树，从而引出特征选择的重要性

表格 5.1 贷款申请样本数据表

ID	年龄	有工作	有自己房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	是	非常好	是
15	老年	否	否	一般	否

选择不同特征的决策树

若以“有工作”为根节点特征：
- 有工作 = 是：样本 {3, 4, 8, 13, 14}，类别全为“是”
- 有工作 = 否：样本 {1, 2, 5, 6, 7, 9, 10, 11, 12, 15}，类别混合（5 否，5 是）
若以“有自己房子”为根节点特征：
- 有自己房子 = 是：样本 {4, 8, 9, 10, 11, 12, 14}，类别全为“是”
- 有自己房子 = 否：样本 {1, 2, 3, 5, 6, 7, 13, 15}，类别混合（5 否，3 是）

结论：不同特征的选择会影响决策树的结构和划分效率。需要一个量化指标来选择最优特征

2. 信息增益（熵）

2.1 熵与不确定性

熵（Entropy）衡量数据集的不确定性，熵越大，不确定性越高。
对于类别集合 $Y$ ，假设有 $K$ 个类别，类别分布为 $\{ p_1, p_2, \dots, p_K \}$ ，熵定义为：

$\sum_{k=1}^K p_k \log_2 p_k$

证明等概率分布熵最大：
当 $p_1 = p_2 = \dots = p_K = \frac{1}{K}$ 时，熵最大
证明：使用拉格朗日乘数法，目标函数为 $\sum_{k=1}^K p_k \log_2 p_k$ ，约束 $\sum_{k=1}^K p_k = 1$ 。
引入拉格朗日函数：

$L(p_1, \dots, p_K, \lambda) = - \sum_{k=1}^K p_k \log_2 p_k + \lambda \left( \sum_{k=1}^K p_k - 1 \right)$

对 $p_k$ 求偏导：

$\frac{\partial L}{\partial p_k} = - \log_2 p_k - \frac{1}{\ln 2} + \lambda = 0 \implies \log_2 p_k = \lambda - \frac{1}{\ln 2}$

解得 $p_k = 2^{\lambda - \frac{1}{\ln 2}}$ ，由于 $\sum_{k=1}^K p_k = 1$ ，则 $p_k = \frac{1}{K}$
此时，熵为：

$\sum_{k=1}^K \frac{1}{K} \log_2 \frac{1}{K} = \log_2 K$

即等概率分布时熵最大

2.2 经验熵

经验熵是数据集 $D$ 的熵，反映数据集的类别分布
表格 5.1 中，类别“是”有 9 个，“否”有 6 个，总样本数 15

$\left( \frac{9}{15} \log_2 \frac{9}{15} + \frac{6}{15} \log_2 \frac{6}{15} \right) = - \left( 0.6 \log_2 0.6 + 0.4 \log_2 0.4 \right)$

计算： $\log_2 0.6 \approx -0.442$ , $\log_2 0.4 \approx -0.529$ ，则：

$\approx 0.971$

2.3 条件熵

条件熵 $H (D ∣ A)$ 表示在特征 $A$ 确定后，类别 $Y$ 的不确定性

$\sum_{i=1}^n \frac{|D_i|}{|D|} H(D_i)$

其中， $D_i$ 是特征 $A$ 取第 $i$ 个值时的子集

以“有工作”为例：

有工作 = 是： $D_1 = \{3, 4, 8, 13, 14\}$ ，5 个样本，全为“是”，熵 $H(D_1) = 0$
有工作 = 否： $D_2 = \{1, 2, 5, 6, 7, 9, 10, 11, 12, 15\}$ ，10 个样本（5 是，5 否），

熵：

$H(D_2) = - \left( \frac{5}{10} \log_2 \frac{5}{10} + \frac{5}{10} \log_2 \frac{5}{10} \right) = 1$

条件熵：

$H(D|\text{有工作}) = \frac{5}{15} \cdot 0 + \frac{10}{15} \cdot 1 = \frac{2}{3} \approx 0.667$

2.4 信息增益

信息增益衡量特征 $A$ 对数据集 $D$ 不确定性减少的程度：

$g (D, A) = H (D) - H (D ∣ A)$

其他特征：

“有自己房子”：有房子 = 是（7 是，0 否），熵 0；有房子 = 否（3 是，5 否），熵 0.954。条件熵：

$H(D|\text{有自己房子}) = \frac{7}{15} \cdot 0 + \frac{8}{15} \cdot 0.954 \approx 0.509, \quad g(D, \text{有自己房子}) = 0.971 - 0.509 = 0.462$

类似计算其他特征后，发现“有自己房子”信息增益最大，选择其为根节点

3. 信息增益比

信息增益可能偏向取值多的特征，信息增益比引入特征熵惩罚项：

$g_R(D, A) = \frac{g(D, A)}{H(A)}, \quad H(A) = - \sum_{i=1}^n \frac{|D_i|}{|D|} \log_2 \frac{|D_i|}{|D|}$

以“有工作”为例：

$H(\text{有工作}) = - \left( \frac{5}{15} \log_2 \frac{5}{15} + \frac{10}{15} \log_2 \frac{10}{15} \right) \approx 0.918$

$g_R(D, \text{有工作}) = \frac{0.304}{0.918} \approx 0.331$

类似计算其他特征，选择信息增益比最大的特征

第三节 ID3 与 C4.5 算法

1. ID3 算法

ID3 算法基于信息增益选择特征，递归构建决策树

算法步骤：

输入：训练数据集 $D$ ，特征集 $A$ ，阈值 $\epsilon$
输出：决策树 $T$

若 $D$ 中所有样本属于同一类 $C_k$ ，则置 $T$ 为单节点树，标记类 $C_k$ 为该节点的类别，返回 $T$
若 $\emptyset$ ，则置 $T$ 为单节点树，将 $D$ 中类别数最大的类 $C_k$ 标记为该节点的类别，返回 $T$
否则，按公式 (5.1) 计算 $A$ 中各特征对 $D$ 的信息增益，选择信息增益最大的特征 $A_g$ ：
$\quad A_g = \arg\max_{A \in A} g(D, A)$
若 $A_g$ 的信息增益小于阈值 $\epsilon$ ，则置 $T$ 为单节点树，将 $D$ 中类别数最大的类 $C_k$ 标记为该节点的类别，返回 $T$
否则，对 $A_g$ 的每个可能值 $a_i$ ，按 $A_g = a_i$ 将 $D$ 划分为子集 $D_i$ ，将 $D_i$ 中类别数最大的类 $C_k$ 标记为该子节点的类别，构建子节点，由节点及其子节点构成树 $T$ ，返回 $T$
对第 $i$ 个子节点，以 $D_i$ 为训练集，以 $A - \{A_g\}$ 为特征集，递归调用步骤 (1)~(5)，得到子树 $T_i$ ，返回 $T_i$

特点

ID3 使用信息增益作为特征选择标准，倾向于选择取值较多的特征
仅适用于离散特征，无法处理连续特征
不支持缺失值处理，需预处理数据

2. C4.5 算法

C4.5 是 ID3 的改进版本，使用信息增益比选择特征，支持连续特征和缺失值处理

算法步骤

输入：训练数据集 $D$ ，特征集 $A$ ，阈值 $\epsilon$
输出：决策树 $T$

若 $D$ 中所有样本属于同一类 $C_k$ ，则置 $T$ 为单节点树，标记类 $C_k$ 为该节点的类别，返回 $T$
若 $\emptyset$ ，则置 $T$ 为单节点树，将 $D$ 中类别数最大的类 $C_k$ 标记为该节点的类别，返回 $T$
否则，按公式 (5.10) 计算 $A$ 中各特征对 $D$ 的信息增益比，选择信息增益比最大的特征 $A_g$ ：

$g_R(D, A) = \frac{g(D, A)}{H(A)}, \quad A_g = \arg\max_{A \in A} g_R(D, A)$

其中， $\sum_{i=1}^n \frac{|D_i|}{|D|} \log_2 \frac{|D_i|}{|D|}$
若 $A_g$ 的信息增益比小于阈值 $\epsilon$ ，则置 $T$ 为单节点树，将 $D$ 中类别数最大的类 $C_k$ 标记为该节点的类别，返回 $T$
否则，对 $A_g$ 的每个可能值 $a_i$ ，按 $A_g = a_i$ 将 $D$ 划分为子集 $D_i$ 。若 $A_g$ 为连续特征，则按 $A_g \leq a_i$ 和 $A_g > a_i$ 划分；将 $D_i$ 中类别数最大的类 $C_k$ 标记为该子节点的类别，构建子节点，由节点及其子节点构成树 $T$ ，返回 $T$
对第 $i$ 个子节点，以 $D_i$ 为训练集，以 $A - \{A_g\}$ 为特征集，递归调用步骤 (1)~(5)，得到子树 $T_i$ ，返回 $T_i$

连续特征处理

C4.5 支持连续特征，方法是对连续特征 $A$ 排序后，选择划分点 $a$ ，将 $D$ 分为 $\leq a$ 和 $A > a$ 两部分
划分点选择：对连续特征值排序后，取相邻值的中点作为候选划分点，计算信息增益比，选择最大的划分点

缺失值处理

C4.5 引入概率权重处理缺失值：

对特征 $A$ ，计算无缺失值的样本比例 $w$
对无缺失值的样本，计算信息增益比 $g_R(D', A)$ ，调整为 $\cdot g_R(D', A)$
划分时，将缺失值样本按比例分配到各子节点

特点

使用信息增益比，减少对取值多特征的偏见
支持连续特征和缺失值处理，应用范围更广
引入剪枝策略（如悲观剪枝），提高泛化能力

ID3算法示例

以上一节使用的代换申请例子来进行ID3算法的实现：

第一步计算数据集 $D$ 的经验熵 $H (D)$

$\sum_{k=1}^K \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|}$

$∣ D ∣ = 15$ ，类别“是”：9，类别“否”：6
$\left( \frac{9}{15} \log_2 \frac{9}{15} + \frac{6}{15} \log_2 \frac{6}{15} \right)$
$\frac{9}{15} = 0.6$ ， $\frac{6}{15} = 0.4$
$\log_2 0.6 \approx -0.442$ ， $\log_2 0.4 \approx -0.529$
$H (D) = - (- 0.442 - 0.529) = 0.971$

第二步计算各特征的信息增益

特征集 $\{ \text{年龄}, \text{有工作}, \text{有自己房子}, \text{信贷情况} \}$
信息增益公式：

$\mid A), \quad H(D \mid A) = \sum_{i=1}^n \frac{|D_i|}{|D|} H(D_i)$

对于特征“有工作”:

有工作 = 是： $D_1 = \{3, 4, 8, 13, 14\}$ ，5 个样本，全为“是”， $H(D_1) = 0$
有工作 = 否： $D_2 = \{1, 2, 5, 6, 7, 9, 10, 11, 12, 15\}$ ，10 个样本（5 是，5 否）， $H(D_2) = - \left( \frac{5}{10} \log_2 \frac{5}{10} + \frac{5}{10} \log_2 \frac{5}{10} \right) = 1$
$\mid \text{有工作}) = \frac{5}{15} \cdot 0 + \frac{10}{15} \cdot 1 = 0.667$
$\text{有工作}) = 0.971 - 0.667 = 0.304$

对于特征“有自己房子”:

有自己房子 = 是： $D_1 = \{4, 8, 9, 10, 11, 12, 14\}$ ，7 个样本，全为“是”， $H(D_1) = 0$
有自己房子 = 否： $D_2 = \{1, 2, 3, 5, 6, 7, 13, 15\}$ ，8 个样本（3 是，5 否）， $H(D_2) = - \left( \frac{3}{8} \log_2 \frac{3}{8} + \frac{5}{8} \log_2 \frac{5}{8} \right) \approx 0.954$
$\mid \text{有自己房子}) = \frac{7}{15} \cdot 0 + \frac{8}{15} \cdot 0.954 \approx 0.509$
$\text{有自己房子}) = 0.971 - 0.509 = 0.462$

对于特征“年龄”:

年龄 = 青年： $D_1 = \{1, 2, 3, 4, 5\}$ ，5 个样本（2 是，3 否）， $H(D_1) = - \left( \frac{2}{5} \log_2 \frac{2}{5} + \frac{3}{5} \log_2 \frac{3}{5} \right) \approx 0.971$
年龄 = 中年： $D_2 = \{6, 7, 8, 9, 10\}$ ，5 个样本（3 是，2 否）， $H(D_2) \approx 0.971$
年龄 = 老年： $D_3 = \{11, 12, 13, 14, 15\}$ ，5 个样本（4 是，1 否）， $H(D_3) = - \left( \frac{4}{5} \log_2 \frac{4}{5} + \frac{1}{5} \log_2 \frac{1}{5} \right) \approx 0.722$
$\mid \text{年龄}) = \frac{5}{15} \cdot 0.971 + \frac{5}{15} \cdot 0.971 + \frac{5}{15} \cdot 0.722 \approx 0.888$
$\text{年龄}) = 0.971 - 0.888 = 0.083$

对于特征“信贷情况”:

信贷情况 = 一般： $D_1 = \{1, 4, 5, 6, 15\}$ ，5 个样本（1 是，4 否）， $H(D_1) \approx 0.722$
信贷情况 = 好： $D_2 = \{2, 3, 7, 8, 12, 13\}$ ，6 个样本（4 是，2 否）， $H(D_2) = - \left( \frac{4}{6} \log_2 \frac{4}{6} + \frac{2}{6} \log_2 \frac{2}{6} \right) \approx 0.918$
信贷情况 = 非常好： $D_3 = \{9, 10, 11, 14\}$ ，4 个样本，全为“是”， $H(D_3) = 0$
$\mid \text{信贷情况}) = \frac{5}{15} \cdot 0.722 + \frac{6}{15} \cdot 0.918 + \frac{4}{15} \cdot 0 \approx 0.608$
$\text{信贷情况}) = 0.971 - 0.608 = 0.363$

第三步选择最优特征

$\text{年龄}) = 0.083$
$\text{有工作}) = 0.304$
$\text{有自己房子}) = 0.462$
$\text{信贷情况}) = 0.363$

信息增益最大的特征是“有自己房子”（0.462），选择其为根节点

第四步递归划分

分支“有自己房子 = 是”

样本： $D_1 = \{4, 8, 9, 10, 11, 12, 14\}$ ，7 个样本，全为“是”
满足停止条件（所有样本同类），标记为叶节点，类别“是”

分支“有自己房子 = 否”

样本： $D_2 = \{1, 2, 3, 5, 6, 7, 13, 15\}$ ，8 个样本（3 是，5 否）
特征集更新： $\{ \text{年龄}, \text{有工作}, \text{信贷情况} \}$

计算 $H(D_2)$

$H(D_2) = - \left( \frac{3}{8} \log_2 \frac{3}{8} + \frac{5}{8} \log_2 \frac{5}{8} \right) \approx 0.954$

特征“有工作”

有工作 = 是： $D_{21} = \{3, 13\}$ ，2 个样本，全为“是”， $H(D_{21}) = 0$
有工作 = 否： $D_{22} = \{1, 2, 5, 6, 7, 15\}$ ，6 个样本，全为“否”， $H(D_{22}) = 0$
$H(D_2 \mid \text{有工作}) = \frac{2}{8} \cdot 0 + \frac{6}{8} \cdot 0 = 0$
$g(D_2, \text{有工作}) = 0.954 - 0 = 0.954$

信息增益为 0.954，远大于其他特征（此处可停止计算），选择“有工作”为子节点特征

有工作 = 是：叶节点，类别“是”
有工作 = 否：叶节点，类别“否”

当前决策树结构:

根节点：有自己房子
- 是：叶节点（类别“是”）
- 否：子节点（有工作）
  - 是：叶节点（类别“是”）
  - 否：叶节点（类别“否”）

第四节剪枝策略

1. 优秀的决策树与过拟合问题

优秀的决策树：

分类准确率高：对训练数据的分类误差小
泛化能力强：对未见数据（测试集）预测效果好
结构简单：树深度适中，避免过于复杂

过拟合问题：

决策树过深或节点过多，过度拟合训练数据
导致模型对训练数据表现良好，但对测试数据泛化能力差
示例：在贷款申请数据中，若决策树为每个样本生成一个分支，会完美拟合训练数据，但对新数据预测效果差

解决方法：通过剪枝策略简化决策树，提高泛化能力

2. 预剪枝策略

预剪枝在构建决策树时提前设置停止条件，限制树生长

2.1 限制深度

方法：设置决策树的最大深度 $L$ ，若树深度达到 $L$ ，停止划分
公式：无显式公式，深度计算为从根到叶的最长路径长度
示例：假设最大深度 $L = 1$ ，基于贷款数据（前节 ID3 结果）：
- 根节点选择“有自己房子”
- 深度达到 1，停止划分
- 有自己房子 = 是：类别“是”（7/7）
- 有自己房子 = 否：类别“否”（5 否，3 是，多数类为“否”）
- 结果：树只有根节点和两个叶节点，结构简单，但可能欠拟合

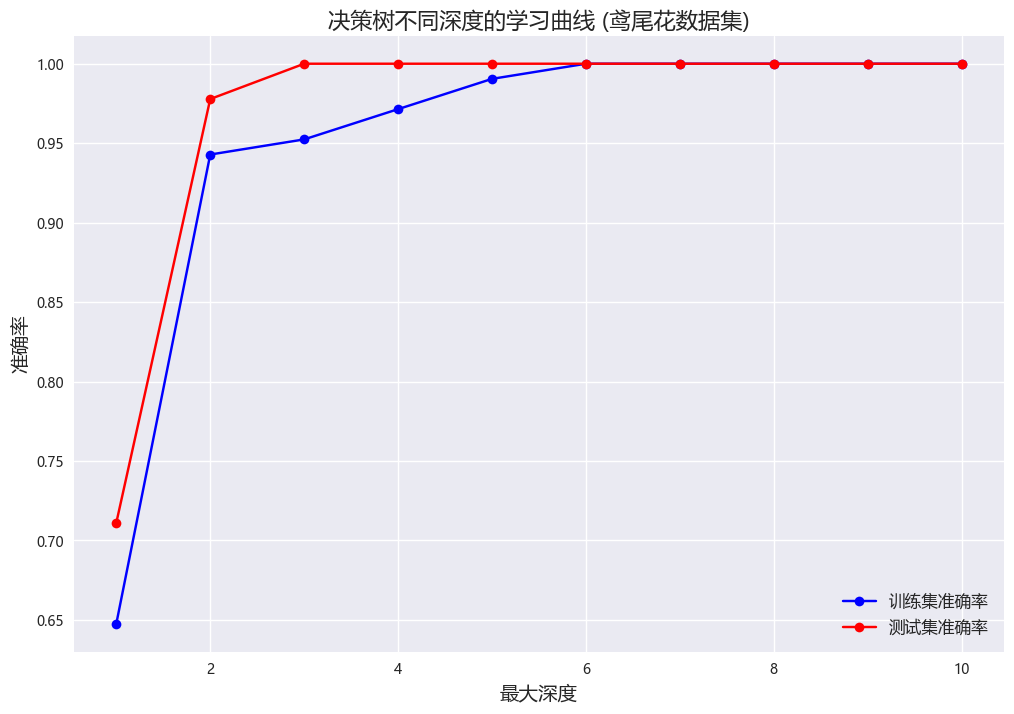
在这里插入图片描述

2.2 限制阈值

方法：设置信息增益阈值 $\epsilon$ ，若特征的信息增益小于 $\epsilon$ ，停止划分
公式：
$\mid A) < \epsilon$
示例：假设 $\epsilon = 0.5$ ，根节点信息增益计算（前节结果）：
- $\text{有自己房子}) = 0.462 < 0.5$ （实际为假，示例调整）。若 $g (D, A) < 0.5$ ，则停止划分，根节点直接标记为类别“是”（9 是，6 否）
- 结果：树退化为单节点，过于简单，可能欠拟合

2.3 基于测试集的误差率

方法：划分训练集和测试集，若继续划分后测试集误差率上升，则停止划分
公式：测试集误差率 $\frac{\text{测试集错误分类样本数}}{\text{测试集总样本数}}$
示例：假设测试集为样本 {3, 8, 15}（2 是，1 否），训练集为剩余样本
- 未划分：根节点标记为“是”（训练集 7 是，5 否）。测试集误差：样本 15 错误， $\frac{1}{3}$
- 划分（有自己房子）：
  - 是：{8}，类别“是”，正确
  - 否：{3, 15}，类别“否”（1 是，1 否），样本 3 错误， $\frac{1}{3}$ 。
- 误差率未降低，停止划分
- 结果：避免过深划分，但依赖测试集质量

3. 后剪枝策略

后剪枝在决策树生成后，通过移除部分分支简化树结构

3.1 基于降低测试集错误率

方法：自底向上，若剪枝后测试集错误率降低或不变，则剪枝
公式：剪枝前后测试集误差率变化： $\Delta E = E(T_{\text{剪枝前}}) - E(T_{\text{剪枝后}})$ ，若 $\Delta E \geq 0$ ，则剪枝
示例：使用前节 ID3 树，测试集 {3, 8, 15}：
- 剪枝前：
  - 样本 3：有自己房子 = 否，有工作 = 是，类别“是”，正确
  - 样本 8：有自己房子 = 是，类别“是”，正确
  - 样本 15：有自己房子 = 否，有工作 = 否，类别“否”，正确
  - $E(T_{\text{剪枝前}}) = 0$
- 剪枝“有工作”节点：有自己房子 = 否，类别“否”（其中3个是，5 否, 故预测类别为否）
  - 样本 3：类别“否”，错误
  - 样本 15：类别“否”，正确
  - $E(T_{\text{剪枝后}}) = \frac{1}{2}$
- $\Delta E = 0 - \frac{1}{2} < 0$ ，不剪枝
- 结果：保留分支，测试集误差更低

3.2 悲观错误剪枝（PEP）

方法：假设每个叶节点的错误分类服从二项分布，悲观估计错误率，若剪枝后悲观错误率降低，则剪枝
公式：叶节点错误率悲观估计： $\frac{e + 0.5}{N}$ （ $e$ 为错误样本数， $N$ 为样本数）。子树错误率： $\sum_{\text{叶节点}} \frac{N_i}{N} e(T_i)$ 。
示例：“有自己房子 = 否”子树：样本 {1, 2, 3, 5, 6, 7, 13, 15}（2个是，6个否）
- 剪枝前：
  - 有工作 = 是：{3, 13}，全“是”， $e(T_1) = \frac{0 + 0.5}{2} = 0.25$
  - 有工作 = 否：{1, 2, 5, 6, 7, 15}，全“否”， $e(T_2) = \frac{0 + 0.5}{6} \approx 0.083$
  - $\frac{2}{8} \cdot 0.25 + \frac{6}{8} \cdot 0.083 \approx 0.125$
- 剪枝后：类别“否”，错误 3 个， $\frac{3 + 0.5}{8} = 0.4375$
- $0.4375 > 0.125$ ，不剪枝
- 结果：悲观估计避免过度剪枝

3.3 最小误差剪枝（MEP）

方法：基于叶节点后验概率，计算期望误差，若剪枝后期望误差降低，则剪枝。
公式：叶节点期望误差： $e(T) = 1 - \max_k p(k|T)$ 。子树期望误差： $\sum_{\text{叶节点}} \frac{N_i}{N} e(T_i)$
示例：“有自己房子 = 否”子树：
- 剪枝前：
  - 有工作 = 是： $p(\text{是}) = 1$ ， $e(T_1) = 0$
  - 有工作 = 否： $p(\text{否}) = 1$ ， $e(T_2) = 0$
  - $E (T) = 0$
- 剪枝后： $p(\text{否}) = \frac{5}{8}$ ， $\frac{5}{8} = 0.375$
- $0.375 > 0$ ，不剪枝。
- 结果：保留子树，期望误差更低

3.4 基于错误剪枝（EBP）

方法：基于错误剪枝（Error-Based Pruning, EBP）通过公式 $U_\alpha(e(T), N(T))$ 计算剪枝后节点的悲观误差上界，若上界降低，则剪枝
公式： $U_\alpha(e(T), N(T)) = \frac{e(T) + 0.5 + \frac{q^2_\alpha}{2} + q_\alpha \sqrt{\frac{(e(T) + 0.5)(N(T) - e(T) - 0.5)}{N(T)} + \frac{q^2_\alpha}{4}}}{N(T) + q^2_\alpha}$
其中， $e (T)$ 为子树错误样本数， $N (T)$ 为子树样本总数， $q_\alpha$ 为置信度参数（如 $\alpha = 0.05$ 时， $q_\alpha \approx 1.96$ , 它是根据正态分布的置信度数据, 可通过线性插值拟合出来）
示例：“有自己房子 = 否”子树：样本 {1, 2, 3, 5, 6, 7, 13, 15}（2 个是，6 个否）
- 剪枝前：
  - 有工作 = 是：{3, 13}，全“是”， $e(T_1) = 0$ ， $N(T_1) = 2$ , $U_\alpha(0, 2) = \frac{0 + 0.5 + \frac{1.96^2}{2} + 1.96 \sqrt{\frac{(0 + 0.5)(2 - 0 - 0.5)}{2} + \frac{1.96^2}{4}}}{2 + 1.96^2}]$
    计算： $1.96^2 \approx 3.8416$ ， $\sqrt{\frac{0.5 \cdot 1.5}{2}} \approx 0.612$ ， $U_\alpha(0, 2) \approx \frac{0.5 + 1.9208 + 1.96 \cdot 0.612 + 0.9604}{5.8416} \approx 0.774$
  - 有工作 = 否：{1, 2, 5, 6, 7, 15}，全“否”， $e(T_2) = 0$ ， $N(T_2) = 6$ ， $U_\alpha(0, 6) \approx \frac{0.5 + 1.9208 + 1.96 \cdot \sqrt{\frac{0.5 \cdot 5.5}{6}} + 0.9604}{9.8416} \approx 0.380$
  - 总误差上界： $\frac{2}{8} \cdot 0.774 + \frac{6}{8} \cdot 0.380 \approx 0.479$
- 剪枝后：类别“否”， $e (T) = 3$ ， $N (T) = 8$ 。 $U_\alpha(3, 8) = \frac{3 + 0.5 + \frac{1.96^2}{2} + 1.96 \sqrt{\frac{(3 + 0.5)(8 - 3 - 0.5)}{8} + \frac{1.96^2}{4}}}{8 + 1.96^2}$
  计算： $\sqrt{\frac{3.5 \cdot 4.5}{8}} \approx 1.402$ ， $U_\alpha(3, 8) \approx \frac{3.5 + 1.9208 + 1.96 \cdot 1.402 + 0.9604}{11.8416} \approx 0.719$
- $0.719 > 0.479$ ，不剪枝
- 结果：保留子树，悲观误差上界更低

3.5 代价-复杂度剪枝（CCP）(下一节会详细介绍)

方法：引入复杂度惩罚，平衡误差和树复杂度，通过参数 $\alpha$ 选择最优子树。
公式：代价-复杂度： $C_\alpha(T) = E(T) + \alpha |T|$ ，其中 $E (T)$ 为训练集误差， $∣ T ∣$ 为叶节点数， $\alpha$ 为惩罚参数。对不同 $\alpha$ ，选择 $C_\alpha(T)$ 最小的子树
示例：基于贷款申请数据集的 ID3 决策树：
- 完整树 $T_1$ ：
  - 结构：根节点（有自己房子）→ 是（类别“是”），否 → 子节点（有工作）→ 是（类别“是”），否（类别“否”）
  - 训练集误差 $E(T_1) = 0$ （完全拟合）
  - 叶节点数 $T_1| = 3$
  - $C_\alpha(T_1) = 0 + \alpha \cdot 3 = 3\alpha$
- 剪枝子树 $T_2$ （剪去“有工作”节点）：
  - 结构：根节点（有自己房子）→ 是（类别“是”），否（类别“否”，多数类，2个是，6个否）
  - 训练集误差 $E(T_2) = 2$ （样本 3 和 13 错误）
  - 叶节点数 $T_2| = 2$
  - $C_\alpha(T_2) = 2 + \alpha \cdot 2 = 2 + 2\alpha$
- 剪枝子树 $T_3$ （剪去根节点，退化为单节点）：
  - 结构：单节点（类别“是”，9 是，6 否）
  - 训练集误差 $E(T_3) = 6$ （样本 1, 2, 5, 6, 7, 15 错误）
  - 叶节点数 $T_3| = 1$
  - $C_\alpha(T_3) = 6 + \alpha \cdot 1 = 6 + \alpha$
- 选择最优子树：
  - 比较 $T_1$ 和 $T_2$ ： $3\alpha < 2 + 2\alpha \implies \alpha < 2$ ， $\alpha < 2$ 时选 $T_1$
  - 比较 $T_2$ 和 $T_3$ ： $2\alpha < 6 + \alpha \implies \alpha < 4$ ， $\alpha < 4$ 时选 $T_2$
  - 综合：
    - $\alpha < 2$ ：选 $T_1$ （完整树）
    - $\leq \alpha < 4$ ：选 $T_2$ （剪去“有工作”）
    - $\alpha \geq 4$ ：选 $T_3$ （单节点）
- 结果：通过调整 $\alpha$ ，CCP 逐步简化树， $\alpha = 3$ 时选择 $T_2$ ，平衡了误差和复杂度

第五节 CART 算法

1. 基尼指数

基尼指数（Gini Index）用于衡量数据集的不确定性，值越小，数据集纯度越高。相比熵，基尼指数计算更简单，常用于 CART 算法

公式：对于数据集 $D$ ，有 $K$ 个类别，类别概率为 $\{ p_1, p_2, \dots, p_K \}$ ，基尼指数定义为：

$\text{Gini}(D) = 1 - \sum_{k=1}^K p_k^2$
- 当 $p_k = 1$ （数据集纯度最高）， $\text{Gini}(D) = 0$
- 当 $p_k = \frac{1}{K}$ （等概率分布，不确定性最大）， $\text{Gini}(D) = 1 - \frac{1}{K}$

条件基尼指数衡量特征 $A$ 划分后数据集的不确定性

公式：特征 $A$ 将数据集 $D$ 划分为子集 $\{ D_1, D_2, \dots, D_n \}$ ，条件基尼指数为：

$\text{Gini}(D|A) = \sum_{i=1}^n \frac{|D_i|}{|D|} \text{Gini}(D_i)$

CART 选择使 $\text{Gini}(D|A)$ 最小的特征和划分点
示例：贷款申请数据（15 个样本，9 是，6 否）：
- $\text{Gini}(D) = 1 - \left( \left(\frac{9}{15}\right)^2 + \left(\frac{6}{15}\right)^2 \right) = 1 - (0.36 + 0.16) = 0.48$
- 特征“有自己房子”：
  - 是：7 个样本（全“是”）， $\text{Gini}(D_1) = 1 - (1^2 + 0^2) = 0$
  - 否：8 个样本（2 是，6 否）， $\text{Gini}(D_2) = 1 - \left( \left(\frac{2}{8}\right)^2 + \left(\frac{6}{8}\right)^2 \right) = 1 - (0.0625 + 0.5625) = 0.625$
  - $\text{Gini}(D \mid \text{有自己房子}) = \frac{7}{15} \cdot 0 + \frac{8}{15} \cdot 0.625 \approx 0.33$

2. 分类树的生成

CART 分类树通过最小化基尼指数递归构建

算法步骤

输入：训练数据集 $D$ ，特征集 $A$
输出：分类树 $T$

若 $D$ 中样本同类或 $\emptyset$ ，标记为叶节点，返回 $T$
对每个特征 $A_i \in A$ 和其每个可能值 $a$ ：
- 若 $A_i$ 为离散特征，按 $A_i = a$ 和 $A_i \neq a$ 划分
- 若 $A_i$ 为连续特征，选划分点 $a$ ，按 $A_i \leq a$ 和 $A_i > a$ 划分
计算 $\text{Gini}(D \mid A_i)$ ，选择最小基尼指数的特征和划分点
按最优划分将 $D$ 分为子集，递归构建子树，返回 $T$

示例：贷款数据中，“有自己房子”基尼指数最小（0.33），选择为根节点。递归划分后，生成树：
- 根节点：有自己房子
  - 是：类别“是”
  - 否：子节点（有工作）
    - 是：类别“是”
    - 否：类别“否”

3. 回归树的生成

CART 回归树通过最小化平方误差构建

算法步骤

输入：训练数据集 $D$ ，特征集 $A$
输出：回归树 $T$

若 $D$ 样本数小于阈值或 $\emptyset$ ，标记为叶节点，输出值为样本均值，返回 $T$
对每个特征 $A_i$ 和划分点 $a$ ，按 $A_i \leq a$ 和 $A_i > a$ 划分 $D$ 为 $D_1$ 和 $D_2$
计算平方误差：

$\text{Error} = \sum_{x_i \in D_1} (y_i - \bar{y}_1)^2 + \sum_{x_i \in D_2} (y_i - \bar{y}_2)^2$

其中 $\bar{y}_1, \bar{y}_2$ 为子集均值
选择误差最小的特征和划分点，递归构建子树，返回 $T$

示例：
假设回归任务预测贷款金额，特征为“年龄”，值 {青年, 中年, 老年} 映射为 {1, 2, 3}，金额为 {10, 20, 30, …}。划分“年龄 $\leq 1.5$ ”，计算误差，选择最优划分

4. 剪枝策略

CART 使用代价-复杂度剪枝（CCP），通过引入参数 $\alpha$ 平衡树的误差和复杂度，生成最优子树序列 $\{T_0, T_1, \dots, T_n\}$

4.1 剪枝过程

公式

树的代价-复杂度：

$C_\alpha(T) = C(T) + \alpha |T|$

其中， $T$ 为子树， $C (T)$ 为训练误差（分类树为误分类数，回归树为平方误差）， $∣ T ∣$ 为叶节点数， $\alpha \geq 0$ 为复杂度参数。
节点 $t$ 的代价-复杂度：

$C_\alpha(t) = C(t) + \alpha$

其中， $C (t)$ 为节点 $t$ 的训练误差
子树 $T_t$ 的代价-复杂度：

$C_\alpha(T_t) = C(T_t) + \alpha |T_t|$

其中， $T_t$ 为以 $t$ 为根的子树
剪枝条件：

$C_\alpha(T_t) < C_\alpha(t)$

当 $\alpha$ 较小时， $C_\alpha(T_t) < C_\alpha(t)$ ，保留子树 $T_t$ ；当 $\alpha$ 较大时，剪枝为单节点 $t$
剪枝点 $\alpha$ 的计算：

$\alpha = \frac{C(t) - C(T_t)}{|T_t| - 1}$

其中， $T_t|$ 为子树 $T_t$ 的叶节点数
节点 $t$ 的 $g (t)$ 值：

$\frac{C(t) - C(T_t)}{|T_t| - 1}$

$g (t)$ 表示剪枝 $T_t$ 为 $t$ 时单位叶节点减少的误差，选择 $g (t)$ 最小的节点剪枝

算法步骤

初始化 $k = 0$ ， $T = T_0$ （完整树）
设 $\alpha = +\infty$
自底向上遍历内部节点 $t$ ，依次计算 $C(T_t)$ 、 $T_t|$ 和：
$\frac{C(t) - C(T_t)}{|T_t| - 1}, \quad \alpha = \min(\alpha, g(t))$
选择 $\alpha$ 的节点 $t$ ，剪枝 $T_t$ 为 $t$ , 根据多数表决投票得到树T
设 $k = k + 1$ ， $\alpha_k = \alpha$ ， $T_k = T$
若 $T_k$ 不是根结点(这里书上说的是根结点及两个叶子节点, 但是查阅其他资料后还是选择根结点)，返回步骤 3
生成子树序列 $\{T_0, T_1, \dots, T_n\}$

选择最优子树

从 $\{T_0, T_1, \dots, T_n\}$ 中选择最优子树 $T_\alpha$ ，通常通过验证集或交叉验证评估 $C(T_k)$ ，选择误差最小的 $T_k$

4.2 示例（简化的数据集）

假设我们有一个简化的分类数据集，包含 6 个样本，特征为“天气”（晴、阴）和“温度”（高、低），目标类别为“是否外出”（是、否）：

ID	天气	温度	是否外出
1	晴	高	是
2	晴	低	是
3	晴	高	否
4	阴	高	否
5	阴	低	是
6	阴	低	否

完整树 $T_0$ （CART 分类树）：
- 根节点：天气
  - 晴：{1, 2, 3} → 子节点（温度）
    - 高：{1, 3}（1 是，1 否，类别“是”，多数类），错误 1（样本 3）
    - 低：{2}（类别“是”），无错误
  - 阴：{4, 5, 6} → 子节点（温度）
    - 高：{4}（类别“否”），无错误
    - 低：{5, 6}（1 是，1 否，类别“是”，多数类），错误 1（样本 6）
- 训练误差 $C(T_0) = 1 + 1 = 2$ （样本 3 和 6 错误）
- 叶节点数 $T_0| = 4$
依次计算每个内部节点的 $g (t)$ ：
- 节点 $t_1$ （天气 = 晴下的温度节点）：
  - 子树 $T_{t_1}$ ：温度 → 高（1 是，1 否），低（1 是）
  - $C(T_{t_1}) = 1$ （样本 3 错误）， $T_{t_1}| = 2$
  - 剪枝为单节点：{1, 2, 3}（2 是，1 否，类别“是”）， $C(t_1) = 1$ （样本 3 错误）
  - $g(t_1) = \frac{C(t_1) - C(T_{t_1})}{|T_{t_1}| - 1} = \frac{1 - 1}{2 - 1} = 0$
- 节点 $t_2$ （天气 = 阴下的温度节点）：
  - 子树 $T_{t_2}$ ：温度 → 高（1 否），低（1 是，1 否）
  - $C(T_{t_2}) = 1$ （样本 6 错误）， $T_{t_2}| = 2$
  - 剪枝为单节点：{4, 5, 6}（1 是，2 否，类别“否”）， $C(t_2) = 1$ （样本 5 错误）
  - $g(t_2) = \frac{1 - 1}{2 - 1} = 0$
- 节点 $t_3$ （根节点：天气）：
  - 子树 $T_{t_3} = T_0$ ， $C(T_{t_3}) = 2$ ， $T_{t_3}| = 4$
  - 剪枝为单节点：{1, 2, 3, 4, 5, 6}（3 是，3 否，类别“是”）， $C(t_3) = 3$ （样本 3, 4, 6 错误）
  - $g(t_3) = \frac{3 - 2}{4 - 1} = \frac{1}{3}$
按照 $ \alpha$ 从小到大进行剪枝, 计算出 $C_\alpha(T)$ ：
- 初始： $\alpha = \min(0, 0, \frac{1}{3}) = 0$ ， $g(t_1) = g(t_2) = 0$ ，优先剪枝 $t_1$ ，生成 $T_1$ ：
  - 根节点：天气 → 晴（类别“是”），阴 → 子节点（温度）→ 高（类别“否”），低（类别“是”）。
  - $C(T_1) = 1 + 1 = 2$ ， $T_1| = 3$
- 继续： $\alpha = \min(0, \frac{1}{3}) = 0$ ，剪枝 $t_2$ ，生成 $T_2$ ：
  - 根节点：天气 → 晴（类别“是”），阴（类别“否”）
  - $C(T_2) = 1 + 1 = 2$ （晴：样本 3 错误；阴：样本 5 错误）， $T_2| = 2$
- 继续： $\alpha = \frac{1}{3}$ ，剪枝 $t_3$ ，生成 $T_3$ ：
  - 单节点：类别“是”
  - $C(T_3) = 3$ ， $T_3| = 1$
子树序列： ${T_0, T_1, T_2, T_3\}$ ，对应 $\alpha$ 区间 $\frac{1}{3}), [\frac{1}{3}, +\infty)$
最后根据验证机来选择最优子树：假设验证集 {1, 4}（1 是，1 否）：
- $T_0$ ：样本 1 正确，样本 4 正确，误差 0
- $T_1$ ：样本 1 正确，样本 4 正确，误差 0
- $T_2$ ：样本 1 正确，样本 4 正确，误差 0
- $T_3$ ：样本 1 正确，样本 4 错误，误差 1
选择 $T_2$ （误差 0 且树更简单， $\alpha \in [0, \frac{1}{3})$ ）
： $\alpha = \min(0, 0, \frac{1}{3}) = 0$ ， $g(t_1) = g(t_2) = 0$ ，优先剪枝 $t_1$ ，生成 $T_1$ ：
- 根节点：天气 → 晴（类别“是”），阴 → 子节点（温度）→ 高（类别“否”），低（类别“是”）。
- $C(T_1) = 1 + 1 = 2$ ， $T_1| = 3$
- 继续： $\alpha = \min(0, \frac{1}{3}) = 0$ ，剪枝 $t_2$ ，生成 $T_2$ ：
  - 根节点：天气 → 晴（类别“是”），阴（类别“否”）
  - $C(T_2) = 1 + 1 = 2$ （晴：样本 3 错误；阴：样本 5 错误）， $T_2| = 2$
- 继续： $\alpha = \frac{1}{3}$ ，剪枝 $t_3$ ，生成 $T_3$ ：
  - 单节点：类别“是”
  - $C(T_3) = 3$ ， $T_3| = 1$
子树序列： ${T_0, T_1, T_2, T_3\}$ ，对应 $\alpha$ 区间 $\frac{1}{3}), [\frac{1}{3}, +\infty)$
最后根据验证机来选择最优子树：假设验证集 {1, 4}（1 是，1 否）：
- $T_0$ ：样本 1 正确，样本 4 正确，误差 0
- $T_1$ ：样本 1 正确，样本 4 正确，误差 0
- $T_2$ ：样本 1 正确，样本 4 正确，误差 0
- $T_3$ ：样本 1 正确，样本 4 错误，误差 1
选择 $T_2$ （误差 0 且树更简单， $\alpha \in [0, \frac{1}{3})$ ）