描述性统计学是数据分析的基础内容,虽是基础,但是不能忽视,数据中最初展示的信息往往就是利用描述性统计学总结出来的。

描述性统计学回顾:

描述性统计学有五个重要的指标:

1,平均值 2,四分位数 3,标准差 4, 变异系数 5,标准分

1,平均值:平均值的统计学意义很简单,就是求一组数据的平均数:

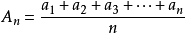
虽然平均数简单易求,也能反映出数据的一部分信息,但是,平均数对异常值的敏感度很低,比如在某些场景中:一群人的平均收入,如果其中某些人的收入比其他人高出几个数量级,其他人的平均收入也会被拉高,但并不能代表其他人的 收入也很高。

2,四分位数:四分位数有两个,一个是下四分位数为Q1,另一个是上四分位数Q3,他们的求法为:先对数据进行从大到小的排序,然后求出中位数Q2,此时用中位数将数据分为两部分,中位数左边的数据占总体数据的百分之五十,右边的数据也占总体数据的百分之五十,从左边百分之五十的数据中,找出这部分的中位数,该数据就是下四分位数,右边部分数据的中位数就是上四分位数。

同样四分位数能反应出一部分统计信息:能够从整体描述出数据集的分布状态,但是他也有一些缺点:无法描述数据的波动性。

利用四分位数,我们可以排除数据中的异常值,具体方法如下:

最小估计值:Q1-k(Q3-Q1)

最大估计值:Q3+k(Q3-Q1)

k=1.5时是中度异常,k=3时是极度异常,k越大,是异常值的可能性就越大。

3,标准差:标准差是用来衡量数据集的波动大小,标准差越大,说明数据的波动性越大。通常也会有其他的说法来表示数据集的波动大小:离散程度,变异性等

标准差的求法:

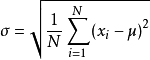
注意标准差的两个问题:1标准差的单位是什么?2标准差是大一点好,还是小一点好?

回答:1,标准差的单位根据具体的使用环境来确定,如果是用于工资环境,那么标准差的单位就是元,如果是用于求一个球员的能力的波动性,单位就是分。

2,标准差的大小,要根据使用的场景来确定,比如如果是求一个公司员工的收入的标准差,那么我们就期望标准差的值能大一点,因为不同职位不同的工作年限,薪资水平是肯定不同的,但是如果是求一个球员的得分能力的标准差,我们还是希望标准差可以小一点。

标准差也有一定的缺点,比如:如果两个数据差别比较大,那么就没法去衡量数据的波动大小,这里我们就要引入下面的概念。

4,变异系数:标准差能表示数据整体的波动，但是它有个缺点：如果两个数据差别比较大，那么就无法比较。

比如店铺A的销售额是1000万，店铺B的销售额是100万，两个店铺的标准差都是20万。如果说两个店铺的“波动幅度相同”，这是不对的。因为一般情况下，如果原始数据值较大，那么它的波动（标准差）也会比较大。这句话怎么理解呢？比如，20万对于1000万和100万的比例是不一样的，一个是五分之一，一个是五十分之一。
同样的标准差,对于不同量级的数据类型的意义是不同的。

如何避免标准差这个缺点呢？

如果能用标准差除以数据集的平均值，就可以消除数据大小的差异。标准差除以平均值得到的值叫作变异系数。

所以，我们通常用变异系数来比较不同数据集的波动大小。

5,标准分:标准分,也就是相对排名

它的计算公式为:

算出的标准分有以下几种情况:
等于0，等于平均值；大于零，大于平均值；小于零，小于平均值；