朴素贝叶斯分类方法的基本原理

1. 贝叶斯定理的回顾

贝叶斯定理（Bayes' Theorem）是统计学中一种非常重要的工具，它为我们提供了一种根据已知数据推断未知数据的方法。在机器学习中，贝叶斯定理被广泛应用于分类模型中。其数学公式为：

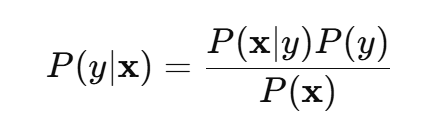
其中，公式中的各个部分代表了：

P(y∣x)：后验概率，即在观察到输入数据 x 后，属于类别 y 的概率。

P(x∣y)：似然函数，表示在类别 y下，观察到数据 x的概率。

P(y)：先验概率，表示在没有观察到 x 的情况下，类别 y 的概率。

P(x)：证据，也就是输入数据的总概率。这个值在求解时常常会被省略，因为它对于后验概率的大小比较没有影响（它对所有类别是常数）。

贝叶斯定理的核心思想是：通过已知的先验信息 P(y)P(y)P(y) 和观察到的数据 x\mathbf{x}x 来更新我们的信念，从而推断出在给定数据情况下，某个类别 yyy 的可能性（即后验概率）。

---

 2. 朴素贝叶斯假设

朴素贝叶斯分类器的关键假设是 特征条件独立性假设。也就是说，朴素贝叶斯假设所有特征 x1,x2,…,xn, ​ 在给定类别 y 的条件下是相互独立的。这个假设显著简化了计算，使得模型能够在有限的计算资源下高效地进行训练和预测。

在贝叶斯定理中，我们有：

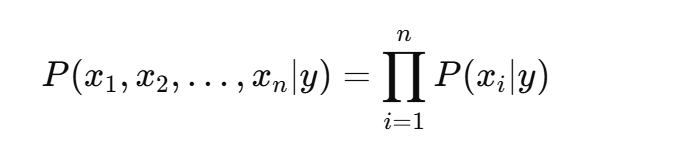
由于假设特征条件独立性，这个条件概率 P(x1,x2,…,xn∣y)可以拆解为：

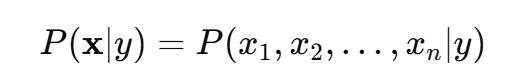
这意味着，我们不需要计算多个特征联合出现的复杂概率，而是可以将每个特征独立计算，然后将它们的概率相乘。这样，计算量大大减少。

例子：

假设我们要根据一组特征（如身高、体重、年龄等）来预测一个人的疾病类别。朴素贝叶斯假设这些特征在给定疾病类别的条件下是独立的.这样，特征之间的相关性就被忽略了，计算变得简单。

3. 朴素贝叶斯分类决策规则

在朴素贝叶斯中，我们的目标是 根据输入数据 x=(x1,x2,…,xn) 来预测类别 y。根据贝叶斯定理，我们通过计算每个类别 yyy 的后验概率来决定最有可能的类别。

首先，贝叶斯定理给出的后验概率是：

​

我们关心的是哪个类别的后验概率最大，因此，决策规则是选择使得 最大的类别 yyy：

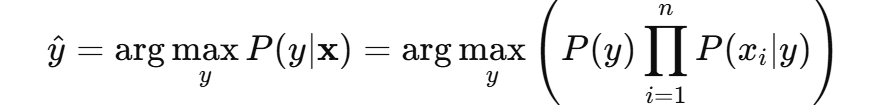
因为 P(x)P(\mathbf{x})P(x) 对所有类别是常数，通常我们会忽略它，从而简化为：

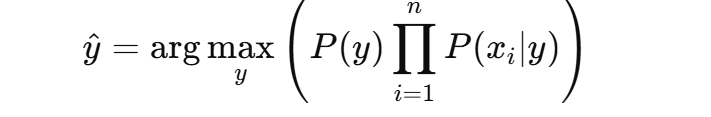
更进一步，通常我们使用 对数 形式来避免数值溢出：

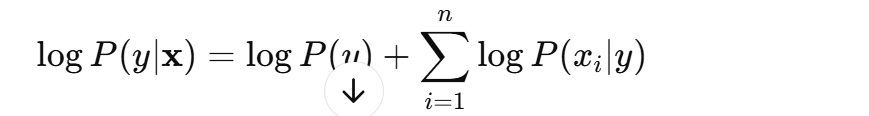
然后，选择对数后验概率最大的类别作为预测结果：

---

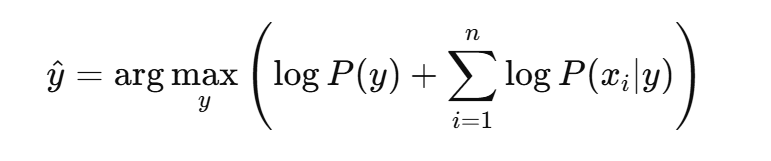
 4. 朴素贝叶斯的优点

朴素贝叶斯模型有以下几个优点：

计算简单：由于条件独立性假设，计算量较小，适合处理大规模数据集。

效率高：训练过程简单，只需要估计先验概率和特征条件概率，因此训练时间短。

良好的性能：即使特征之间有一定的相关性，朴素贝叶斯在许多实际应用中仍然能取得不错的结果，尤其是在 文本分类 和 垃圾邮件过滤 等问题中表现尤为出色。

---

 5. 朴素贝叶斯的缺点

朴素贝叶斯的缺点主要有：

特征独立性假设过于简单：很多现实中的问题，特征之间并非完全独立，朴素贝叶斯可能无法捕捉到这种依赖关系，导致分类性能下降。

对于特征之间有较强相关性的情况效果差：例如，在图像分类、语音识别等领域，特征之间可能存在较强的依赖关系，这时朴素贝叶斯的效果就会大打折扣。

无法处理特征之间的交互信息：在一些需要捕捉特征之间复杂关系的任务中，朴素贝叶斯可能无法得到良好的效果。

 朴素贝叶斯分类器的训练与参数估计

1. 训练朴素贝叶斯分类器的目标

朴素贝叶斯分类器是通过基于训练数据的 概率推断 来预测新样本的类别。目标是通过学习训练数据中每个类别的 先验概率 和每个特征的 条件概率 来构建模型。

2. 先验概率的估计

先验概率P(y)：

• 先验概率 是指在没有任何特征输入的情况下，某个类别 y 出现的概率。它是基于训练数据中每个类别的频率进行估计的。

• 设训练集 D={(x1,y1),(x2,y2),…,(xm,ym)}，其中 xi 是输入特征，yi​ 是类别标签。类别 y 的先验概率 P(y)就是类别 y在所有样本中出现的频率，即：

具体计算：如果有 n 个样本，其中有 nyn​ 个样本属于类别 y，则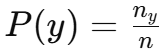 

这个先验概率 P(y) 的计算很简单，主要基于训练集中各个类别的频率。

---

3. 条件概率的估计

条件概率 P(xi∣y)：

• 条件概率 P(xi∣y) 是在已知类别 y 的情况下，特征 xi的值出现的概率。朴素贝叶斯假设 特征独立，即各个特征在类别 y 给定的情况下是条件独立的。因此，模型只需要估计每个特征 xi 在类别 yy下的条件概率 P(xi∣y)

• 离散特征：假设每个特征是离散的（例如颜色、形状等类别变量），我们可以通过统计每个特征值在各个类别下出现的频率来估计条件概率。对于特征 xi和类别 y，条件概率可以表示为：

示例：如果我们在训练集中观察到，在类别 y1​ 下，特征 x1​ 的取值为 a1​ 的样本有 5 个，而类别 y1 的样本总数为 20 个，那么 P(x1=a1∣y1)=520=0.25

• 连续特征：假设特征是连续型的（例如体重、身高等），通常我们假设特征在各类别下服从 正态分布（高斯分布）。在这种情况下，我们需要估计每个特征的均值和方差，然后通过正态分布公式来计算条件概率。

如果特征 xi 在类别 y 下服从正态分布，则条件概率 P(xi∣y) 为：

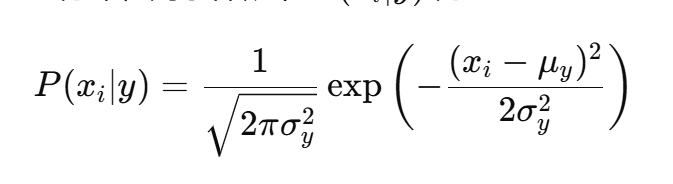
其中，μy​ 是类别 y下特征 xi​ 的均值，σ是类别 y 下特征 xi 的方差。

4. 平滑方法（避免零概率问题）

在实际应用中，特别是当特征是离散型时，某些特征值在训练集中的某些类别下可能没有出现过。这会导致条件概率为零，而这种零概率会影响到模型的预测。为了避免这个问题，我们使用 平滑技术。

拉普拉斯平滑（Laplace Smoothing）：

• 拉普拉斯平滑 主要用于避免在估计条件概率时出现零概率问题。在没有出现的情况下，通过增加一个小的常数来调整概率的估计。

对于离散特征 xix_ixi​ 和类别 yyy，使用拉普拉斯平滑后的条件概率计算公式为：

这里的“+1”是对未出现过的特征值进行平滑，使得即使某个特征在某类别下未出现过，也能有一个非零的概率。

---

5. 参数估计总结

• 先验概率 P(y)：通过计算每个类别在训练数据中的频率来估计。它反映了在没有任何特征信息的情况下，样本属于某一类别的可能性。

• 条件概率 P(xi∣y)：对于离散特征，通过统计特征值在每个类别中的频率来估计；对于连续特征，假设特征服从高斯分布，通过估计均值和方差来计算。

• 平滑方法：为了避免某些特征值在某些类别中未出现过而导致的零概率问题，使用拉普拉斯平滑。

---

6. 训练朴素贝叶斯模型的步骤

1. 计算先验概率 P(y)：基于训练数据中的类别频率计算。

2. 计算条件概率 P(xi∣y)：对于离散特征，计算其在各类别中的频率；对于连续特征，假设服从高斯分布，计算均值和方差。

3. 应用平滑方法：确保计算的条件概率不会为零，避免零概率问题。

4. 构建模型：将估计的先验概率和条件概率代入贝叶斯定理，用于预测新的样本类别。

---

7. 总结

• 训练过程：朴素贝叶斯模型的训练过程是通过最大似然估计（MLE）计算先验概率和条件概率，训练过程相对简单，计算效率高。

• 特征独立假设：朴素贝叶斯假设特征是条件独立的，因此它适用于高维数据（如文本数据）。

• 平滑技术：为了避免零概率问题，通常会使用拉普拉斯平滑或其他平滑方法。

• 朴素贝叶斯的优势：训练和预测的时间复杂度低，特别适用于大规模数据集，尤其是在文本分类等任务中表现良好。

贝叶斯分类器的决策规则 

1. 贝叶斯决策规则

贝叶斯分类器的决策规则是基于 后验概率 来进行的，即我们在已知某些特征的情况下，选择使后验概率最大的类别。贝叶斯分类器使用的是 最大后验估计（MAP估计）。

后验概率的公式：

根据贝叶斯定理，后验概率 P(y∣x) 可以表示为：

• P(y∣x)：给定特征 xx后，样本属于类别 yy的后验概率。

• P(x∣y))：给定类别 y，样本的特征 x 的条件概率。

• P(y)：类别 y的先验概率。

• P(x))：特征 x 的边际概率，通常作为常数来规范化。

2. 最大后验概率决策

贝叶斯分类器的决策规则是选择使后验概率最大的类别，即：

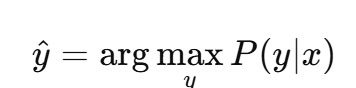
由于 P(x)P(x)P(x) 是与类别 yyy 无关的常数，我们可以忽略它。于是，贝叶斯分类器的决策规则简化为：

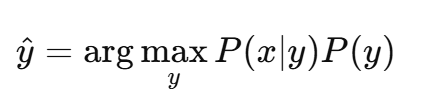
即，对于每一个类别 y，计算其 条件概率 P(x∣y) 和 先验概率 P(y) 的乘积，选择使这个乘积最大的类别作为最终的预测结果。

---

3. 条件独立性假设的应用

朴素贝叶斯的核心假设是 条件独立性假设，即假设给定类别 yyy 后，特征之间是独立的。因此，贝叶斯分类器可以将 联合条件概率 P(x∣y) 分解为各个特征条件概率的乘积：

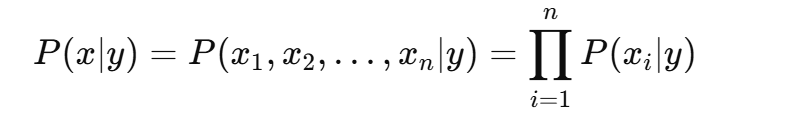
所以，在实际应用中，我们用 条件独立性假设 来简化模型计算。此时，贝叶斯分类器的决策规则变为：

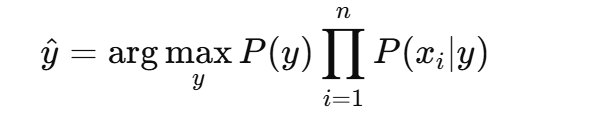
这个公式表明，给定一个样本 x=(x1,x2,…,xn)，我们通过计算每个类别 yyy 下的先验概率 P(y) 以及每个特征 xi在该类别下的条件概率 P(xi∣y)，再将它们相乘并选择最大值对应的类别。

---

4. 最大化后验概率的过程

在实际中，为了选择最可能的类别，我们计算后验概率 P(y∣x)，并选择其值最大的类别。贝叶斯分类器的决策过程就是通过最大化后验概率来实现的。

假设我们有一个训练集 D={(x1,y1),(x2,y2),…,(xm,ym)}，其中 xi 是特征向量，yi​ 是类别标签。在训练过程中，我们已经估计了每个类别的先验概率 P(y) 和每个特征在各类别下的条件概率 P(xi∣y)

决策步骤：

1. 计算每个类别的后验概率：对于新样本 x=(x1,x2,…,xn)，计算每个类别 yyy 的后验概率 P(y∣x)。

   

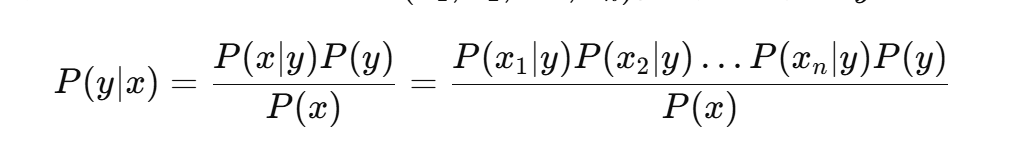
   由于 P(x) 对所有类别都相同，可以忽略它。因此我们只需计算：

   

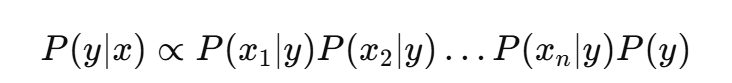
2. 选择最大后验概率对应的类别：选择使后验概率 P(y∣x) 最大的类别 y，即：

   

---

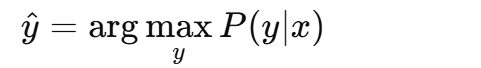
5. 贝叶斯分类器的预测过程

• 输入：一组特征向量 x=(x1,x2,…,xn)。

• 计算后验概率：使用最大后验概率决策规则，计算每个类别 yyy 的后验概率 P(y∣x)。

• 选择类别：选择后验概率最大的类别作为预测结果 y^​。

在实际应用中，这个过程可以通过以下步骤来实现：

1. 对每个类别 y，计算其先验概率 P(y)。

2. 对每个特征 xi​，计算其在类别 y 下的条件概率 P(xi∣y)。

3. 将条件概率和先验概率相乘，得到每个类别的联合概率。

4. 选择最大联合概率对应的类别作为预测类别。

---

6. 总结

贝叶斯分类器的决策规则核心在于通过 后验概率 来选择类别。最大后验概率决策规则通过 先验概率 和 条件概率 的乘积来进行类别预测。条件独立性假设使得朴素贝叶斯分类器的计算变得简单高效，适用于高维数据集，尤其在文本分类等任务中表现突出。

贝叶斯分类器的学习和预测过程简单、直观，并且可以根据数据集的大小和特征类型进行灵活的调整。通过最大后验估计（MAP），贝叶斯分类器能够为每个样本选择最可能的类别。